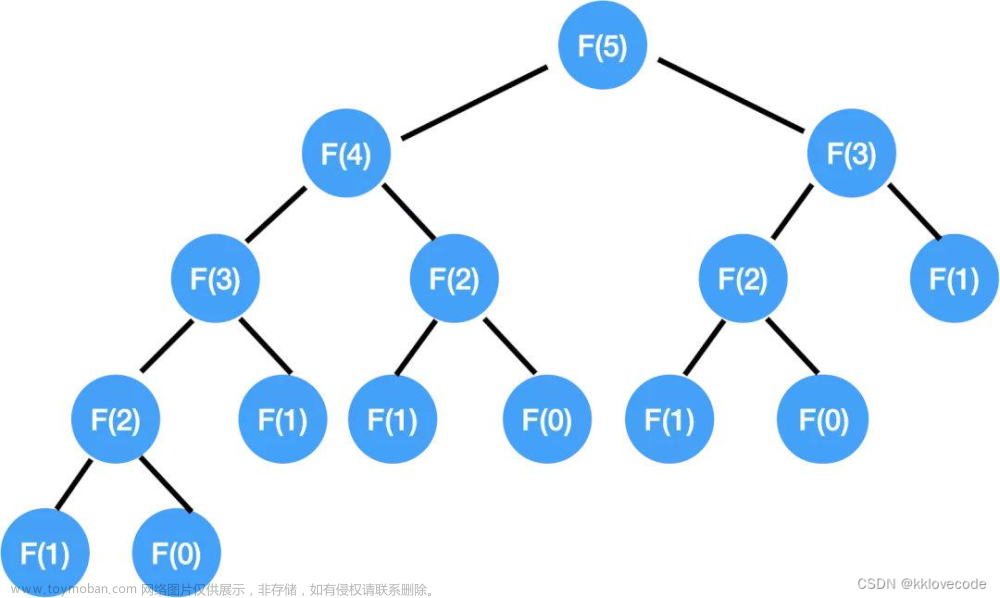
一、递归详解
[1] 递归是一种编程技巧,通过函数调用自身来解决问题。递归中包含三个要素:递归定义、递归出口和递归调用。
[2] 递归定义指的是问题可以被分解为同类且更小规模的子问题。在递归过程中,问题会不断被分解为规模更小的子问题,直到达到一个基本情况,该基本情况可以被直接求解,而无需再进行递归调用。
[3] 递归出口是指基本情况的判断条件。如果满足基本情况,递归函数将直接返回结果,否则将继续进行递归调用。
[4] 递归调用是指在函数内部调用该函数本身的过程。递归调用会使得函数的调用栈不断增长,直到达到系统设定的最大栈深度或者发生栈溢出等异常情况。
[5] 递归可以让我们更清晰地理解某些问题的解法,但也有可能会导致性能问题或栈溢出等风险。在使用递归时需要注意控制递归深度和对递归出口的正确处理。
[6] 常见的递归算法包括斐波那契数列、二叉树遍历、汉诺塔问题等。使用递归时需要注意分析算法的时间复杂度和空间复杂度,避免出现性能瓶颈或内存不足等情况。
二、下面是一个使用递归计算斐波那契数列的C语言例程:
#include <stdio.h>
int fibonacci(int n) {
if (n <= 1)
return n;
else
return fibonacci(n-1) + fibonacci(n-2);
}
int main() {
int n = 10;
printf("斐波那契数列前%d项为:\n", n);
for (int i = 0; i < n; i++) {
printf("%d ", fibonacci(i));
}
printf("\n");
return 0;
}在上述代码中,我们使用递归的方式计算斐波那契数列的第n项。在递归函数fibonacci中,如果n小于等于1,我们直接返回n本身;否则,递归计算第n-1项和第n-2项的值,并将它们相加返回。递归过程会一直持续到计算到第1项或第0项,然后一步步返回到主函数中输出结果。
需要注意的是,使用递归计算斐波那契数列时,由于递归调用的次数会随着n的增大而指数级增加,所以可能会导致性能问题或栈溢出等风险。因此,在实际使用时需要适当控制递归深度和对递归出口的正确处理。
三、二叉树遍历c语言递归例程
下面是一个使用递归遍历二叉树的C语言例程,包括先序遍历(preorder)、中序遍历(inorder)和后序遍历(postorder)三种方式:
#include <stdio.h>
#include <stdlib.h>
// 二叉树节点信息
struct binarytreenode {
int data;
struct binarytreenode *lchild; //左子树
struct binarytreenode *rchild; //右子树
};
// 先序遍历
void preorder(struct binarytreenode *root) {
if (root == NULL) {
return;
}
printf("%d ", root->data);
preorder(root->lchild);
preorder(root->rchild);
}
// 中序遍历
void inorder(struct binarytreenode *root) {
if (root == NULL) {
return;
}
inorder(root->lchild);
printf("%d ", root->data);
inorder(root->rchild);
}
// 后序遍历
void postorder(struct binarytreenode *root) {
if (root == NULL) {
return;
}
postorder(root->lchild);
postorder(root->rchild);
printf("%d ", root->data);
}
// 创建二叉树节点
struct binarytreenode *createbinarytreenode(int data) {
struct binarytreenode *p = (struct binarytreenode *)malloc(sizeof(struct binarytreenode));
p->data = data;
p->lchild = NULL;
p->rchild = NULL;
return p;
}
int main() {
struct binarytreenode *root = createbinarytreenode(1);
root->lchild = createbinarytreenode(2);
root->rchild = createbinarytreenode(3);
root->lchild->lchild = createbinarytreenode(4);
root->lchild->rchild = createbinarytreenode(5);
root->rchild->lchild = createbinarytreenode(6);
root->rchild->rchild = createbinarytreenode(7);
printf("先序遍历结果为: ");
preorder(root);
printf("\n");
printf("中序遍历结果为: ");
inorder(root);
printf("\n");
printf("后序遍历结果为: ");
postorder(root);
printf("\n");
return 0;
}
在上述代码中,我们首先定义了一个二叉树节点结构体binarytreenode,包括节点值data、左子树指针lchild和右子树指针rchild三个成员。然后定义了先序遍历(preorder)、中序遍历(inorder)和后序遍历(postorder)三个函数,分别用递归的方式遍历二叉树的每个节点,并按照遍历顺序输出节点值。
在主函数中,我们手动创建了一个7个节点的二叉树,并依次调用三种遍历函数。需要注意的是,在使用递归遍历二叉树时,需要判断当前节点是否为空,如果为空则直接返回;否则按照对应遍历顺序先递归遍历左子树,再输出当前节点值,最后递归遍历右子树。
四、汉诺塔问题c语言递归例程
下面是汉诺塔问题的C语言递归例程实现:
#include <stdio.h>
// 将n个盘子从from柱子借助by柱子移动到to柱子
void move(int n, char from, char by, char to) {
if (n == 1) { // 只有一个盘子时,直接移动到to柱子上
printf("Move disk %d from %c to %c\n", n, from, to);
} else { // 将n-1个盘子从from柱子借助to柱子移动到by柱子
move(n-1, from, to, by);
printf("Move disk %d from %c to %c\n", n, from, to);
// 将n-1个盘子从by柱子借助from柱子移动到to柱子
move(n-1, by, from, to);
}
}
int main() {
int n = 3; // 汉诺塔的圆盘数
char A = 'A', B = 'B', C = 'C'; // 三根柱子的名称
move(n, A, B, C); // 将n个盘子从A柱子借助B柱子移动到C柱子
return 0;
}
在上述代码中,我们定义了一个函数move,用于将n个盘子从from柱子借助by柱子移动到to柱子。在该函数中,我们首先判断当前移动的盘子数是否为1,如果是,则直接将该盘子从from柱子移动到to柱子;否则,将n-1个盘子从from柱子借助to柱子移动到by柱子,再将第n个盘子从from柱子移动到to柱子,最后将n-1个盘子从by柱子借助from柱子移动到to柱子。在每次移动时,都输出移动的盘子编号以及移动的来源柱子和目标柱子。文章来源:https://www.toymoban.com/news/detail-474113.html
在主函数中,我们定义了汉诺塔的圆盘数n和三根柱子的名称A、B、C,并调用move函数将n个盘子从A柱子借助B柱子移动到C柱子。文章来源地址https://www.toymoban.com/news/detail-474113.html
到了这里,关于递归详解,斐波那契数列、二叉树遍历、汉诺塔问题的递归代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!