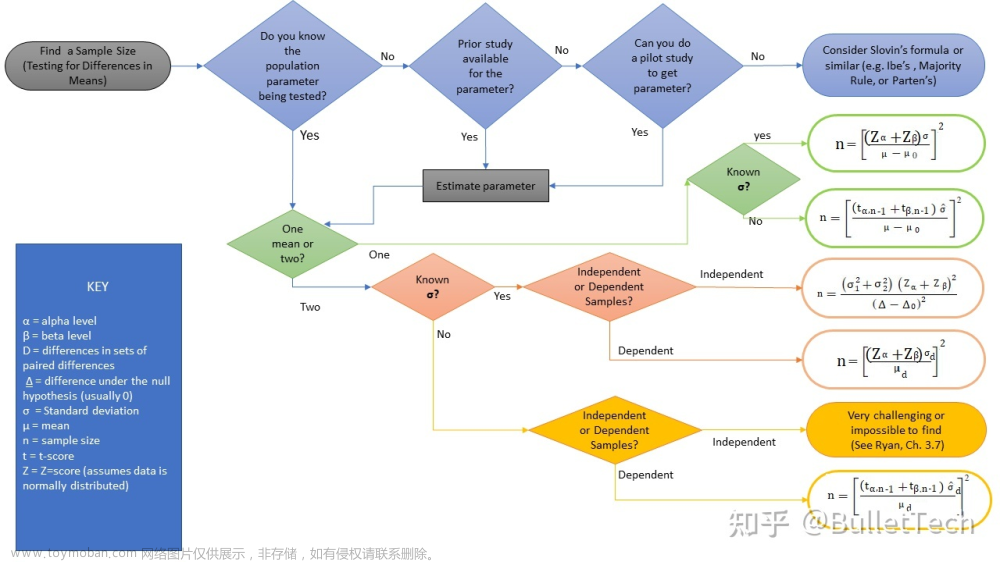
异常值检验
T-test
参考:1.ttest和ttest2 区别
2. ttest在 matlab
3.T test分布表 单侧
方差分析(ANOVA)
Def: 方差分析(analysis of variance, ANOVA)是一种统计检验,用于检验两组或更多组样本的均值是否相同。
与T test区别:
方差分析能够在不增加第一类错误发生率的情况下测试几组样本均值之间是否存在差异。
1.方差分析按影响分析指标的因素(也可简单成为
自变量)个数的多少,分为单因素方差分析(one-way ANOVA)、双因素方差分析、三因素方差分析 (两个或多个因素,称为多因素方差分析,multi-way ANOVA)。
2.按分析指标(也可简单称为因变量)的个数多少,分为一元方差分析(即ANOVOA)、多元方差分析(即,MANOVOA)。
方差齐性,也即方差分析是针对方 差一致的情况下,检验样本均值是否一致。
结论:p值均大于0.05,任意两组之间不存在显著差异。
p值均>0.05,说明在显著性水平0.05下均接受原假设,即服从正态分布。
p值均<给定的显著性水平0.05,所以可以认为氮、磷两种肥料的施用量对水稻的产量均有显著性影响,并且他们之间的交互作用也是非常显著的。
isvarname(x)文章来源:https://www.toymoban.com/news/detail-474471.html
1.方差分析 全文章来源地址https://www.toymoban.com/news/detail-474471.html
到了这里,关于异常值检验(t分布查表)、方差分析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!