1. Toy模板网首页
  2. > Toy博客

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

9月前 作者：陈亦康 分类：Toy博客 阅读(48) 违法举报

这篇具有很好参考价值的文章主要介绍了【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

目录

前言

一、图

1.1、基本概念

二、图的存储结构

2.1、存储结构

2.1、邻接矩阵（考察重点）

2.1.1、代码实现

2.2、邻接表

2.3.1、无向邻接表存储

2.3.2、有向图邻接表存储

3.1、图的广度优先遍历（层序遍历）

3.2、图的深度优先遍历

前言

本章主要讲的是图的基本概念以及应用，面试的时候基本不考图~

一、图

1.1、基本概念

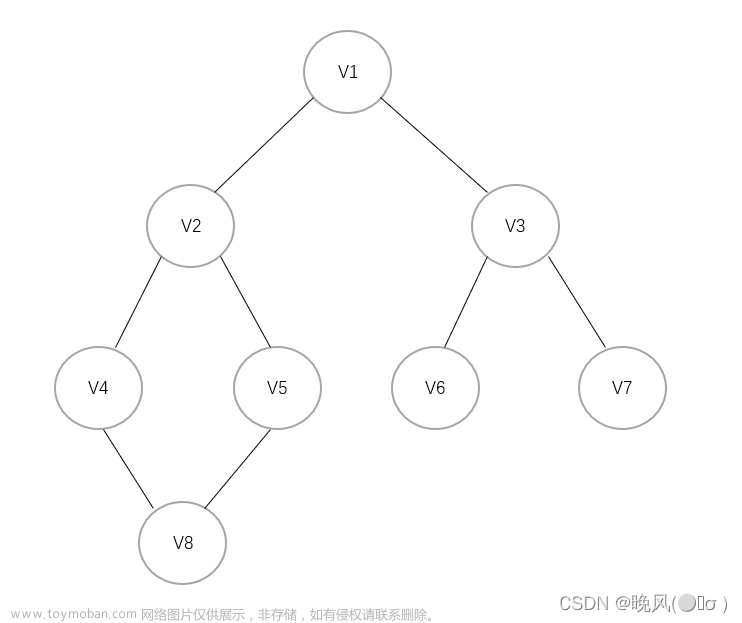
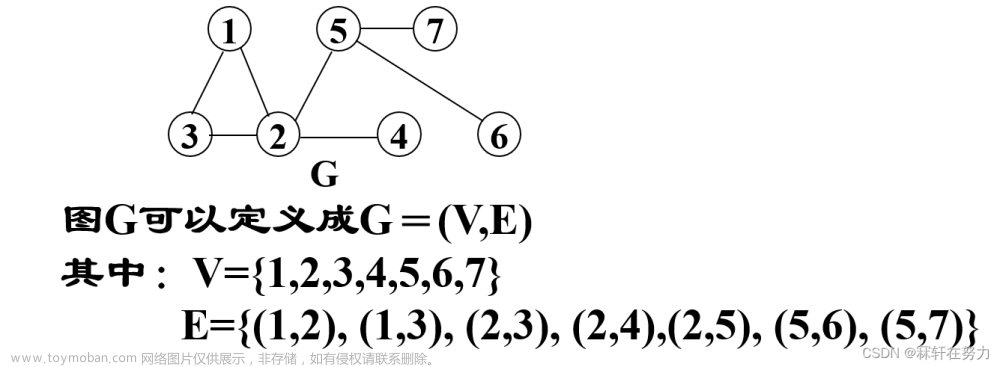
图是由顶点集合及顶点间的关系组成的一种数据结构：G = (V， E)，具体的：

  • 顶点集合V = {x|x属于某个数据对象集}是有穷非空集合；
  • E = {(x,y)|x,y属于V}或者E = {|x,y属于V && Path(x, y)}是顶点间关系的有穷集合，也叫做边的集 合。

(x, y)表示 x 到 y 的一条双向路径，即(x, y)是无方向的；Path<x, y>表示从x到y的一条单向通路，即Path是有方向的。例如下图：

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

顶点和边：图中结点称为顶点，第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边， 图中的第k条边记作ek，ek = (vi，vj)或，<vi, vj>。例如下图：

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

有向图和无向图：

  • 在有向图中，顶点对是有序的，顶点对，y>称为顶点x到顶点y的一条边(弧)，和是两条不同的边；
  • 在无向图中，顶点对(x, y)是无序的，顶点对(x,y)称为顶点x和顶点y相关联的一条边，这条边没有特定方向，(x,  y)和(y，x)是同一条边；

例如下图：

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

完全图：

  • 在有n个顶点的无向图中，若有n * (n - 1) / 2条边，即任意两个顶点之间有且仅有一条边，则称此图为 无向完全图；
  • 在n个顶点的有向图中，若有n * (n-1)条边，即任意两个顶点之间有且仅有方向 相反的边，则称此图为有向完全图；

例如下图：

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

邻接顶点：

  • 在无向图中G中，若(u, v)是E(G)中的一条边，则称u和v互为邻接顶点，并称边(u,v)依附于顶点u和v；
  • 在有向图G中，若是E(G)中的一条边，则称顶点u邻接到v，顶点v邻接自顶点u，并称边与顶点u和顶点v相关联。

顶点的度：

顶点v的度是指与它相关联的边的条数（类似树的度），记作deg(v)。在有向图中，顶点的度等于该顶点的入度与 出度之和，其中顶点v的入度是以v为终点的有向边的条数，记作indev(v);顶点v的出度是以v为起始点的有向 边的条数，记作outdev(v)。因此：dev(v) = indev(v) + outdev(v)。注意：对于无向图，顶点的度等于该顶 点的入度和出度，即dev(v) = indev(v) = outdev(v)。

路径：在图G = (V， E)中，若从顶点vi出发有一组边使其可到达顶点vj，则称顶点vi到顶点vj的顶点序列为从 顶点vi到顶点vj的路径。

路径长度：

  • 对于不带权的图，一条路径的路径长度是指该路径上的边的条数；
  • 对于带权的图，一条路径的路 径长度是指该路径上各个边权值的总和。

例如下图：

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

简单路径与回路：若路径上各顶点v1，v2，v3，…，vm均不重复，则称这样的路径为简单路径。回路或环：路径上第一个顶点v1和最后一个顶点vm重合。

例如下图：

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

 子图：设图G = {V, E}和图G1 = {V1，E1}，若V1属于V且E1属于E，则称G1是G的子图

例如下图：

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

连通图：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图。

例如下图：

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

强连通图：在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj到 vi的路 径，则称此图是强连通图。

例如下图：

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

生成树：一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条 边。

二、图的存储结构

2.1、存储结构

在图的存储中，只需要保存：节点和边的关系即可～

2.1、邻接矩阵（考察重点）

邻接矩阵就是用矩阵（二维数组）来表示图的节点和边的关系，其中用 1 表示连通，0表示不连通.

如下无权值：

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

如下有权值：

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

2.1.1、代码实现

import java.util.Arrays;

public class GraphByMatrix {

    private char[] arrayV;//顶点数组
    private int[][] matrix;//邻接矩阵
    private boolean isDirect;//是否是有向图

    /**
     * @param size 代表当前顶点的个数
     * @param isDirect
     */
    public GraphByMatrix(int size, boolean isDirect) {
        this.arrayV = new char[size];
        matrix = new int[size][size];
        //这里约定：统一初始化为最大值
        for(int i = 0; i < size; i++) {
            Arrays.fill(matrix[i], Constant.MAX);
        }
        this.isDirect = isDirect;
    }

    /**
     * 初始化顶点
     * @param array
     */
    public void initArrayV(char[] array) {
        for(int i = 0; i < array.length; i++) {
            arrayV[i] = array[i];
        }
    }

    /**
     * 增加边
     * @param srcV 起点
     * @param destV 终点
     * @param weight 权值
     */
    public void addEdge(char srcV, char destV, int weight) {
        int srcIndex = getIndexOfV(srcV);
        int destIndex = getIndexOfV(destV);

        matrix[srcIndex][destIndex] = weight;
        //如果是无向图，那么相反的位置，也同样需要置为空
        if(!isDirect) {
            matrix[destIndex][srcIndex] = weight;
        }
    }

    /**
     * 获取顶点的下标
     * @param v
     * @return
     */
    private int getIndexOfV(char v) {
        for(int i = 0; i < arrayV.length; i++) {
            if(arrayV[i] == v)
            return i;
        }
        return -1;
    }

    /**
     * 获取顶点的度，有向图 = 入度 + 出度
     * @return
     */
    public int getDevofV(char v) {
        int count = 0;
        int srcIndex = getIndexOfV(v);
        for(int i = 0; i < arrayV.length; i++) {
            if(matrix[srcIndex][i] != Constant.MAX) {
                count++;
            }
        }

        //计算有向图的入度
        if(isDirect) {
            for(int i = 0; i < arrayV.length; i++) {
                if(matrix[i][srcIndex] != Constant.MAX) {
                    count++;
                }
            }
        }
        return count;
    }

    //打印数组
    public void printGraph() {
        for(int i = 0; i < matrix.length; i++) {
            for(int j = 0; j < matrix[i].length; j++) {
                if(matrix[i][j] == Constant.MAX) {
                    System.out.print("∞ ");
                } else {
                    System.out.print(matrix[i][j] + " ");
                }
            }
            System.out.println();
        }
    }

    //测试
    public static void main(String[] args) {
        GraphByMatrix graph = new GraphByMatrix(4, true);
        char[] array = {'A', 'B', 'C', 'D'};
        graph.initArrayV(array);

        graph.addEdge('A', 'B', 1);
        graph.addEdge('A', 'D', 1);
        graph.addEdge('B', 'A', 1);
        graph.addEdge('B', 'C', 1);
        graph.addEdge('C', 'B', 1);
        graph.addEdge('C', 'D', 1);
        graph.addEdge('D', 'A', 1);
        graph.addEdge('D', 'C', 1);

        graph.printGraph();
        //获取 A 的度
        System.out.println(graph.getDevofV('A'));
    }

}

 文章来源地址https://www.toymoban.com/news/detail-474490.html

2.2、邻接表

邻接表：使用数组表示顶点的集合，使用链表表示边的关系 。

2.3.1、无向邻接表存储

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

Ps：无向图中同一条边在邻接表中出现了两次。如果想知道顶点vi的度，只需要知道顶点vi边链表集 合中结点的数目即可。 

2.3.2、有向图邻接表存储

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

Ps：有向图中每条边在邻接表中只出现一次，与顶点vi对应的邻接表所含结点的个数，就是该顶点的 出度，也称出度表，要得到vi顶点的入度，必须检测其他所有顶点对应的边链表，看有多少边顶点的dst取值是i。

import java.util.ArrayList;

public class GraphByNode {

    static class Node {
        public int src;//起始位置
        public int dest;//目标位置
        public int weight;//权重
        public Node next;

        public Node(int src, int dest, int weight) {
            this.src = src;
            this.dest = dest;
            this.weight = weight;
        }
    }

    public char[] arrayV;
    public ArrayList<Node> edgList;//存储边
    public boolean isDirect;

    public GraphByNode(int size, boolean isDirect) {
        this.arrayV = new char[size];
        edgList = new ArrayList<>(size);
        for(int i = 0; i < size; i++) {
            edgList.add(null);
        }
        this.isDirect = isDirect;
    }

    /**
     * 初始化顶点
     * @param array
     */
    public void initArrayV(char[] array) {
        for(int i = 0; i < array.length; i++) {
            arrayV[i] = array[i];
        }
    }

    /**
     * 增加边
     * @param srcV 起点
     * @param destV 终点
     * @param weight 权值
     */
    public void addEdge(char srcV, char destV, int weight) {
        int srcIndex = getIndexOfV(srcV);
        int destIndex = getIndexOfV(destV);
        addEdgeChild(srcIndex, destIndex, weight);

        //无向图需要添加两条边
        if(!isDirect) {
            addEdgeChild(destIndex, srcIndex, weight);
        }
    }

    private void addEdgeChild(int srcIndex, int destIndex, int weight) {
        //这里拿到的是头结点
        Node cur = edgList.get(srcIndex);
        while(cur != null) {
            if(cur.dest == destIndex) {
                return;
            }
            cur = cur.next;
        }
        //之前没有存储过这条边
        Node node = new Node(srcIndex, destIndex, weight);
        node.next = edgList.get(srcIndex);
        edgList.set(srcIndex, node);
    }

    /**
     * 获取顶点的下标
     * @param v
     * @return
     */
    private int getIndexOfV(char v) {
        for(int i = 0; i < arrayV.length; i++) {
            if(arrayV[i] == v)
                return i;
        }
        return -1;
    }

    //获取顶点的度
    public int getDevOfv(char v) {
        int count = 0;
        int srcIndex = getIndexOfV(v);
        Node cur = edgList.get(srcIndex);
        while(cur != null) {
            count++;
            cur = cur.next;
        }

        //有向图
        if(isDirect) {
            int destIndex = srcIndex;
            for(int i = 0; i < arrayV.length; i++) {
                if(i == destIndex) {
                    continue;
                } else {
                    Node pCur = edgList.get(i);
                    while(pCur != null) {
                        if(pCur.dest == destIndex) {
                            count++;
                        }
                        pCur = pCur.next;
                    }
                }
            }
        }
        return count;
    }


    public void printGraph() {
        for(int i = 0; i < arrayV.length; i++) {
            System.out.print(arrayV[i] + "->");
            Node cur = edgList.get(i);
            while(cur != null) {
                System.out.print(arrayV[cur.dest] + " ->");
                cur = cur.next;
            }
            System.out.println();
        }
    }

    //测试
    public static void main(String[] args) {
        GraphByNode graph = new GraphByNode(4, true);
        char[] array = {'A', 'B', 'C', 'D'};
        graph.initArrayV(array);

        graph.addEdge('A', 'B', 1);
        graph.addEdge('A', 'D', 1);
        graph.addEdge('B', 'A', 1);
        graph.addEdge('B', 'C', 1);
        graph.addEdge('C', 'B', 1);
        graph.addEdge('C', 'D', 1);
        graph.addEdge('D', 'A', 1);
        graph.addEdge('D', 'C', 1);
        System.out.println("getDevOfV:" + graph.getDevOfv('A'));
        graph.printGraph();
    }

}

3.1、图的广度优先遍历（层序遍历）

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

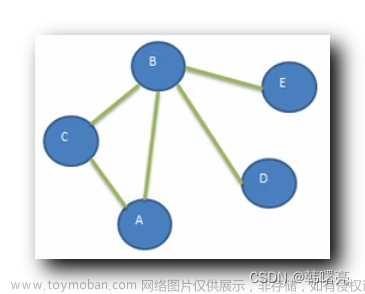
 类似于二叉树的层序遍历，也需要使用队列，首先将第一个元素（假设如上图中的B）放入队列，同时使用一个 boolean 类型数组标记这个元素已被放入（这样做是为了防止一个元素被多次放入），接着出队（将 B 弹出），将出队的元素的连通的结点（A，C结点）经检验不重复后（boolean 类型数组检验是否之前被放入过），再次放入队列，依次往复即可~


import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;

public class GraphByMatrix {

    private char[] arrayV;//顶点数组
    private int[][] matrix;//邻接矩阵
    private boolean isDirect;//是否是有向图

    /**
     * @param size 代表当前顶点的个数
     * @param isDirect
     */
    public GraphByMatrix(int size, boolean isDirect) {
        this.arrayV = new char[size];
        matrix = new int[size][size];
        //这里约定：统一初始化为最大值
        for(int i = 0; i < size; i++) {
            Arrays.fill(matrix[i], Constant.MAX);
        }
        this.isDirect = isDirect;
    }

    /**
     * 初始化顶点
     * @param array
     */
    public void initArrayV(char[] array) {
        for(int i = 0; i < array.length; i++) {
            arrayV[i] = array[i];
        }
    }

    /**
     * 增加边
     * @param srcV 起点
     * @param destV 终点
     * @param weight 权值
     */
    public void addEdge(char srcV, char destV, int weight) {
        int srcIndex = getIndexOfV(srcV);
        int destIndex = getIndexOfV(destV);

        matrix[srcIndex][destIndex] = weight;
        //如果是无向图，那么相反的位置，也同样需要置为空
        if(!isDirect) {
            matrix[destIndex][srcIndex] = weight;
        }
    }

    /**
     * 获取顶点的下标
     * @param v
     * @return
     */
    private int getIndexOfV(char v) {
        for(int i = 0; i < arrayV.length; i++) {
            if(arrayV[i] == v)
            return i;
        }
        return -1;
    }

    /**
     * 获取顶点的度，有向图 = 入度 + 出度
     * @return
     */
    public int getDevofV(char v) {
        int count = 0;
        int srcIndex = getIndexOfV(v);
        for(int i = 0; i < arrayV.length; i++) {
            if(matrix[srcIndex][i] != Constant.MAX) {
                count++;
            }
        }

        //计算有向图的入度
        if(isDirect) {
            for(int i = 0; i < arrayV.length; i++) {
                if(matrix[i][srcIndex] != Constant.MAX) {
                    count++;
                }
            }
        }
        return count;
    }

    //打印数组
    public void printGraph() {
        for(int i = 0; i < matrix.length; i++) {
            for(int j = 0; j < matrix[i].length; j++) {
                if(matrix[i][j] == Constant.MAX) {
                    System.out.print("∞ ");
                } else {
                    System.out.print(matrix[i][j] + " ");
                }
            }
            System.out.println();
        }
    }


    //广度优先遍历
    public void bfs(char v) {
        //数组用来标记顶点是否被使用过
        boolean[] visited = new boolean[arrayV.length];

        //定义一个队列，来辅助完成 bfs
        Queue<Integer> queue = new LinkedList<>();
        int srcIndex = getIndexOfV(v);
        queue.offer(srcIndex);
        while(!queue.isEmpty()) {
            int top = queue.poll();
            System.out.print(arrayV[top] + "->");
            visited[top] = true;//每次弹出一个元素就置为 true
            for(int i = 0; i < arrayV.length; i++) {
                if(matrix[top][i] != Constant.MAX && !visited[i]) {
                    queue.offer(i);
                    visited[i] = true;//每次入队就置为true
                }
            }
        }
    }

    //测试
    public static void main(String[] args) {
        GraphByMatrix graph = new GraphByMatrix(4, false);
        char[] array = {'A', 'B', 'C', 'D'};
        graph.initArrayV(array);

        graph.addEdge('A', 'B', 1);
        graph.addEdge('A', 'D', 1);
        graph.addEdge('B', 'A', 1);
        graph.addEdge('B', 'C', 1);
        graph.addEdge('C', 'B', 1);
        graph.addEdge('C', 'D', 1);
        graph.addEdge('D', 'A', 1);
        graph.addEdge('D', 'C', 1);

        graph.bfs('B');
    }

}

3.2、图的深度优先遍历

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

 

类似于二叉树的前序遍历，通过邻接矩阵进行优先遍历，例如起始位置为上图中的 B，那么上图中右边的邻接矩阵从竖列 B 元素开始向右，找到第一个不为 0 的，也就是通向 A 元素，那么接着再从竖列 A 元素开始向右，找到第一个不为 0 的，这里是 B 元素，但由于之前通向过 B 元素所以继续向右找不为 0 的，于此类推，最后得出 dfs 结果，如下代码

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;

public class GraphByMatrix {

    private char[] arrayV;//顶点数组
    private int[][] matrix;//邻接矩阵
    private boolean isDirect;//是否是有向图

    /**
     * @param size 代表当前顶点的个数
     * @param isDirect
     */
    public GraphByMatrix(int size, boolean isDirect) {
        this.arrayV = new char[size];
        matrix = new int[size][size];
        //这里约定：统一初始化为最大值
        for(int i = 0; i < size; i++) {
            Arrays.fill(matrix[i], Constant.MAX);
        }
        this.isDirect = isDirect;
    }

    /**
     * 初始化顶点
     * @param array
     */
    public void initArrayV(char[] array) {
        for(int i = 0; i < array.length; i++) {
            arrayV[i] = array[i];
        }
    }

    /**
     * 增加边
     * @param srcV 起点
     * @param destV 终点
     * @param weight 权值
     */
    public void addEdge(char srcV, char destV, int weight) {
        int srcIndex = getIndexOfV(srcV);
        int destIndex = getIndexOfV(destV);

        matrix[srcIndex][destIndex] = weight;
        //如果是无向图，那么相反的位置，也同样需要置为空
        if(!isDirect) {
            matrix[destIndex][srcIndex] = weight;
        }
    }

    /**
     * 获取顶点的下标
     * @param v
     * @return
     */
    private int getIndexOfV(char v) {
        for(int i = 0; i < arrayV.length; i++) {
            if(arrayV[i] == v)
            return i;
        }
        return -1;
    }

    /**
     * 获取顶点的度，有向图 = 入度 + 出度
     * @return
     */
    public int getDevofV(char v) {
        int count = 0;
        int srcIndex = getIndexOfV(v);
        for(int i = 0; i < arrayV.length; i++) {
            if(matrix[srcIndex][i] != Constant.MAX) {
                count++;
            }
        }

        //计算有向图的入度
        if(isDirect) {
            for(int i = 0; i < arrayV.length; i++) {
                if(matrix[i][srcIndex] != Constant.MAX) {
                    count++;
                }
            }
        }
        return count;
    }

    //打印数组
    public void printGraph() {
        for(int i = 0; i < matrix.length; i++) {
            for(int j = 0; j < matrix[i].length; j++) {
                if(matrix[i][j] == Constant.MAX) {
                    System.out.print("∞ ");
                } else {
                    System.out.print(matrix[i][j] + " ");
                }
            }
            System.out.println();
        }
    }


    //广度优先遍历
    public void bfs(char v) {
        //数组用来标记顶点是否被使用过
        boolean[] visited = new boolean[arrayV.length];

        //定义一个队列，来辅助完成 bfs
        Queue<Integer> queue = new LinkedList<>();
        int srcIndex = getIndexOfV(v);
        queue.offer(srcIndex);
        while(!queue.isEmpty()) {
            int top = queue.poll();
            System.out.print(arrayV[top] + "->");
            visited[top] = true;//每次弹出一个元素就置为 true
            for(int i = 0; i < arrayV.length; i++) {
                if(matrix[top][i] != Constant.MAX && !visited[i]) {
                    queue.offer(i);
                    visited[i] = true;//每次入队就置为true
                }
            }
        }
    }

    // 深度优先遍历
    public void dfs(char v) {
        //数组用来标记顶点是否被使用过
        boolean[] visited = new boolean[arrayV.length];
        int srcIndex = getIndexOfV(v);
        dfsChild(srcIndex, visited);
    }

    private void dfsChild(int srcIndex, boolean[] visited) {
        System.out.print(arrayV[srcIndex] + "->");
        visited[srcIndex] = true;
        for(int i = 0; i < arrayV.length; i++) {
            if(matrix[srcIndex][i] != Constant.MAX && !visited[i]) {
                dfsChild(i, visited);
            }
        }
    }

    //测试
    public static void main(String[] args) {
        GraphByMatrix graph = new GraphByMatrix(4, false);
        char[] array = {'A', 'B', 'C', 'D'};
        graph.initArrayV(array);

        graph.addEdge('A', 'B', 1);
        graph.addEdge('A', 'D', 1);
        graph.addEdge('B', 'A', 1);
        graph.addEdge('B', 'C', 1);
        graph.addEdge('C', 'B', 1);
        graph.addEdge('C', 'D', 1);
        graph.addEdge('D', 'A', 1);
        graph.addEdge('D', 'C', 1);

//        graph.bfs('B');
        graph.dfs('B');
    }
}

【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解

 

到了这里，关于【图】概念、存储结构、广度优先遍历遍历、深度优先遍历 - 详解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包