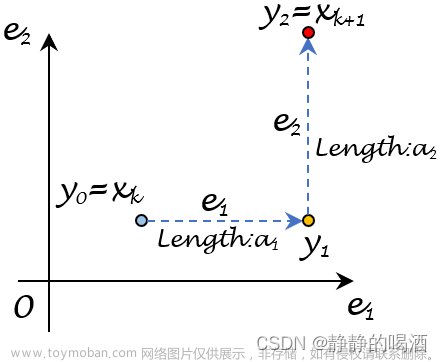
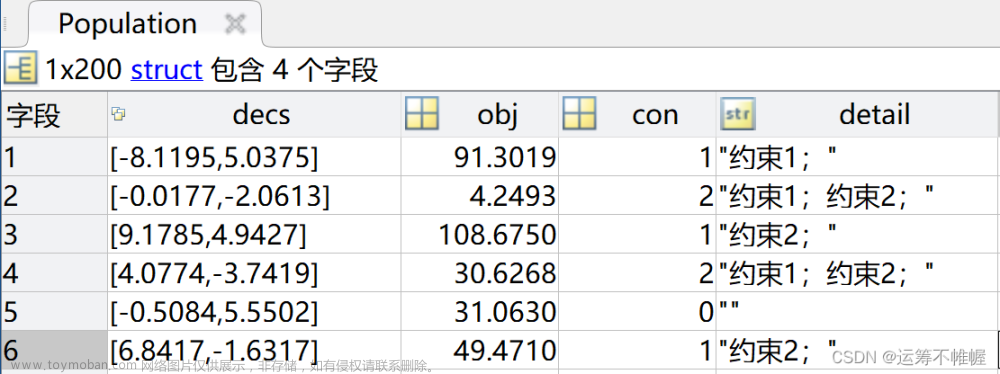
带约束的优化问题可被定义为:
在python中,可以使用scipy的optimize包进行求解,具体求解函数为linprog,下面举例说明求解方法:
假设问题被定义为:
首先,求解最大值问题,我们可以通过取负转换为求解最小值问题,包括不等式约束也是如此,那么该问题的python求解代码如下:
import numpy as np
from scipy.optimize import linprog
fun = np.array([-29.0, -45.0, 0.0, 0.0])
A_ub = np.array([[1.0, -1.0, -3.0, 0.0],
[-2.0, 3.0, 7.0, -3.0]])
b_ub = np.array([5.0, -10.0])
A_eq = np.array([[2.0, 8.0, 1.0, 0.0],
[4.0, 4.0, 0.0, 1.0]])
b_eq = np.array([60.0, 60.0])
x0_bounds = (0, None)
x1_bounds = (0, 5.0)
x2_bounds = (-np.inf, 0.5) # +/- np.inf can be used instead of None
x3_bounds = (-3.0, None)
bounds = [x0_bounds, x1_bounds, x2_bounds, x3_bounds]
result = linprog(fun, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds)
print(result.message)
上述代码会显示:
The problem is infeasible. (HiGHS Status 8: model_status is Infeasible; primal_status is At lower/fixed bound)
这说明问题无解,重新调整x1边界范围后,继续执行:
x1_bounds = (0, 6)
bounds = [x0_bounds, x1_bounds, x2_bounds, x3_bounds]
result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds)
print(result.message)
print(result.x)
print(result.fun)
终端显示:
Optimization terminated successfully.
[ 9.41025641 5.17948718 -0.25641026 1.64102564]
-505.97435889013434
这说明问题求解成功,当 x 1 = 9.41025641 , x 2 = 5.17948718 , x 3 = − 0.25641026 , x 4 = 1.64102564 x_1=9.41025641,x_2=5.17948718,x_3=-0.25641026,x_4=1.64102564 x1=9.41025641,x2=5.17948718,x3=−0.25641026,x4=1.64102564 目标函数取最大值,最大值为 505.97435889013434 505.97435889013434 505.97435889013434.
注意将最大值优化问题转换为最小值优化问题时,结果要再取反!文章来源:https://www.toymoban.com/news/detail-474870.html
参考文献:文章来源地址https://www.toymoban.com/news/detail-474870.html
- https://docs.scipy.org/doc/scipy/tutorial/optimize.html#linear-programming-linprog
到了这里,关于python求解带约束的优化问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!