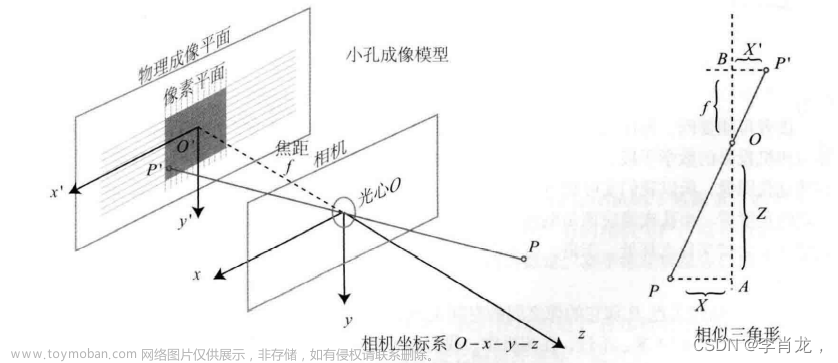
当机器人旋转轴上的夹爪中心不在旋转轴中心时，如何让旋转轴围绕夹爪中心旋转，这就是工具坐标系，怎末实现呢？机器人都是建立工具坐标系实现，这是什么原理？我们来探索一下：
世界上的有些特例让人拍案惊奇：
假定旋转中心o，到夹爪中心a，距离为2，也就是旋转半径为2，一半情况我们是让a围绕o旋转的，如何做到o围绕a旋转？
我们让a围绕o旋转60度，a到达b点，把b拖到a，o在什么地方？
因为是等边三角形，所以b在y方向移动，x方向移动1，就到达了a，也即o移动了，1到达了o"
那么，a围绕o”继续旋转60，到达c点，我们再把c点拖回到a，出现了什么情况？
c点和最初的o点重合了，由等边三角形可知，c拖回到a，o"到达o^,若定义o为（0，0），
a（-2，0）；
则o“为（-1，），o^为（-3，）
那么a再围绕o^旋转60度，a到达o”，a由o“再拖回到a，o到达（-4，0）
以上全为逆时针旋转（你也可以试试顺时针），可以看到a点没动（-2，0），旋转中心到达的四个点正好在以（-2，0）为中心，半径为2的圆上。
所以我们只要能算出旋转中心走过的坐标，就能让旋转中心围绕夹爪中心旋转。
这就是工具坐标系。（以前看到机器人再用，感到很神奇）
有时候，突然会想到卫星总想沿着切线方向脱离地球的引力，但就是这个力把它又拉回来了，这一刻叫做微观效应，实际和我们上面60度特例旋转是一样的，当我们由这种特例进入一种微观效应，或许，我们每一个人都会发现微积分。文章来源：https://www.toymoban.com/news/detail-474883.html
文章来源地址https://www.toymoban.com/news/detail-474883.html
到了这里，关于有趣的工具坐标系的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
