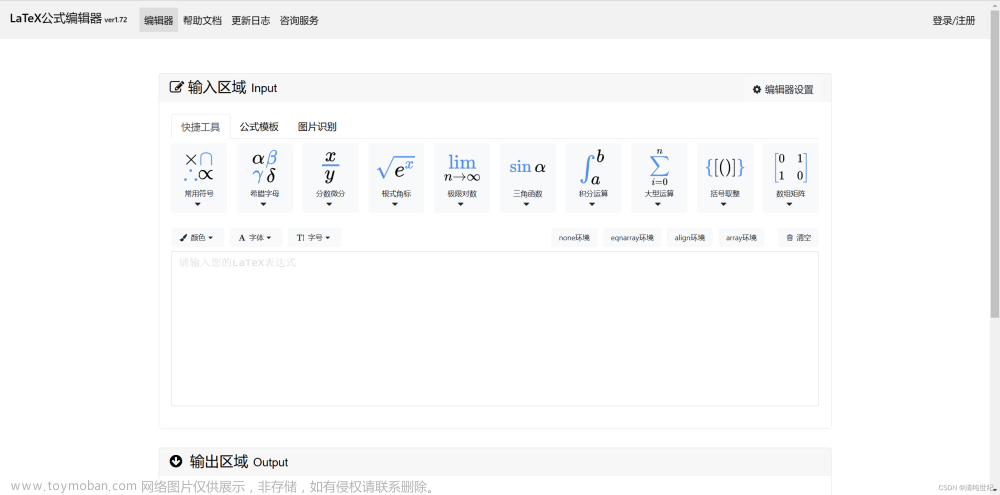
Latex常用数学编辑

Latex常用数学字母、公式

一、Latex常用希腊字母

二、Markdown使用Latex数学公式。

• 底下大括号：

  底下大括号代码：\underbrace{ a+b+\cdots+z }_{26}
  底下大括号结果：$\underset{26}{a+b+\cdots +z}$

• 矩阵行列式

  矩阵行列式代码：X=\left|
  \begin{matrix}
  x_{11} & x_{12} & \cdots & x_{1d}\
  x_{21} & x_{22} & \cdots & x_{2d}\
  \vdots & \vdots & \ddots & \vdots \
  x_{11} & x_{12} & \cdots & x_{1d}\
  \end{matrix}
  \right|
  矩阵行列式结果： X = ∣ x 11 x 12 ⋯ x 1 d x 21 x 22 ⋯ x 2 d ⋮ ⋮ ⋱ ⋮ x 11 x 12 ⋯ x 1 d ∣ X=\left| \begin{matrix} x_{11} & x_{12} & \cdots & x_{1d}\\ x_{21} & x_{22} & \cdots & x_{2d}\\ \vdots & \vdots & \ddots & \vdots \\ x_{11} & x_{12} & \cdots & x_{1d}\\ \end{matrix} \right| X= ​x11​x21​⋮x11​​x12​x22​⋮x12​​⋯⋯⋱⋯​x1d​x2d​⋮x1d​​ ​

• 分段函数

  分段函数代码：f(n)= \ begin{cases} n/2, & \ text{if n is even}\ 3n+1,& \ text{if n is odd} \ end{cases}——其中&后面是对齐。
  $f(n)=\{\begin{array}{ll}n/2,& \text{if n is even}\\ 3n+1,& \text{if n is odd}\end{array}$

• 积分
  积分代码：\lim{a+b}，\lim_{n\rightarrow+\infty}
  积分结果：$\lim a+b$${\lim }_{n\to +\infty }$

• 累加

  累加代码：\sum{a}，\sum_{n=1}^{100}{a_n}
  累加结果：$\sum a$，${\sum }_{n=1}^{100}{a}_n$

• 累乘

  累乘代码：\prod{x}，\prod_{n=1}^{99}{x_n}
  累乘结果：$\prod x$，${\prod }_{n=1}^{99}{x}_n$

• 微积分运算符

  y′x：\prime、∫：\int、∬ ：\iint、∭ ：\iiint、⨌：\iiiint、

  ∮ ：\oint、lim ：\lim 、∞ ：\infty 、∇：\nabla

• 逻辑运算符

  ∵ \because 、∴ \therefore 、∀ \forall 、∃ \exists 、 ≠\not= 、≯ \not> 、 ⊄：\not\subset

• 线性模型

线性代码：h(\theta) = \sum\limits_{j=0} ^n \theta_j x_j
线性结果：$h(\theta )=\sum _{j=0}^n{\theta }_j{x}_j$

• 方程组
  方程组代码： \ left \ {
  \ begin{array}{c}
  a_1x+b_1y+c_1z=d_1 \
  a_2x+b_2y+c_2z=d_2 \
  a_3x+b_3y+c_3z=d_3
  \ end{array}
  \ right.
  $$方程组结果：\{\begin{array}{c}{a}_{1}x+b_{1}y+c_{1}z=d_1\\ a_{2}x+b_{2}y+c_{2}z=d_2\\ a_{3}x+b_{3}y+c_{3}z=d_3\end{array}$$

• 矩阵行列式
  矩阵行列式代码：X=\ left(
  \ begin{matrix}
  x_{11} & x_{12} & \ cdots & x_{1d}\
  x_{21} & x_{22} & \ cdots & x_{2d}\
  \ vdots & \ vdots & \ ddots & \ vdots\
  x_{m1} & x_{m2} & \ cdots & x_{md}\
  \ end{matrix}
  \ right)
  =\ left(
  \ begin{matrix}
  x_1^T \
  x_2^T \
  \ vdots\
  x_m^T \
  \ end{matrix}
  \ right)

• 矩阵行列式结果： X = ( x 11 x 12 ⋯ x 1 d x 21 x 22 ⋯ x 2 d ⋮ ⋮ ⋱ ⋮ x m 1 x m 2 ⋯ x m d ) = ( x 1 T x 2 T ⋮ x m T ) 矩阵行列式结果： X=\left( \begin{matrix} x_{11} & x_{12} & \cdots & x_{1d}\\ x_{21} & x_{22} & \cdots & x_{2d}\\ \vdots & \vdots & \ddots & \vdots\\ x_{m1} & x_{m2} & \cdots & x_{md}\\ \end{matrix} \right) =\left( \begin{matrix} x_1^T \\ x_2^T \\ \vdots\\ x_m^T \\ \end{matrix} \right) 矩阵行列式结果：X= ​x11​x21​⋮xm1​​x12​x22​⋮xm2​​⋯⋯⋱⋯​x1d​x2d​⋮xmd​​ ​= ​x1T​x2T​⋮xmT​​ ​

• 多行公式对齐
  多行公式对齐代码：\ begin{aligned}
  \ cos2x &= \ cos ^ 2x - \ sin ^ 2x \
  &= 2\ cos^2x-1
  \ end{aligned}
  $多行公式对齐结果：\begin{array}{rl}\cos 2x& ={\cos }^{2}x-{\sin }^{2}x\\ & =2{\cos }^{2}x-1\end{array}$

• 并集正上标、正下标
  并集正上标、正下标代码：
  \bigcup \limits ^n_{m=1}E_m( x,y)=0，加\limits即可。
  $并集正上标、正下标结果：\bigcup _{m=1}^n{E}_m(x,y)=0$
  公式正下方代码：
  \hat{q} = \underset{q} \arg \min{q}
  公式正下方效果：$\hat{q}=\underset{q}{\mathrm{argmin}}q$

• 公式大括号
  公式大括号代码：
  \begin{matrix} \left{ \frac{ \sum\limits _ { n = 0 } ^ { N - 1 } s ^ { 2 } ( n ) } { \sum\limits _ { n = 0 } ^ { N - 1 } [ y ( n ) - s ( n ) ] ^ { 2 } } \right} \end{matrix}
  $公式大括号结果：SNR=\begin{array}{c}\left\{\frac{\sum _{n=0}^{N-1}{s}^2(n)}{\sum _{n=0}^{N-1}[y(n)-s(n){]}^2}\right\}\end{array}$文章来源地址https://www.toymoban.com/news/detail-475241.html

到了这里，关于Latex常用数学编辑的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！