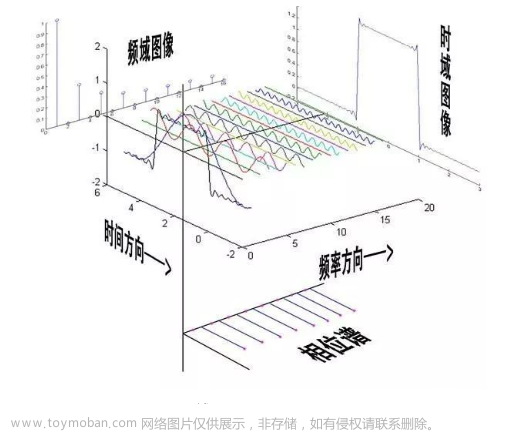
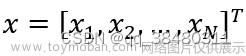opencv4 傅里叶变换-Toy模板网

这篇具有很好参考价值的文章主要介绍了opencv4 傅里叶变换。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

傅里叶变换

① 高频：变化剧烈的灰度分量，例如边界礁石。

② 低频：变化缓慢的灰度分量，例如一片大海。

③ 高通滤波器：只保留高频，会使得图像细节增强。高频边界锐化了，增强了，细节更明显了。

④ 低通滤波器：只保留低频，会使得图像模糊。低频信息保留下来了，高频信息没了，图像边界会变得模糊了。

① opencv 中主要就是 cv2.dft() 执行傅里叶变换到频域中和 cv2.idft() 执行逆傅里叶变换，输入图像需要先转换成 np.float32 格式。

② 得到的结果中频率为 0 的部分会在左上角，通常要转换到中心位置，可以通过 shift 变换来实现。

③ cv2.dft() 返回的结果是双通道的 ( 实部，虚部 )，通常还需要转换成图像格式才能展示(0,255)像素值。

ffshit

numpy.fft.fftshift() 函数是用来将一维或多维的数组进行循环移位（cyclic shift）操作，从而使得数据集的原点（中心点）从数组的开始位置移动到中间位置，便于进行傅里叶变换等操作。

具体来说，对于一维的实数或复数序列，numpy.fft.fftshift() 函数将其进行循环移位操作，将左半边的数据移到了右边，将右半边的数据移到了左边。而对于多维的数组，numpy.fft.fftshift() 函数则将其进行多维循环移位操作，保证每个维度上的数据都被移动到了中心位置。

举个例子，假设有一个长度为 N 的一维实数序列 x，其中 N 是偶数。那么按照 numpy.fft.fftshift() 的规则，可以将序列 x 划分为两部分：左半部分包括 x[N/2], x[N/2+1], …, x[N-1]；右半部分包括 x[0], x[1], …, x[N/2-1]。然后，在执行 numpy.fft.fftshift(x) 操作时，函数会将左半部分移到右边，将右半部分移到左边，得到新的序列 x’。此时，x’[0] = x[N/2], x’[1] = x[N/2+1], …, x’[N/2-1] = x[N-1]，x’[N/2] = x[0], x’[N/2+1] = x[1], …, x’[N-1] = x[N/2-1]。因此，numpy.fft.fftshift(x) 函数的作用就是将原始序列 x 在频域上进行循环移位操作，使得序列中心点移到了序列的开始位置，方便进行傅里叶变换等操作。

需要注意的是，numpy.fft.fftshift() 函数默认将原始序列的中心点移到了数组的开始位置，如果需要将中心点移到数组的结束位置，可以使用 numpy.fft.ifftshift() 函数进行逆向的移位操作。