1.3.1 树与二叉树-Toy模板网

这篇具有很好参考价值的文章主要介绍了1.3.1 树与二叉树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.3.1 树与二叉树

树是非线性结构。具体来说，树是层次结构。日常社会中，层次关系非常普遍，例如，家组谱系，组织机构关系等都是呈现一种层次结构。

1.3.1 树的基本概念

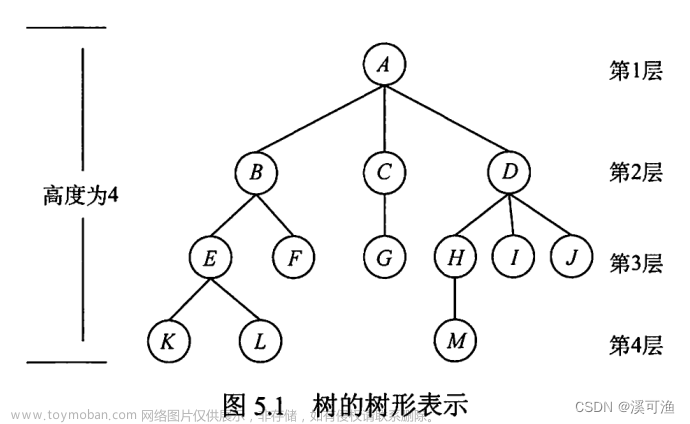
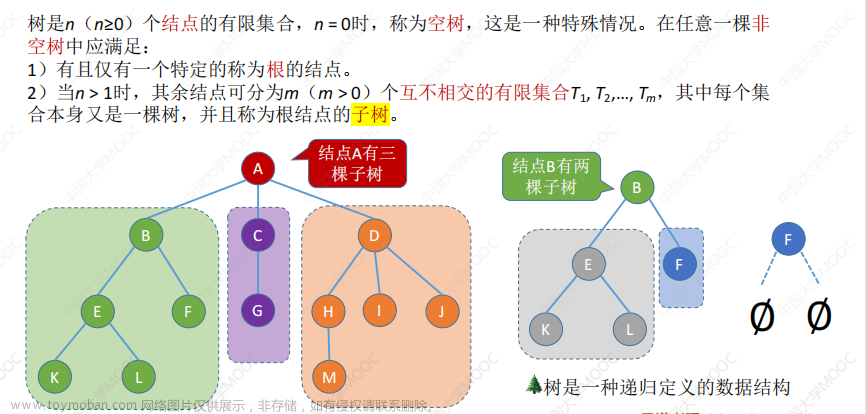
树T是n(n>0)个结点组成的有限集，其中有一个特定的结点R称为T的根，其余结点划分为不相交的子集T1，T2…,Tn。每个子集都是树，称为T的子树。每颗子树的根R1,R2,…Rm称为R的子结点或孩子，R称为R1,R2，‘’‘’‘’‘,Rm.的父亲结点或者双清，R1，R2,…,Rm互称为兄弟结点。树中每一个结点V的子结点个数M称为V的度，度为0的结点称为叶结点，度大于0的结点称为分支结点。

树的定义是一个递归的定义，这是树的固有特性决定的，树结构本身就是一个递归的结构。树的很多应用中都采用递归过程来实现。

1.3.2二叉树

二叉树是一种重要的树形结构，应用面广也是考试中经常出现的考点。

1.二叉树的应以及其主要特性

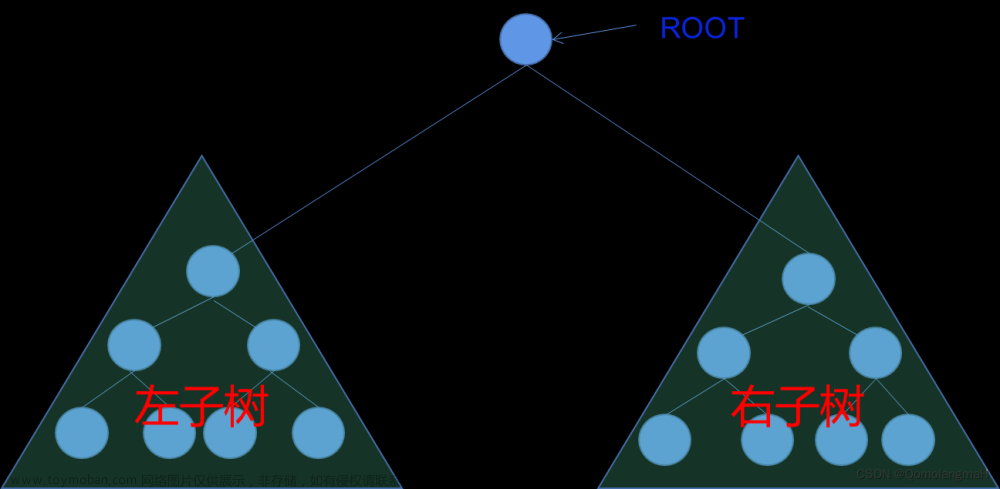
一颗二叉树T是n(n≥0)个结点组成的有限集，这个集合或为空，或由一个根结点R及两颗不相交的二叉树T1，T2组成T1，T2分别称为T的左子树和右子树，T1，T2的根R1，R2分别称为R的左子结点和右子结点。

二叉树中每个结点的度不大于2.二叉树中左子树与右子树的次序不能颠倒，但都可以存在或者为空，不同的存在状态可以组合称二叉树的5种基本形态，即两颗子树均为空或不为空，或者一颗为空，而另一颗不为空，还有空树。这5种形态。

2.二叉树的顺序存储结构和链式存储结构

1）二叉树的顺序存储结构

若V不是树根，则V的父结点保存在A[(i-1)/2]中

2）二叉树的链式存储结构

采用二叉链表保存二叉树T时，每个结点的结构为

lchild	data	rchild

其中data保存当前结点的值，lchild和rchild分别为指向当前左子结点和右子结点的指针。

typedef struct BinNode{     //二叉树结点类
    ElemType  data ;        //该结点的值
    struct BinNode * lchild; //指向左孩子结点的指针
    struct BinNode * rchild  //指向右孩子结点的指针
}

采用二叉链表保存二叉树T时，叶结点的两个指针域皆为NULL.。对于含n个结点的二叉树T，二叉树表中共有n-1个非空指针域，有n+1个空指针域。

静态链表保存在一堆数组中，数组单元包含三个域；lchild, data 和rchild。

在二叉链表中，查找某个结点的子结点非常方便，但不易查找父结点。为此，为每个结点增加一个指向父结点的指针域，结构定义为

lchild	data	parent	rchild

由此得到三叉链表。根结点的parent域为Null。

三叉链表也可以采用静态链表结构

静态链表保存在一堆数组中，数组单元包含四个域：

lchild	parent	data	rchild

其中data保存二叉树中结点的信息，lchild和rchild分别保存其左子几点及右子结点在数组下标，parent保存结点的父结点在数组中的下标。

3.二叉树的遍历

二叉树的遍历共有4种：先序遍历，中序遍历，后序遍历及层序遍历。

1）先序遍历

先序遍历又称为先根遍历或者前序遍历，过程如下；

如果二叉树T为空则返回，否则

访问根结点；
先序遍历T的左子树；
先序遍历T 的右子树。

2）中序遍历

中序遍历又称中根遍历，过程如下；

如果二叉树T为空则返回，否则
1. 中序遍历T的左子树；
2. 访问根结点；
3. 中序遍历T的右子树；
  
  3）后序遍历
  
  后序遍历又称为后根遍历，过程如下；
  
  如果二叉树T为空则返回，否则
  1. 后序遍历T的左子树；
  2. 后续遍历T的右子树；
  3. 访问根结点。
    
    给定二叉树的中序遍历序列，再加先序或后序遍历序列，可唯一确定二叉树，可以验证，仅给出一种遍历序列时，不能唯一确定二叉树。仅给出二叉树的先序遍历及后序遍历序列，也不能唯一确定二叉树。
    
    二叉树的先序遍历，中序遍历及后序遍历即可使用递归方法实现，也可适合非递归方式实现。
    
    4）层序遍历
    
    层序遍历的过程如下：
```
二叉树T的根结点入队列；
当队列不空时
{
出队列，并输出元素e;
若e有左子结点l,则l入队列；
若e有右子结点r,则r入队列；
}
```
  在层序遍历中，二叉树中的任意两个结点Ui 和Uj,若Ui先于Uj被遍历到，则Ui的子结点先于Uj的子结点被遍历到。
  
  4.线索二叉树的基本概念和构造
  
  二叉树的遍历结果得到结点的一个线性序列，在这个序列中，除第一个和最后一个结点外，每个结点都有一个且仅有一个前驱，有一个且仅有一个后继。遍历的过程就是不断寻找结点后继的过程。
  
  可以利用二叉链表中存在的空指针域指向结点的前驱和后继，得到线索树。对于树中的一个具体结点来说，不同的遍历序列中，它的前驱可能是不同的，后继也可能是不同的。因此，线索树又分为先序线索树，中序线索书及后序线索树。以中序线索树为例，线索树中结点的定义为
  
  lchild iTag data rTag rchild

iTag ={ 0， lchild域指向结点的左孩子结点

1， lchild域指向结点的中序遍历前驱}

rTag = { 0, rchld 域指向结点的右孩子结点。

rchild域指向结点的中序遍历后继}

在中序线索树种寻找结点v 的后序结点时，有以下集中情况；

（1）若V，rTag = =1 且 V，rchild! = NULL,则v,rchild指向的结点即为V的后续结点。

（2）若V，rTag = = 1 且 V，rvhild = = NuLL，则v为中序序列的最后一个结点，无后继结点。

（3）若V， rTag = = 0 且 V，rchild! = NuLL,则v的右子树中序遍历的第一个结点为V 的后继；

（4）若v,rTag = = 0 且 v,rchild = = NULL,无此种情况出现。

那么，情况（3）中，右子树中序遍历序列的第一个结点是哪个呢？从右子树的根开始沿 lchild指针向下，找到lchild == NuLL的结点即是。在建立线索树之前，这个空指针还没有指向它的前驱。若已经建立了线索树，则找到V,Ltag = = 1 的结点即是。

1.3.3树，森林

1.树的存储结构
1. 父结点表示法
  
  父结点表示法有静态实现及动态实现两种。
  
  静态实现父亲结点表示法时，使用一堆数组保存相关信息。数组的每个单元包括两个域，分别是数据域data及父结点域parent,data域保存结点的信息，parent保存该结点的父节点在数组下标。树根结点的父结点域中保存-1，这是树中唯一没有父结点的结点。多棵树可以同时保存在一个数组中。检查数组中parent域为-1的结点，可知数组保存的树的个数。
  
  动态实现父结点表示法时，树中结点的定义为
  
  data parent
  
  其中data保存树中结点信息，parent保存指向父结点的指针。
  
  根结点的parent域为NULL,这是树中唯一的一个空指针。
  
  2.孩子结点表示法
  
  树中每个结点的子结点个数差别个数差别可能很大，为了适应每个结点可以有不同数目的子结点的情况，可以使用链表保存子节点的情况。每个结点v1的所有子结点组成一个单链表L，这些链表的表头指针保存在一个数组中。
  
  3.左孩子右孩子表示法
  
  使用与二叉链表类似的一种结构，每个结点的结构为
  
  fchlid data nsibling
  
  其中，data域保存结点的信息，fchild域保存指向该结点第一个孩子的指针，nsibling域保存指向该结点下一个兄弟结点的指针。
  
  由于每一个结点都含有两个指针域，它很想是用来表示二叉树的二叉树链表结构，所以这种表示法又称为二叉树链表表示法。
  
  2.森林与二叉树的转换
  
  树的左孩子右兄弟表示法中，每个结点有两个指针，分别指向当前结点的左子结点及右兄弟结点。可以将这样的结构看作是二叉链表，一个二叉链表即可以解释为一棵树，又可以解释为一棵二叉树。由此在树与二叉树之间建立了关系。二叉树表成为他们相互转换的桥梁。
  
  若森林转换成二叉树的递归描述如下：
  
  如果F={T1,T2,‘’‘’‘’',Tn}是森林，则按如下规则将其转换为一颗二叉树B={root,LB,RB};
  - 若F为空，则B为空树
  - 若F非空，则B的根rooot为F中第一颗树T1的根;B的左子树 LB是从T1根据点的子树森林F1={T11，T12，、、、、T1n1}转换而成的二叉树；其右子树RB是从森林F={T2，T3，‘’‘’‘’‘，Tn}转换而成二叉树。
    
    3.树和森林的遍历
    
    树的遍历方式有两种，先序遍历和后续遍历。
    
    树的先序遍历过程；先访问根结点，再依次由左至右对每颗子树进行先序遍历。
    
    树的后续遍历过程；先依次由左至右对每颗子树进行后序遍历，再访问根结点。
    
    将树T转换为二叉树B，则树T的后序遍历序列与B的中序遍历序列相同。
    
    森林的遍历方式右两种：先序遍历和后序遍历。
    
    1）先序遍历
    
    先序遍历过程如下；
    
    如果森林为空则返回，否则
    - 访问森林中第一棵树的根结点
    - 先序遍历第一颗树根结点的子树森林
    - 先序遍历除去第一棵树之外剩余的树组成的森林。
      
      2)后序遍历
      
      后序遍历过程如下；
      
      如果森林为空则返回，否则
      - 后序遍历第一棵树根结点的子树森科；
      - 访问森林中第一棵树的根结点
      - 后序遍历除去第一棵树之外剩余的书组成的森林。
        
        1.3.4 树与二叉树的应用
        
        1.二叉排序树
        
        二叉排序树(BST)或者是一颗空树，或者是具有下列性质的二叉树；
        
        若它的左子树不为空，则左子树中所有结点的值均小于树根结点的值。
        
        若它的右子树不为空，则右子树中所有结点的值均大于等于数根结点的值。
        
        其左右子树也分别是二叉排序树。
        
        二叉排序树也称为二叉查找树，采用二叉链表结构存储。
        
        由于二叉排序树的有序性，在树中进行查找的效率较高。查找的对象称为查找目标，若找到称为查找成功；否则称为查找失败。
        
        二叉排序树各结点中保存的值称为关键字，有那些应用中，要求关键字具有唯一性。
        
        二叉排序树的每颗子树仍是二叉排序树。每个结点的左子结点的值均小于结点本身的值，其右子结点的值均大于等于结点本身的值。这个条件是其必要条件而非充分条件，换句话说，若一颗二叉树中每个结点左子结点的值小于结点的值，其右子结点的值大于等于结点的值，则树不一定是二叉排序树。
        
        二叉排序树T中的最小值位于其’‘左下角’，即从根开始沿指针lchild一直“”向下“，直到指针lchild为空的结点。同样，T中的最大值位于其”右下角“，即从根开始沿指针rchild一直”向下“，直到指针rchild为空的结点。
        
        对二叉排列树进行中序遍历，可得到一个升序序列。这是二叉排序树的特性之一。
        
        对于一般二叉树来说，仅直到树的先序序列或后序序列，不能唯一确定这棵二叉树。但是具体到二叉排序树。文章来源地址https://www.toymoban.com/news/detail-475340.html