斐波那契算法的理解-Toy模板网

这篇具有很好参考价值的文章主要介绍了斐波那契算法的理解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

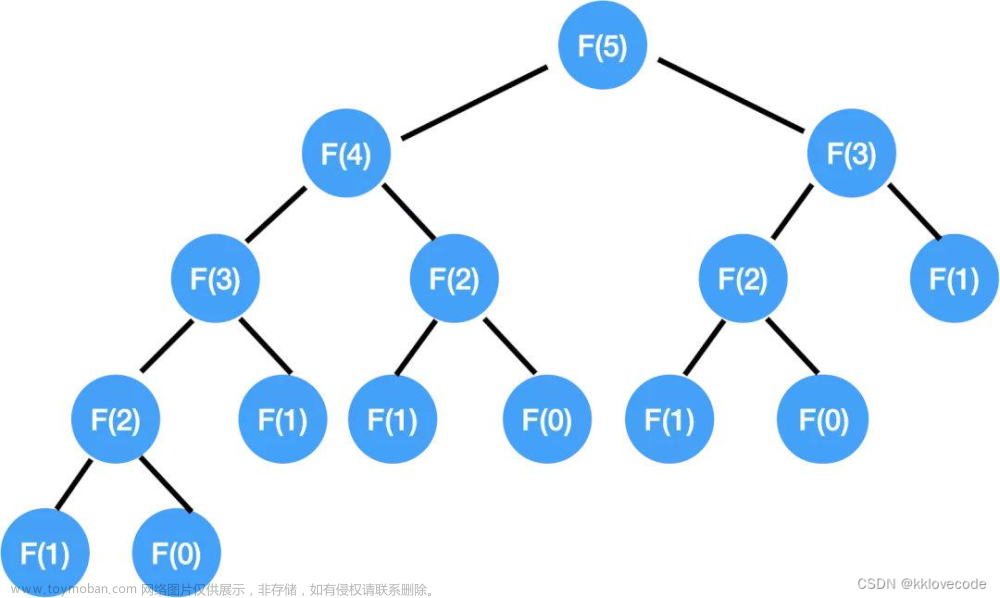
1.斐波那契数列 ：

数组：int[] F={1, 1, 2, 3, 5, 8, 13, 21, 34, 55 };

特点：

从第三个数开始，后边每一个数都是前两个数的和。F[k]=F[k-1]+F[k-2];

斐波那契算法的理解

如图所示：

①low、mid、high都是F数组的索引，F[k]-1表示长度。

②为了方便计算出mid，变形：F[k]-1 = (F[k-1]-1) + (F[k-2]-1) + 1;(多出来的1，可以当作mid)

③high=(F[k]-1)-1;

mid=low+F[k-1]-1;

2.需求：

现在有一个数组int[] arr={1,8,10,89,1000，1234}，长度n=6；

需要定义一个方法，从arr数组中找到数值为80(key=80)，

若有，则返回索引，若没有，就返回-1。

分析：

①黄金分割点：　

黄金比例又称黄金分割，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1:0.618或1.618:1。

结论：

只要顺序表的长度是F[k]-1，就可以分成两段：较大部分F[k-1]-1，和较小部分F[k-2]-1。

③黄金分割点，是按照长度来划分，与索引有密切关系。

一旦确定了数组arr的黄金分割点mid，之后就可以拿着我们要找的80与黄金分割点mid索引的元素值比较。再之后与二分查找类似。

④arr数组的长度n，是固定的值6，由于(F[k]-1)是不定的，最大值可以非常大，可看成无限大。

所以总是会存在：(F[k]-1)的值刚好大于或等于长度6。

arr数组的长度n确定了，那么(F[k]-1)的值也就确定了。

因此只要arr数组中元素个数n能达到此时的(F[k]-1)，就可以把arr数组分成两段，从而确定黄金分割点。

⑤新建一个数组brr，长度为(F[k]-1)。然后把arr这个数组中的数据全都拷贝到brr数组中，不足的部分先用0补充，最后把0换成arr的最后一个元素来补充(即arr[high])。

拿着key=80,与brr[mid]比较，

若key大，就把黄金分割点及右侧的部分都删除。

若key小,就把黄金分割点及左侧的部分都删除。

然后产生新的黄金分割点，再比较，直至两者相等，

若最终一直没找到，low>high就停止寻找。文章来源地址https://www.toymoban.com/news/detail-475443.html

到了这里，关于斐波那契算法的理解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

斐波那契算法的理解