期末三天赛高考我真的会谢,三天学完数据挖掘……真的很极限了的。
课本是那本绿色的Python数据分析与挖掘实战(第2版),作者张良均…
图片来自老师给的ppt,以下内容是我自己总结的,自己复习用,覆盖了老师给画的重点考点,八九不离十,期末考抱佛脚的可以看看。禁止转载哦。
再强调一下,只涵盖我们的考试重点,不是整本书的完整内容。
目录
一、数据质量分析
1-1数据分析常用的第三方库
1-2异常值分析
二、数据特征分析
2-1.常见数据特征分析方法
2-2基本统计特征函数
三、数据预处理
3-1数据清洗——缺失值处理
3-2数据变换——规范化
3-3数据规约——属性规约
3-4主要数据预处理函数
四、挖掘建模
4-1分类与预测
4-2聚类分析
4-3关联分析
4-4时序模式
文章来源地址https://www.toymoban.com/news/detail-475616.html
一、数据质量分析
1-1数据分析常用的第三方库
要知道它们各自的用处
| 扩展库 | 简介 |
|---|---|
| Numpy | 提供数组支持,以及相应的高效的处理函数 |
| Pandas | 强大、灵活的数据分析和探索工具 |
| Matplotlib | 强大的数据可视化工具、作图库 |
| Scipy | 提供矩阵支持,以及矩阵相关的数值计算模块 |
| StatsModels | 统计建模和计量经济学 |
| Scikit-Learn | 支持回归、分类、聚类等强大的机器学习库 |
1-2异常值分析
1.脏数据通常包括:
- 缺失值
- 异常值
- 不一致的值
- 重复数据及含有特殊符号的数据
2.异常值分析:又称离群点分析。主要方法有:简单统计量分析、3∂原则、箱形图分析。
3.箱形图分析:

二、数据特征分析
2-1.常见数据特征分析方法
生气了,这一大部分码了一个小时,一个不小心全没了,又要重新打一遍tmd
1.方法:
- 分布分析
- 对比分析
- 统计量分析
- 周期性分析
- 贡献度分析
- 相关性分析
2.分布分析:分布分析能揭示数据的分布特征和分布类型,便于发现某些特大或特小的可疑值。对于定量数据:欲了解数据的分布形式是对称的、还是非对称的,可做出频率分布表、绘制频率分布直方图等进行直观地分析。 对于定性数据:可用饼图和条形图直观地显示分布情况。
3.对比分析:指把两个相互联系的指标数据进行比较,从数量上展示和说明研究对象规模的大小,水平的高低,速度的快慢,以及各种关系是否协调。特别适用于指标间的横纵向比较、时间序列的比较分析。在对比分析中,选择合适的对比标准是十分关键的步骤。主要有两种方式:绝对数比较和相对数比较。
4.统计量分析:用统计指标对定量数据进行统计描述,常从集中趋势和离中趋势两个方面进行分析。
(1)集中趋势:一组数据向某一中心值靠拢的程度,度量主要有:均值、中位数、众数。
均值、中位数、众数怎么求的要会,小学生都会。注意偶数位的数求中位数的话就是取中间两个数和的一半。
(2)离中趋势:数据之间的差距和离散程度。度量主要有:极差、标准差、变异系数、四分位数间距(箱形图分析用到了)。
- 极差:极大值-极小值
- 标准差:

- 变异系数:

- 四分位数间距IQR:IQR的值越大,说明数据的变异程度越大,反之则越小。

5.相关性分析:分析连续变量之间线性的相关程度的强弱,并用适当的统计指标表示出来的过程。主要方法有:
- 直接绘制散点图

- 绘制散点图矩阵:如图所示,对角线是单个变量的分布,上下三角是变量两两之间的关系。

- 计算相关系数:主要掌握Pearson相关系数。


Pearson相关系数适用条件:
- 两个变量都是连续变量。
- 两个连续变量应当是成对的数据。
- 两个连续变量之间存在线性关系。通常做散点图检验该假设。
- 两个变量均没有明显的异常值。Pearson相关系数易受异常值影响。
- 两个变量符合双变量正态分布。
2-2基本统计特征函数
| 方法名 | 函数功能 | 所属库 |
|---|---|---|
| sum() | 求和 | Pandas |
| mean() | 求算术平均数 | |
| var() | 求方差 | |
| std() | 求标准差 | |
| corr() | 求Spearman(Pearson)相关系数矩阵 | |
| describe() | 给出样本的基本描述 |
三、数据预处理
3-1数据清洗——缺失值处理
1.缺失值处理方法有三类:删除记录、数据插补和不处理
2.数据插补——拉格朗日插值法
(1)思路:

(2)优缺点:
优点:插值公式结构紧凑,在理论分析中使用方便。
缺点:当插值节点增减时,插值多项式就会随之发生变化,每个插值基函数就需要重新计算;当多项式的n值取太高插值次数越高,会引起较大震荡,产生的插值结果就会越偏离原来函数的现象,即所谓的龙格现象。
3-2数据变换——规范化
1.规范化方法:最小-最大规范化、零-均值规范化、小数定标规范化
2.为什么要进行规范化;为了消除指标之间的量纲和大小不一的影响。
3.三种规范化方法的公式:(考代码)

文章来源:https://www.toymoban.com/news/detail-475616.html
3-3数据规约——属性规约
1.属性规约:通过合并或删除不相关属性来减少属性维数可将数据进行规约
2.属性规约常用方法:
合并属性;
删除不相关属性:逐步向前选择、逐步向后删除、决策树归纳;
数据降维:主成分分析(PCA)。
3.主成分分析(PCA):(知道步骤、代码实现)
(1)得到观测矩阵X
(2)将X标准化
(3)求相关系数矩阵R
(4)求R的特征方程的特征根
(5)确定主成分个数m
(6)计算m个相应的单位特征向量
(7)计算主成分
3-4主要数据预处理函数
| 函数名 | 函数功能 | 所属扩展库 |
| drop_duplicates | 去重 | Numpy、Pandas |
| isnull | 判断是否为空 | Pandas |
| notnull | 判断是否非空 | Pandas |
| dropna | 删除空值 | Pandas |
| fillna | 填补空值 | Pandas |
| PCA | 对指标变量矩阵进行主成分分析 | Scikit-learn |
四、挖掘建模
4-1分类与预测
1.分类:构造分类器或分类模型来预测离散属性。
预测:构造预测器预测连续属性。
2.分类的两步过程:
学习步:通过归纳分析训练样本集来建立分类模型得到分类规则。
分类步:先用已知的检验测试集评估分类规则的准确率,如果准确率可接受,则使用该模型对问未知类标号的待测样本集进行预测
预测模型的实现也有两步,同上,先得到模型,然后模型通过检验后再进行预测。
3.主要分类与预测算法
(1)回归分析:
| 回归模型 | 适用条件 | 算法描述 |
| 线性回归 | x与y是线性关系 | 用最小二乘法求解 |
| 非线性回归 | x与y是非线性关系 | 用非线性最小二乘法求解 |
| Logistic回归 | y一般有1-0两种取值 | 利用Logistics函数将因变量的取值范围控制在0和1之间,表示取值为1的概率 |
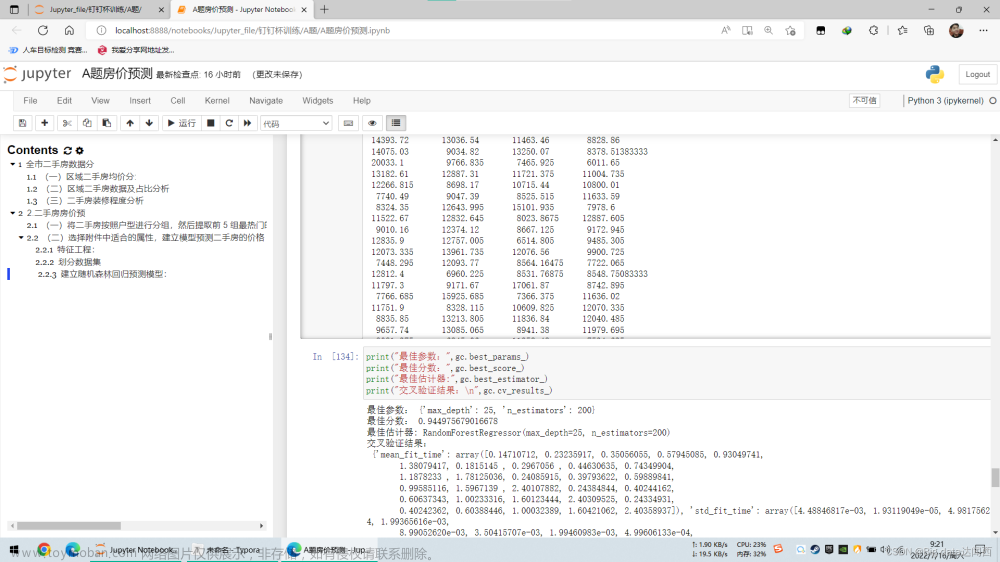
(2)决策树:ID3算法,例题:


 4.分类与预测算法评价:模型预测效果评价,通常用相对绝对误差、平均绝对误差、根均方差、相对平方根误差、Kappa系数、准确率、精确率、召回率、ROC曲线等评估指标来衡量。
4.分类与预测算法评价:模型预测效果评价,通常用相对绝对误差、平均绝对误差、根均方差、相对平方根误差、Kappa系数、准确率、精确率、召回率、ROC曲线等评估指标来衡量。
(1)混淆矩阵:描绘样本数据的实际结果与预测结果之间的关系。
如二分类混淆矩阵:
| 实际类\预测类 | C1 | - C1 |
|---|---|---|
| C1 | TP | FN |
| -C1 | FP | TN |
(2)Kappa统计:统计分析中Kappa系数可用来衡量两个变量一致性的指标。对于分类问题,所谓一致性就是模型预测结果和实际分类结果是否一致。
kappa系数的计算是基于混淆矩阵的,系数 k 为:

po 是每一类正确分类的样本数量之和除以总样本数,也就是总体分类精度,

看概念难懂,直接看例题吧:
这是一个三分类混淆矩阵:



(3)识别准确度Accuracy、精确度Precision、召回率Recall、F-度量、灵敏度、特异性:




例子:


5.评测分类器准确率常用技术:


4-2聚类分析
1.K-Means算法
(1)算法实现:直接看例子:

(2)优缺点:
优点:
- 算法实现快速、简单
- 对于处理大数据集,该算法是可伸缩的、有效的
- 当结果簇是密集的,它的效果较好
缺点:
- 只有当簇均值有定义的时候才能用
- 必须事先确定簇的个数
- 对初始值敏感,初始值不同可能产生不同结果
- 对“噪声”和孤立点数据敏感
2.算法评价:组内相似性越大,组间差异越大,聚类效果越好
评价方法:内部评价 + 外部评价
内部评价:无监督的方法,无需基准数据(Ground Truth),侧重类内聚集程度和类间
离散程度。
例如:轮廓系数(Silhouette Coefficient)、Calinski-Harabasz指数、邓恩指数等。
外部评价:有监督的方法,用一定的度量评判聚类结果与基准数据的符合程度。
例如: Purity评价法、RI评价法、F值评价法等。
3.Purity 评价法是一种简单的聚类评价方法。为了计算Purity,把每个簇中最多的类作为这个簇所代表的类,然后计算正确分类的聚类数占总数的比例。
eg:
4.RI评价法法是一种用排列组合原理来对聚类进行评价的手段,该方法将聚类看成是一系列的决策过程,RI就是计算“正确决策”的比率(即精确率,Accuracy),公式如下:

4-3关联分析
1.频繁模式:频繁出现在数据集中的模式(如项集)
项集:是项的集合。如{牛奶、麦片、糖果}是一个3项集。
项集的出现频率/频度是包含项集的事物计数,又称为绝对支持度或支持度计数。
2.关联规则分析:从大量数据中发现频繁模式,以挖掘数据或特征之间的关联或相关性。

3.关联规则的一般形式:
(1)项集A和B同时一起发生的概率称为关联规则的支持度:
Support(A -> B) = P(A ^ B)
(2)项集A发生的情况下,B也发生的概率称为关联规则的置信度:
Confidence ( A -> B) = P(B | A) = P(AB) / P(A)
4.最小支持度和最小置信度:
衡量支持度/置信度的最低门槛。
同时满足最小支持度和最小置信度的规则称为强规则。
满足最小支持度的项集是频繁项集,频繁k项集通常记作Lk。
5.支持度计数:项集A的支持度计数是指事物数据集中包含项集A的事物个数。
6.关联规则建模的一般步骤:
(1)找出所有频繁项集:频繁项集中每一项出现的次数都大于等于最小支持度计数。
(2)由频繁项集产生强关联规则:强关联规则必须满足最小支持度和最小置信度。
eg:对如下事务集,令最小支持度为0.5,最小置信度为0.5.
可以得到频繁项集为 {A,B,D,E,AD}(考虑到ABCDEF的各种组合,只有以上五个满足最小支持度)
强关联规则:(注意:由频繁项集产生强关联规则,上一步得到的频繁项集只有AD是两项的,所以只要考虑AD)
A->D 支持度0.6,置信度1
D->A 支持度0.6,置信度0.75
以上两组满足最小支持度和最小置信度,所以是强关联规则。
7.极大(最大)频繁项集:简单理解为该频繁项集不是其他频繁项集的子集。
8.Apriori算法:挖掘频繁项集的算法。
(1)重要先验性质:
频繁项集的所有非空子集也是频繁项集。如ABC是频繁项集,则它的子集AB、B等都是频繁项集,反之,如果AB不是频繁项集,则ABC不可能是频繁项集。
(2)过程一:找出所有频繁项集






eg1:

eg2:


4-4时序模式
1.时间序列分析的目的就是给定一个已被观测了的时间序列,预测该序列的未来值。
2.时间序列分类及使用的模型:
| 时 间 ------->平稳性检验 序 列 |
平稳序列 ------->随机性检验 | 白噪声 | 不用分析 |
| 平稳非白噪声 | AR | ||
| MA | |||
| ARMA | |||
| 非平稳序列 | ARIMA | ||
3.序列的预处理:随机性检验和平稳性检验。
(1)随机性检验:
- 检验是不是纯随机序列(白噪声序列)。白噪声序列是没有信息可以提取的序列。
- 对于平稳非白噪声序列,他的均值和方差都是常数。ARMA是最常用的平稳序列拟合模型。
- 对于非平稳序列,由于他的均值和方差不稳定。处理方法是先将其专为平稳序列,然后建立ARMA模型来研究。如果一个时间序列经差分运算后具有平稳性,称该序列为差分平稳序列,可以使用ARIMA。
(2)平稳性检验:
- 自协方差、自相关系数用来衡量一个事件在不同时间点之间的相关程度。
- 平稳时间序列的性质:有常数均值和方差,一个时刻之后的另一个时刻自协方差和自相关系数是相等的。
4.平稳性检验方法:
(1)图检验:时序图和自相关图。
- 时序图检验:根据平稳时间序列的均值和方差都为常数的性质,平稳序列的时序图显示该序列值始终在一个常数附近随机波动,而且波动的范围有界、无明显趋势及无周期特征。如果有明显的趋势性或者周期性,那它通常不是平稳序列。eg:


- 自相关图检验:

eg:

(2)构造检验统计量:单位根检验。
单位根检验是指检验序列中是否存在单位根,存在单位根的就是非平稳时间序列。
eg.

5.随机性检验方法:一般是构造检验统计量。如:Q统计量(大样本)、LB统计量(小样本)。
6.拖尾与截尾:
(1)截尾:指时间序列的自相关函数(ACF)或偏自相关函数(PACF)在某阶后均为0的性质。即:在大于某个常数k后函数值快速趋于0或在0附近随机波动。
(2)拖尾:指ACF或PACF并不在某阶后均为0的性质。即:始终有非0取值,不会在k大于某个常数后函数值就恒等于0或在0附近随机波动。
eg:判断是拖尾还是截尾
判断方法:截尾比拖尾趋于零的速度更快,而且截尾在后期不会再有明显的递增。(
拖尾~拖拉~所以趋于0比较慢)


7.AR、MA、ARMA模型
(1)AR

(2) MA

(3)ARMA



8.ARIMA模型


eg.
🌟本文原创,如果对你有帮助的话欢迎点赞收藏哇!
🎈逢考必过~~
到了这里,关于Python数据分析与挖掘实战期末考复习(抱佛脚啦)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!