目录
介绍Prim算法前的相关概念
一、Prim算法的思想
二.1、利用图形详细解释Prim算法的思想
Prim算法思想介绍
二.2利用图形又又解释Prim算法的思想
三、用图示结合代码中重要量进行说明
四、代码实现(用c语言)
介绍Prim算法前的相关概念
- 带权图:边赋以权值的图称为网或带权图,带权图的生成树也是带权的,生成树T各边的权值总和称为该树的权。
- 生成树和最小生成树的应用:要连通n个城市需要n-1条边线路。可以把边上的权值解释为线路的造价,则最小生成树表示使其造价最小的生成树。
- 连通图:在无向图中,若任意两个顶点vivi与vjvj都有路径相通,则称该无向图为连通图。
- 强连通图:在有向图中,若任意两个顶点vivi与vjvj都有路径相通,则称该有向图为强连通图。
- 连通网:在连通图中,若图的边具有一定的意义,每一条边都对应着一个数,称为权;权代表着连接连个顶点的代价,称这种连通图叫做连通网。
- 生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
- 最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树
-
Prim算法是一种产生最小生成树的算法。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克发现;并在1957年由美国计算机科学家罗伯特·普里姆独立发现;1959年,艾兹格·迪科斯彻再次发现了该算法。Prim算法从任意一个顶点开始,每次选择一个与当前顶点集最近的一个顶点,并将两顶点之间的边加入到树中。 -
Prim算法在找当前最近顶点时使用到了贪婪算法。也叫割边法
一、Prim算法的思想
它是从点的方面考虑构建一颗MST(最小生成树)。
大致思想是:设图G顶点集合为U,首先任意选择图G中的一点作为起始点a,将该点加入集合V,再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小,此时将b点也加入集合V;以此类推,现在的集合V={a,b},再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小,此时将c点加入集合V,直至所有顶点全部被加入V,此时就构建出了一颗MST。
因为有N个顶点,所以该MST就有N-1条边,每一次向集合V中加入一个点,就意味着找到一条MST的边。
构造网(带权图)的最小生成树必须注意两个问题:
(1)尽可能选取权值小的边,但不能构成回路;
(2)选取n-1条恰当的边以连通n个顶点;
二.1、利用图形详细解释Prim算法的思想
Prim算法思想介绍

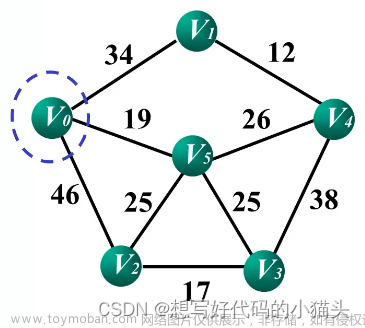
假设刚开始选定的顶点为V1
通过Prim算法 不断在其余各点中找与V1相连的最短权所对应的另一顶点
可以得到 V1-V3=1 为最短权 故把V3并入U中,剩下的点:V2,V4,V5,V6在V-U中 得到下图
(玫红色为已并入MST中的顶点,红色是未被利用的点,后续仍需比较刷新)

由上图可以看到,有很多边可以直接与V1,V3所组成的集合U进行相连(V1-V2,V1-V4,V2-V3,V3-V4,V3-V4,V3-V6)在这些边中找到最小的可以与集合U(即可上图中化红色圈的‘MST’)相连的边,并加入其中,可知,可把 V6加入,V4-V6=4
得到下图

由上图可以看到,经过上一步,V6并入集合U中
有很多边可以直接与V1,V3,V6所组成的集合U进行相连(图中化黑线的边)在这些边中找到最小的可以与集合U(即可上图中化红色圈的‘MST’)相连的边,并加入其中,可把 V4加入,V4-V6=2
得到下图

由上图可以看到,经过上一步,V4并入集合U中
有很多边可以直接与V1,V3,V6所组成的集合U进行相连(图中化黑线的边)在这些边中找到最小的可以与集合U(即可上图中化红色圈的‘MST’)相连的边,并加入其中,可把 V2加入,V4-V3=5
得到下图

可以看到,最后只剩V5没有处理,最后找到V5与此时未构建完全的‘MST’ 相连的权值最小的边,即V2-V5=3
最后
此时按照Prim算法的思想,已经构建完一颗最小生成树
二.2利用图形又又解释Prim算法的思想
此部分转载于博客园 Alan Tu










三、用图示结合代码中重要量进行说明

mstt[i]表示V-U中的节点j到集合U中的最临近点 存在目前建立的MST中
若假设V1为起点,首先进行初始化(采用邻接矩阵实现,所以在实现该功能之前,已经建立了各边之间的关系及其权重)
lowcost[2]=graph[1][2]=6 lowcost[3]=garph[1][3] =1 lowcost[4]=graph[1][4]=5
lowcost[5]=graph[1][5]=∞ lowcost[6]=graph[1][6]=∞
在初始化时 将mst[i]的点都默认为1,mst[i]代表与i节点相连的令一个节点,对应lowcost[i[的起点
mst[2]=1,mst[3]=1,mst[4]=1,mst[5]=1,mst[6]=1 (所有点默认起点是V1,据情况而定)
mst[1]=0,代表1节点已经加入目前在建立的MST
(在后续中,当v3加入后,为表示V3已经加入,mst[3]=0)
明显看出,以V3为终点的边的权值最小=1,所以边<mst[3],3>=1加入MST

此时,因为点V3的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0(在每次更新后,都要把已经加入的点的lowcost[i]设为0),lowcost[4]=5,lowcost[5]=6,lowcost[6]=4(再在这些已经更新过的权中找最小权)
(之前与V1权为的点可以通过与V3相连,更新权值,但注意要更新lowcost[j]的值,在更新过程中,要进行graph[V3][j]与之前的lowcost[j]进行比较,小的重新更新)
mst[2]=3,mst[3]=0,mst[4]=1,mst[5]=3,mst[6]=3
明显看出,以V6为终点的边的权值最小=4,所以边<mst[6],6>=4加入MST

此时,因为点V6的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=2,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=6,mst[5]=3,mst[6]=0
以V4为终点的边 lowcost[2]=2(min),所以边<mst[4],4>=4加入MST

此时,因为点V4的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=0,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=0,mst[5]=3,mst[6]=0
以V2为终点的边 lowcost[2]=5(min),所以边<mst[2],2>=5加入MST

此时,因为点V2的加入,需要更新lowcost数组和mst数组:
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=3,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=2,mst[6]=0
以V5为终点的边 lowcost[5]=3(min) graph[2][5]=3,所以边<mst[5],5>=3加入MST
至此,MST构建成功,如图所示:
此时,两个数组已经变为:
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=0,lowcost[6]=0文章来源:https://www.toymoban.com/news/detail-475636.html
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=0,mst[6]=0文章来源地址https://www.toymoban.com/news/detail-475636.html
四、代码实现(用c语言)
#include<stdio.h>
#include<stdlib.h>
#define VexMax 20
#define Inf 0x7fffffff//32位的最大值 在本程序中代表∞
typedef struct
{
int Vex[VexMax];
int Arc[VexMax][VexMax];
int arcnum, vexnum;
}MGraph;
void Create_G(MGraph* G)//建立该图
{
printf("请输入该图形的顶点数,边数:\n");
scanf("%d,%d", &G->vexnum, &G->arcnum);
printf("请依次输入顶点序号:\n");
for (int i = 1;i <= G->vexnum;i++)//初始化顶点数组 //在初始化的时候,因为已经默认了建立的所有数组下标是从1开始的所以在编写代码的时候要注意范围
{
int m;
printf("第%d个顶点为:", i );
scanf("%d", &m);
G->Vex[i] = m;
}
for(int i=1;i<=G->vexnum;i++)//初始化邻接矩阵,先令所有边的权重为∞ //第一次写的时候,由于i,j的范围没有搞清楚,导致出现很离谱的输出结果
for (int j = 1;j <=G->vexnum;j++)
{
G->Arc[i][j] = G->Arc[j][i] = Inf; //有些代码实现的时候,会令i=j的对角元素置0,因为本人又菜又懒,直接Inf了
}
for (int i = 1;i <=G->arcnum;i++)//按照用户需求。建立边,对边赋值
{
int weight;
int v1, v2;
printf("请输入第%d条的边的邻接点(vi,vj)和对应边的权值:", i);
scanf("%d,%d,%d", &v1, &v2, &weight);
G->Arc[v1][v2] = G->Arc[v2][v1] = weight;//对建立边的邻接矩阵赋值 //这是建立无向图,所以可以G->Arc[v1][v2] = G->Arc[v2][v1],建立有向图的时候要注意不要这样写
}
}
int Prim(int Arc[VexMax][VexMax], int n)//Prim算法
{
int lowcost[VexMax]; //在Prim算法中,要建立两个数组 lowcost[],mst[],记住在循环时要重置更新
int mst[VexMax];
int min = Inf; //这些变量要记得初始化,根据要实现的不同功能,初始化不同的值
int minid = 0;//用来标记可以并入MST中的顶点标号
int sum=0;//用来表示最短路径长度,每次更新完都加上lowcost[i]
//假设从输入的第一个顶点开始构建最小生成树,在该算法中需要两个数组,mst[k],lowcost[k]
//初始化
mst[1] = 0;//表明第一个节点已经在目前正在构建的MST树中
for (int i = 1;i <= n;i++)//在构建MST时,首先要初始化两个数组 //第1个for循环进行初始化,初始化lowcost数组,mst[i]=1
{
lowcost[i] = Arc[1][i];//因为是从第一个顶点开始的直接去遍历之前建立好的邻接矩阵中 第一行,找到与第一个节点相连的边,并把权赋给lowcost[i]
mst[i] = 1;//在初始化的时候,将除第一个节点之外的各节点都设置为mst[i]=1
}
//mst[1] = 0;//表明第一个节点已经在目前正在构建的MST树中 此行顺序无所谓,也可写在上面mst[1]=0显示的位置,只要记住初始化即可
for (int m = 2;m <= n;m++)//遍历其他n-1个点 //第2个for循环 用来构建MST,又包括两个for循环
{
min = Inf; //这个地方要注意,我第一遍写的时候就忘记重置了,得到的结果是一样的
minid = 0; //同理,minid也要重置
for (int i =1;i <= n;i++)//类似于打擂台法,依次进行比较,找到符合条件的,能与现在已经构建的MST中连接的,权值最小的顶点 //第3个for循环,用来找最小的权,把该点信息重置
{
if (lowcost[i] < min && lowcost[i] != 0)
{
min = lowcost[i];
minid = i;//说明此时minid这个点并入MST中
}
}
lowcost[minid] = 0; //!!!!!!!!!要记住 为了防止后续再次被比较,要令该节点的lowcost[minid]=0
sum = sum + min;
printf("v%d-v%d=%d\n",mst[minid],minid,min);//找到一个顶点输出一次
for (int j = 2;j <= n;j++) //第 3个for循环,是为了更新其他顶点的信息
//因为此时又并入了一个顶点,所以还要更新其他顶点的lowcost,取最短的
{
if (Arc[minid][j] < lowcost[j])
{
lowcost[j] = Arc[minid][j];
mst[j] = minid;
}
}
}
return sum;//返回构建完成的最小生成树的最短路径长度
}
int main()
{
int summ;
MGraph G;
Create_G(&G);
summ = Prim(G.Arc, G.vexnum);
printf("最短路径长度为:%d",summ);
system("pause");
return 0;
}到了这里,关于C语言实现Prim算法 —构建最小生成树的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!