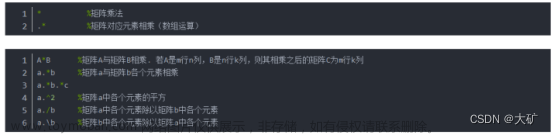
1、所针对的对象:矩阵、阵列;
2、所用运算符:
(1)加减运算:
①、+ :即简单的 A+B 但要求A和B两个矩阵要具有相同的维度;(即两个矩阵行数和列数相同)
例如:

A + B 就是简单的两个矩阵对应位置元素的相加和(A,B都是两行三列矩阵)
而 a + B 报错,因矩阵 a 为三行三列,而矩阵 B 为两行三列(行列数目不一)故不能相加;
②、- :同加法运算
(2)乘法运算
①、矩阵的乘法(*):A * B 其中矩阵 A 的列数应等于矩阵 B 的行数,最后所得矩阵的行数等于矩阵A的行数,所得矩阵的列数等于矩阵B的列数(即,m×n * n×a = m×a)
例如:

②、元素的乘法(.* 点乘):A .* B 矩阵 A 中对用元素与矩阵 B 中对应元素相乘(要求矩阵A与矩阵B行列对应相等)
例如:

(3)除法运算
①、左除( \ ):A \ B(要求矩阵 A 与矩阵 B 的维度相等)

②、点左除(.\):A .\ B 矩阵A中对应元素除以矩阵B中的对应元素(要求矩阵 A 和 B 维度相同)
例如:

文章来源地址https://www.toymoban.com/news/detail-475830.html
③、 右除( / ):A / B(要求矩阵 A 与矩阵 B 的维度相等)
例如:

④、点右除(./):A ./ B 矩阵A中对应元素除以矩阵B中对应元素(要求矩阵A与B维度相等)
例如:

点左除(.\)与点右除(./)当矩阵A点除一个元素时,点左除等价于该元素点右除该矩阵
例如:

点右除为矩阵所有元素都除以该元素
例如:

(4)幂运算
①、矩阵的幂运算:A ^2 相当于A * A(要求A矩阵为方阵,即行数与列数相等)
例如:

②、元素的幂运算:A .^ 2 矩阵A中每一个元素都进行幂运算
例如:

(5)转置运算
矩阵的转置(‘):A’ 即“矩阵A的每一行元素从上往下依次拍成列”
例如:

3、算数运算功能
(1)plus
①、uplus (a) 执行 如C = + A
例如:

②、plus(a,b) 可以执行两个数的加和,也可执行两个矩阵的相加
例如:

(3)minus
①、uminus(a) 类似于uplus(a) 执行如同C = -A
例如:

②、minus(a, b) 执行a - b
例如:

(4)times
①、mtimes(a, b):矩阵相乘,返回的是a * b(矩阵a列数与矩阵b行数相等)
例如:
A = [1 2 3;4 5 6];
B = [2 4;9 16;25 36];
C = mtimes(A,B)
结果为:

②、times(a, b) :元素相乘,返回a .^ b 要求矩阵a,b维度相等

(5)divide
①、rdivide(a, b) :右阵划分,返回 a ./ b (点右除)
例如:

②、ldivide(a, b) :左阵划分,返回 a. b (点左除)
例如:
A = [1 2 3;4 5 6];
B = [2 4 6;8 10 12];
结果为:

③、mrdivide(A, B) :求解线性方程组x * A = B 中的x (A/B)
例如:
A = [1 2 3;4 5 6];
B = [2 4 6;8 10 12];
mrdivide(A,B)
结果为:

④、mldivide(A, B) :求解线性方程组A * x = B 中的x (A\B)
例如:
A = [1 2 3;4 5 6];
B = [2 4 6;8 10 12];
mldivide(A,B)
结果为:
(5)power
①、power(a, b) :矩阵对应元素乘方,返回 a.^b
例如:

②、mpower(a, b) :矩阵的乘方 返回A ^ n (A * A)
例如:

(6)cumprod
①、cumprod(A) :累乘,矩阵第k行元素乘以第k-1行元素
例如:

②、cumprod(A, dim) :沿维 dim 返回返回累积乘积(即m×n维矩阵,若dim = 1,则按照行累乘,若dim = 2,则按照列累乘)
例如:

(7)cumsum
①、cumsum(A) :累加总和,第k行元素等于该行元素加上第k-1行元素
例如:

②、cumsum(A, dim) :返回沿着dim的元素的累积和 (沿着第dim维累加)
例如:

(8)diff
①、diff(X) :差分和近似导数;计算x相邻元素之间的差异(第k行元素等于第k+1行元素减去该行元素)
例如:

②、diff(X,n) :递归应用n次,导致第n个差异(即,diff(A,2) 与 diff(diff(A))相等)

③、diff(X,n,dim) :它是沿标量dim指定的维数计算的第n个差分函数(沿着第dim维度做差分)
例如:

(9)prod
①、prod(A) :元素的乘积,返回A矩阵元素的乘积(返回一行元素,该行元素等于第一行元素与后几行元素)
例如:

②、prod(A,dim) :沿dim维度返回乘积
例如:

③、prod(A,datatype) :在数据类型指定的类中乘以并返回一个数组
例如:

(10)sum
①、sum(A) :数组元素的总和,返回数组的不同维度的和
例如:

②、sum(A,dim) :沿标量A的维度求和
例如:

③、sum(A, 'native') :在本机数据类型A中执行添加,并返回相同数据类型的答案
例如:

(11)ceil(A) :向正无穷方向舍入,将a元素舍入为大于或等于A的最近整数(小数点后不是四舍五入的原则,有小数点就在整数位加一)
例如:

(12)fix(A) :舍入为零,即将小数点舍去,保留整数位
例如:

(13)floor(A) :向负无穷方向舍入,将a元素舍入为小于或等于a的最近整数,不遵循四舍五入的原则,若为正数,则返回整数位,若为负数,则返回整数位减一
例如:

(14)idivide
①、idivide(a, b) 或idivide(a, b,'fix'):整数除法的舍入选项,与a./b相同,只是分数的商向零舍入到最接近的整数
例如:
若A中不是整数类型
则:

因为向0舍入,且结果均为正数,所以小数点舍去,保留整数;
若为负值
则:


②、idivide(a, b, 'round') :分数的商舍入到最近的整数,如同四舍五入的规则
例如:

③、idivide(A, B, 'floor') :分数商向负无穷大舍入到最接近的整数
例如:

若为负的:


④、idivide(A, B, 'ceil') :分数商向无穷大舍入到最接近的整数
例如:

(15)mod (X,Y) : Y除以 X 后的余数, X 是被除数,Y 是除数
①、对数X与数Y取模
例如:

即 4 ➗ 8 商 0 余 4
②、向量取余
例如:

③、 负数余数
例如:

(算法:其中-6较-4小,且可以整除3,则余数为:-4-(-6) = 2;)
④、若除数为负数
例如:

⑤、mod(X,0) 得 X
例如:

(16)rem (X,Y)
①、正整数和向量与正整数之间的除法与mod类似
②、负数除法,被除数为负,除数为正
例如:

( 算法:商-1得-4-(-3)=-4+3=-1)
③、rem(X,0) 得NaN
例如:

(17)round(X)
①、round(X) 将 X 四舍五入为最近的整数(其中X可为单独得整数,也可为一向量)
例如:

②、round(X,N) 四舍五入到N 位(保留N+1位小数,而四舍五入得规则运用到第N位结束,第N+1位是0)
例如:

③、round(X,N) 若N为负数(向左数 |N| 位,该数大于5,该数得前一位加1,从该数起,后面的全为0,且省去小数位)
例如:

(其中,N为-2时,向左数两位到3,而3<5故前一位2不进位,保留1200;
N为-1时,向左数一位到9,因为9>5,故前一位3进一,保留1240) 文章来源:https://www.toymoban.com/news/detail-475830.html
到了这里,关于MATLAB基础—算数运算符的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!