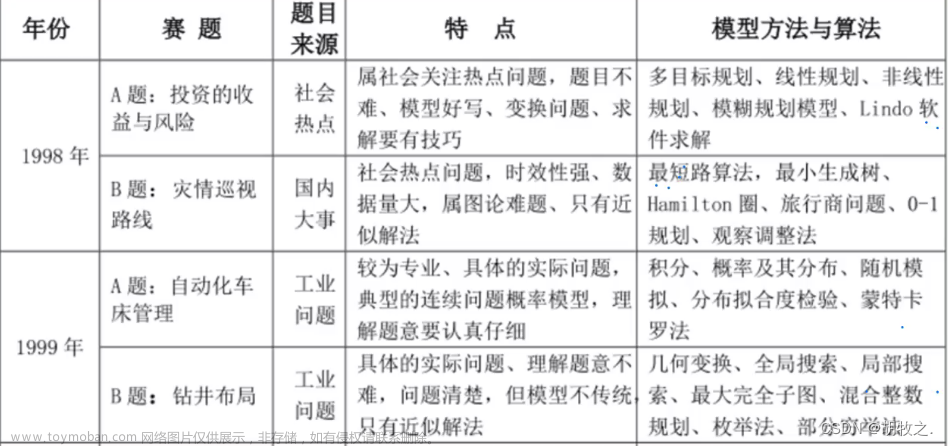
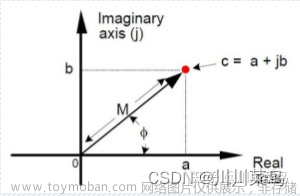
前言
研究对象的机理比较简单，一般用静态、线性、确定性模型就能达到建模目的时，我们基本上可以用初等数学的方法来构造和求解模型。
如果对于某个实际问题，采用初等方法和高级方法建立的两个模型的应用效果相差无几时，，初等方法更受欢迎。
一、双层玻璃窗功效
1.问题背景
2.问题假设
（1）热量传播只有传导，没有对流
（2）
T
1
T_1
T1，
T
2
T_2
T2不变，热传导过程处于稳态
（3）材料均匀，热传导系数为常数
3.模型建立
Q
1
、
Q
2
Q_1、Q_2
Q1、Q2所研究的是单位面积下的情况
T
a
、
T
b
T_a、T_b
Ta、Tb为中间量，通过三个式子可以将其消除，得到不含
T
a
、
T
b
T_a、T_b
Ta、Tb的式子
h
=
l
d
h=\frac{l}{d}
h=dl，将式子用一个量来表示，从而化简式子，使得结果更加直接明了
4.模型应用与结果分析
二、划艇比赛的成绩
1.问题背景
2.问题分析
由机理出发
3.问题假设
艇长为
l
l
l，艇宽为
b
b
b
v
v
v为常数，才可以建立等式
考虑到桨手的特征，体重与功率的相关
4.模型建立
5.模型检验
使用最小二乘法之前，先对式子两边同时取对数，得到一个与模型相吻合的式子:
l
n
t
=
l
n
a
+
b
∗
l
n
n
ln\ t=ln\ a+b*ln\ n
ln t=ln a+b∗ln n
令
a
′
a^{'}
a′等于
l
n
a
ln\ a
ln a
得到下方式子
不妨再令
Y
=
l
n
t
、
X
=
l
n
n
Y=ln\ t、X=ln\ n
Y=ln t、X=ln n
就得到了形如
Y
=
a
′
+
b
∗
X
Y=a^{'}+b*X
Y=a′+b∗X的式子，对其使用最小二乘法
在matlab中ln(x)用log表示，lg(x)函数用log10表示
回代，注意此时求出的仅仅是 a ′ a^{'} a′，而非 a a a
也可直接使用CFTOOL工具进行拟合
三、实物交换
1.问题背景
2.问题分析与建模
类似“等高线”
双方满意也就是双方的满意程度相同
假设交换前双方物品的价值相同，根据CD交换的方案满足等价交换原则，双方交换后物品的价值不变
四、汽车刹车距离与道路通行能力
1.问题背景
2.问题分析与假设
3.模型假设
4.模型建立
1000
v
1000v
1000v作用是换算
k
m
km
km为
m
m
m，该式子表示安全条件下，
1
h
1h
1h内通过断面的最大车辆数
v = d 0 c 2 v=\sqrt{\frac{d_0}{c_2}} v=c2d0是由对勾函数确定的最值
五、估计出租车总数
1.问题背景
2.问题分析
3.模型建立
由于顺序发放，所以总体平均值与总体中位数相同
注意一下的编号均从1开始，而非从0101开始，要换算
假设
x
n
x_n
xn不是最后一个，其后依然有一个
x
x
x，且间隔由之前的平均间隔表示
假设样本点均匀分布于总体中
4.计算与分析
5.数值模拟
六、评选举重总冠军
1.问题背景
2.数据收集
3.数据分析
4.模型建立
5.小结
七、解读CPI
1.问题背景
2.按时间顺序解读CPI
关系：知三求一
可以理解为累积价格指数的特例
3.按分类结构解读CPI
化为矩阵
最小二乘解
八、核军备竞赛
1.问题背景
2.模型假设
3.模型建立
由威慑值
y
0
y_0
y0和当前
x
x
x可能的范围确定出
y
y
y合理的值
当满足
x
=
a
y
x=ay
x=ay时，可以得到一个简洁的式子：
y
=
y
0
s
x
y
y=\frac{y_0}{s^{\frac{x}{y}}}
y=syxy0
这个也就是上述安全曲线的来源
4.模型解释（分析各类可能的变化情况）
九、扬帆远航
1.问题背景
2.模型分析与假设
对力进行分解，主要考虑风对帆的力和对整个船体的力，此时未考虑水的阻力
值得注意的是，假设中将垂直于船身的力忽略，视其被舵所抵消
v
=
k
1
(
f
1
−
P
1
)
v=k_1(f_1-P_1)
v=k1(f1−P1)
表示一种直观关系
3.模型建立与求解
无约束的优化问题
十、节水洗衣机
1.问题背景
2.问题分析
3.模型假设
4.模型建立
轮数不多，可枚举轮数，计算每种情况下的加水量
脱水后，相较于要添加的水，残余的水很少，所以可以进行简化，忽略
c
c
c
5.模型求解
文章来源：https://www.toymoban.com/news/detail-476107.html
6.模型讨论
文章来源地址https://www.toymoban.com/news/detail-476107.html
到了这里，关于数学建模笔记（四）：初等模型的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
