SVM——《统计学习方法第七章》

为什么叫支持向量机

在第二章中我们学过感知机，它是最小化所有误分类点到超平面的距离之和， M 为误分类点的集合，得到的分离超平面是不唯一的。
$$\underset{\omega ,b}{\min }[-\sum _{x_i\in M}{y}_i(\omega \cdot x_i+b)]$$
在支持向量机中，
$$\{\begin{array}{l}分类确信度\frac{|\omega \cdot x_i+b|}{||\omega ||}\\ 分类正确性y_i(\omega \cdot x_i+b)\end{array}\Rightarrow 几何间隔{\gamma }_i=\frac{y_i(\omega \cdot x_i+b)}{||\omega ||}$$
哪些样本最有用？就是几何间隔最小的点$\min {\gamma }_i$。
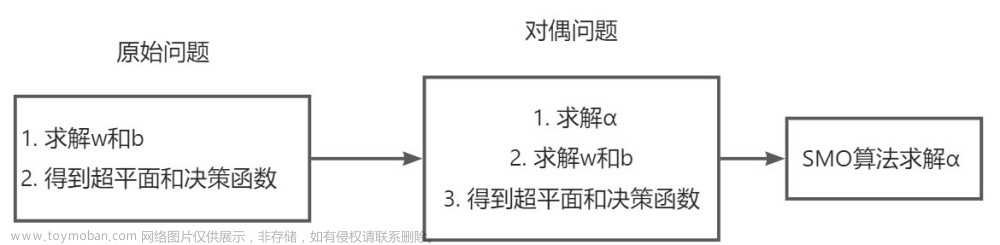
然后使得几何间隔最小的点最大${\max }_{\omega ,b}\min {\gamma }_i$，一看这形式就知道要使用到最大熵章节讲到的原始问题和对偶问题。
$R^n$空间中点和向量是等价的，最有用的那些点$\min {\gamma }_i$称为支持向量。

线性可分支持向量机

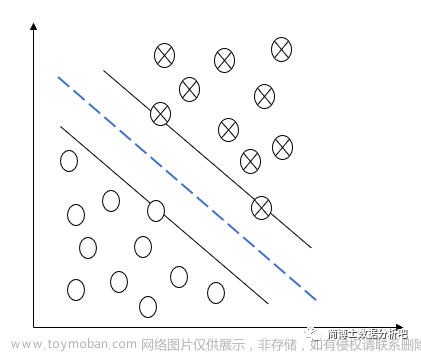
线性可分支持向量机是可以将样本点完全分类开来，但是这种情况在现实中是很少的，但是它是最简单的支持向量机。我们先理清它的过程，还有一些证明，后面的向量机都是在它的基础上发展的。
假设有 N 个样本，M 个特征 ，Y 只有正类（+1）和负类（-1）

几何间隔和函数间隔

几何间隔的定义（点$(x_i,y_i)$到超平面$\omega \cdot x+b=0$的距离）：
$$\begin{array}{rl}{\gamma }_i& =\frac{|\omega \cdot x_i+b|}{||\omega ||}\\ & =\frac{y_i(\omega \cdot x_i+b)}{||\omega ||}\\ & =y_i(\frac{\omega }{||\omega ||}\cdot x_i+\frac{b}{||\omega ||})\end{array}$$
几何间隔的最小值$\gamma ={\min }_i{\gamma }_i$
优化问题为：
$$\begin{array}{rl}& \underset{\omega ,b}{\max }\gamma \\ & s.t.y_i(\frac{\omega }{||\omega ||}\cdot x_i+\frac{b}{||\omega ||})\ge \gamma ,i=1,2,...,N\end{array}$$

函数间隔的定义：
$$\begin{array}{rl}{\hat{\gamma }}_i& =|\omega \cdot x_i+b|\\ & =y_i(\omega \cdot x_i+b)\end{array}$$
函数间隔的最小值$\hat{\gamma }={\min }_i{\hat{\gamma }}_i$
优化问题为：
$$\begin{array}{rl}& \underset{\omega ,b}{\max }\hat{\gamma }/||\omega ||\\ & s.t.y_i(\omega \cdot x_i+b)\ge \hat{\gamma },i=1,2,...,N\end{array}$$

怎么将几何间隔和函数间隔联系起来？
第一种：将$\omega$归一化，即$||\omega ||=1$
以下这三种超平面的$\omega ,b$不一样，但是表示的是同一个超平面。
$$\begin{gathered} 3x^{(1)}+4x^{(2)}+1=0 \\ 6x^{(1)}+8x^{(2)}+2=0 \\ \frac{3}{5}{x}^{(1)}+\frac{4}{5}{x}^{(2)}+\frac{1}{5}=0 \end{gathered}$$
将$\omega$归一化后，函数间隔和几何间隔就是等价的，此时优化问题为：
$$\begin{array}{rl}& \underset{\omega ,b}{\max }\hat{\gamma }/||\omega ||\\ & s.t.\{\begin{array}{l}{y}_i(\omega \cdot x_i+b)\ge \hat{\gamma },i=1,2,...,N\\ ||\omega ||=1\end{array}\end{array}$$

第二种：对$\hat{\gamma }$做处理，和刚刚三个超平面处理类似，对$\omega ,b$进行放缩，可以使得$\hat{\gamma }={\min }_i{\hat{\gamma }}_i=1$
此时优化问题为：
$$\begin{array}{rl}& \underset{\omega ,b}{\min }||\omega ||\\ & s.t.y_i(\omega \cdot x_i+b)\ge 1,i=1,2,...,N\end{array}$$

显然，第二种处理能使得问题更加简单。

证明分离超平面存在且唯一

目标函数是凸函数，约束条件是放射函数，所以这个凸优化问题存在最优解。
现在证最优解是唯一的（反证法）：

原始问题算法流程

输入：数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } ， y i ∈ { + 1 , − 1 } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}，y_i\in \{+1,-1\} T={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}，yi​∈{+1,−1}
输出：最大间隔分离超平面与决策函数

1. 构造优化问题

$$\begin{array}{rl}& \underset{\omega ,b}{\min }\frac{1}{2}||\omega |{|}^2\\ & s.t.1-y_i(\omega \cdot x_i+b)\le 0,i=1,2,...,N\end{array}$$
所得解为${\omega }^{\ast },b^{\ast }$

2. 分离超平面

$${\omega }^{\ast }\cdot x+b^{\ast }=0$$
决策函数
$$f(x)=\mathrm{sign}({\omega }^{\ast }\cdot \mathrm{x}+{\mathrm{b}}^{\ast })$$

对偶算法

推导对偶优化问题

由$\alpha$推导$\omega$和 b

对偶算法流程

输入：数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } ， y i ∈ { + 1 , − 1 } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}，y_i\in \{+1,-1\} T={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}，yi​∈{+1,−1}
输出：最大间隔分离超平面与决策函数

1. 构造优化问题

$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i\ge 0,i=1,2,...,N\end{array}$$

2. 求解优化问题，得到最优解

$${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_N^{\ast }{)}^T$$

3. 根据${\alpha }^{\ast }$得到

$${\omega }^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$$
找到符合${\alpha }_j^{\ast }>0$的点$(x_j,y_j)$,计算
$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j)$$

4. 分离超平面

$${\omega }^{\ast }\cdot x+b^{\ast }=0$$
决策函数
$$f(x)=\mathrm{sign}({\omega }^{\ast }\cdot \mathrm{x}+{\mathrm{b}}^{\ast })$$

线性支持向量机(不完全可分)

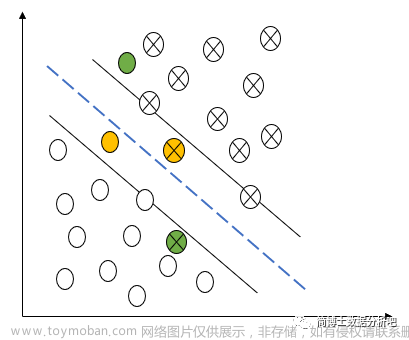
引入松弛因子

在线性支持向量机中，有四类点：
正确分类且在分界线外面的点（白色的点）：$y_i(\omega \cdot x_i+b)\ge 1$
分类正确但在超平面与分界线之间的点（黄色的点）：$y_i(\omega \cdot x_i+b)+{\xi }_i\ge 1,{\xi }_i\in (0,1)$
在超平面上的点：$y_i(\omega \cdot x_i+b)+{\xi }_i\ge 1,{\xi }_i=1$
分类错误的点：$y_i(\omega \cdot x_i+b)+{\xi }_i\ge 1,{\xi }_i>1$

解决重点就都集中到了这个关键的参数 ${\xi }_i$ 上，我们给它起名叫做弹性因子或松弛变量。
现在我们就要把原来线性可分的目标函数改成考虑所有松弛变量的新函数，目标函数是：
$$\min \frac{1}{2}||{\omega }^2||+C\sum _{i=1}^N{\xi }_i$$
这里的 $C$ 被称作惩罚系数，它决定了原始参数和松弛变量之间的影响权重。

• $C$越大代表了误分类起到的作用更大，也可以说对误分类的惩罚力度大
• $C$越小代表正确分类的参数作用更大，对误分类的惩罚力度小

原始问题算法流程

1. 构造优化问题

$$\begin{array}{rl}& \underset{\omega ,b,{\xi }_i}{\min }\frac{1}{2}||{\omega }^2||+C\sum _{i=1}^N{\xi }_i\\ & s.t.1-{\xi }_i-y_i(\omega \cdot x_i+b)\le 0,i=1,2,...,N\\ & -{\xi }_i\le 0,i=1,2,...,N\end{array}$$
所得解为${\omega }^{\ast },b^{\ast }$

2. 分离超平面

$${\omega }^{\ast }\cdot x+b^{\ast }=0$$
决策函数
$$f(x)=\mathrm{sign}({\omega }^{\ast }\cdot \mathrm{x}+{\mathrm{b}}^{\ast })$$

对偶算法

推导对偶优化问题

由$\alpha$推导$\omega$和 b

对偶算法流程

输入：数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } ， y i ∈ { + 1 , − 1 } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}，y_i\in \{+1,-1\} T={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}，yi​∈{+1,−1}
输出：最大间隔分离超平面与决策函数

1. 给定惩罚参数$C$,构造优化问题

$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le C,i=1,2,...,N\end{array}$$

2. 求解优化问题，得到最优解

$${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_N^{\ast }{)}^T$$

3. 根据${\alpha }^{\ast }$得到

$${\omega }^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$$
找到符合$0<{\alpha }_j^{\ast }<C$的点$(x_j,y_j)$,计算
$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j)$$

4. 分离超平面

$${\omega }^{\ast }\cdot x+b^{\ast }=0$$
决策函数
$$f(x)=\mathrm{sign}({\omega }^{\ast }\cdot \mathrm{x}+{\mathrm{b}}^{\ast })$$

从合页损失的角度理解线性支持向量机

合页的表达式

软间隔和合页损失

原始优化问题:
$$\underset{\omega ,b,{\xi }_i}{\min }\frac{1}{2}||{\omega }^2||+C\sum _{i=1}^N{\xi }_i$$

令$${\xi }_i=[1-y_i(\omega \cdot x_i+b){]}_{+}=\{\begin{array}{ll}1-y_i(\omega \cdot x_i+b)& {\xi }_i>0\\ 0& {\xi }_i\le 0\end{array}$$
$$\begin{gathered} \underset{\omega ,b,{\xi }_i}{\min }\frac{1}{2}||{\omega }^2||+C\sum _{i=1}^N{\xi }_i \\ =\underset{\omega ,b}{\min }\frac{1}{2}||{\omega }^2||+C\sum _{i=1}^N[1-y_i(\omega \cdot x_i+b){]}_{+} \\ =\underset{\omega ,b}{\min }\sum _{i=1}^N[1-y_i(\omega \cdot x_i+b){]}_{+}+\frac{1}{2C}||{\omega }^2|| \\ =\underset{\omega ,b}{\min }\sum _{i=1}^N[1-y_i(\omega \cdot x_i+b){]}_{+}+\lambda ||{\omega }^2|| \end{gathered}$$
可以理解为最小化合页损失，后面是惩罚项。

三个损失函数的比较

非线性支持向量机

核函数

非线性的也分为可分和不可分两种情况。我们主要看非线性支持向量机(不可分)的情况。
我们需要将非线性转化为线性：原空间的点映射到新空间，用线性支持向量机取解决。
分析线性支持向量机的优化问题，我们可以发现关键计算$(x_i\cdot x_j)$这个内积，其余都是单个数，所以要求新空间是能够计算内积的。
设映射是$\Phi$,
$$z_i=\Phi (x_i),z_j=\Phi (x_j)$$
$$z_i\cdot z_j=\Phi (x_i)\cdot \Phi (x_j)=K(x_i,x_j)核函数$$
有很多映射对应一个核函数，我们不关心具体是什么映射，只关心核函数。
在新空间里$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i$$

如何找到正定核？（$K(x_i,x_i)\ge 0$）
满足以下两个条件：
①$K$是对称函数
② 新空间上的Gram矩阵半正定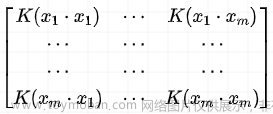

这部分的具体内容需要泛函的知识，难度较大，感兴趣可以看《统计学习方法 李航》

常用核函数(我们所说的核函数就是正定核)：

1. 线性内核函数$K(x_i,x_j)=x_i\cdot x_j$
2. 多项式核函数 $K(x_i,x_j)=(x_i\cdot x_j+1{)}^q$
3. 径向基核函数（高斯核函数，RBF） K ( x i , x j ) = exp ⁡ { − ∣ ∣ x i − x j ∣ ∣ 2 2 σ 2 } K(x_i,x_j)=\exp \{-\frac{||x_i-x_j||^2}{2\sigma^2}\} K(xi​,xj​)=exp{−2σ2∣∣xi​−xj​∣∣2​}

还有一种字符串核函数：

算法流程

和线性支持向量机不同的地方就是将$x_i\cdot x_j$改为$K(x_i,x_j)$。

输入：数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } ， y i ∈ { + 1 , − 1 } T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}，y_i\in \{+1,-1\} T={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}，yi​∈{+1,−1}
输出：最大间隔分离超平面与决策函数

1. 给定惩罚参数$C$,构造优化问题

$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i\\ & s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le C,i=1,2,...,N\end{array}$$

2. 求解优化问题，得到最优解

$${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_N^{\ast }{)}^T$$

3. 根据${\alpha }^{\ast }$得到

$${\omega }^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(\cdot ,x_i)$$
找到符合$0<{\alpha }_j^{\ast }<C$的点$(x_j,y_j)$,计算
$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x_j)$$

4. 分离超平面

$${\omega }^{\ast }\cdot x+b^{\ast }=0$$
决策函数
$$f(x)=\mathrm{sign}({\omega }^{\ast }\cdot \mathrm{x}+{\mathrm{b}}^{\ast })$$

SMO算法

SMO算法用来求解第二步中的优化问题。

坐标下降法（简化优化问题，每次更新一个参数）

SMO算法求α（每次更新两个参数）

更新完两个α后，更新b和Ei

参数的选择

SMO算法流程

文章来源地址https://www.toymoban.com/news/detail-476313.html

到了这里，关于SVM——《统计学习方法第七章》的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！