一、文章说明:
- C++语言实现;
- 有向图的存储结构为: 邻接矩阵;
- 这篇文章的代码是我根据B站UP主懒猫老师所写的,能成功运行,VS里面显示有很多警告。而且还可能存在有未调试出的BUG,请多多指教。
- 观看懒猫老师的视频后,才方便理解博主代码,不然可能理解起来会很吃力。
二、 算法思想与实现思路:
请前往B站观看 up主 懒猫老师 的教学视频;
——附:老师思路清楚,并且通过形象的PPT动画来模拟算法实现过程,非常有利于理解整个算法过程!
视频链接:
1.算法思想:
懒猫老师-数据结构-(46)最短路径(Dijkstra算法,迪杰斯特拉算法,单源最短路径)
2.算法实现过程:
懒猫老师-数据结构-(47)最短路径(Dijkstra算法实现,迪杰斯特拉算法,单源最短路径)
三、3个核心函数:
1.迪杰斯特拉算法函数;
void Dijkstra(AMGraph g)
{
int start;
char c;
cout << "请输入最小路径的源点:" << "\t";
cin >> c;
start = g.Locate_vex(c); //利用定位函数查找源点在顶点表当中的序号;
//1.用动态分配的方式,为路径path, 路径权值dist, 算法思想中的S数组开辟空间。
//注意这里path,dist,S数组单元的序号所对应的顶点和类 AMGraph中顶点表 vexs 所对应的顶点是一样的!
int* path = new int[g.vexnum]; //空间大小为 图的顶点个数,vexnum;
int* dist = new int[g.vexnum];
int* S = new int[g.vexnum];
//2. 初始化这三个数组;
for (int i = 0; i < g.vexnum; i++)
{
dist[i] = g.arcs[start][i];
if (dist[i] != Maxlnt) path[i] = start;
else path[i] = -1;
}
for (int i = 0; i < g.vexnum; i++)
{
S[i] = 0; // 0代表未进入算法思想的S集合,1代表已经进入。
}
S[start] = 1; // 将源点加入S集合。
int num = 1; //计数变量,循环控制条件;
int min;
//3. 正式进入算法,求源点到其它顶点的最短路径。
while (num < g.vexnum)
{
min = findMinDist(dist, S, g.vexnum); //查找在当前顶点所邻接后继结点的边中,具有最小权值的后继结点的序号。
S[min] = 1;
for (int i = 0; i < g.vexnum; i++) //对路径数组path 和路径权值数组dist 进行更新。
{
if ((S[i] == 0) && (dist[i] > dist[min] + g.arcs[min][i]))
{
dist[i] = dist[min] + g.arcs[min][i];
path[i] = min;
}
}
num++;
}
displayPath(dist, path, start, g);
delete[]path;
delete[]dist;
delete[]S;
}
2.findMinDist()函数;
函数功能:
查找当前结点与后继邻接顶点中具有最小权值的边,的邻接顶点的序号
int findMinDist(int dist[], int S[], int n)
{
int MIN = Maxlnt + 1;
int mark = -1;
for (int i = 0; i < n; i++)
{
if (S[i] == 0)
{
if (dist[i] < MIN)
{
MIN = dist[i];
mark = i;
}
}
}
return mark;
}
3. 路径输出函数displayPath();
函数功能:
- 一、如果对于除了源点的其它顶点,如果源点是可达该顶点的,则输出其的最小路径和权值
- 二、输出源点所到达不了的顶点,说明这源点和这个顶点之间不存在有最短路径。
void displayPath(int dist[], int path[], int start, AMGraph g)
{
char* road = new char[g.vexnum];
int number; //number 用来表示源点到第i号顶点路径的长度;
for (int i = 0; i < g.vexnum; i++)
{
int j = i; //这里j可以从充当一个指针,一开始指向每条路径的终点。
if (j != start && dist[j] != Maxlnt) //注意这里j指向的终点必须是可达源点的,所以要加上判断条件 dist[j] 不可以等于无穷大 Maxlnt ;
{
number = -1;
//1.利用while循环,从最短路径的终点向源点逐步衍生,逐步扩大road数组
while (g.vexs[j] != g.vexs[start]) //当j 指向源点的时候,循环结束。
{
number++;
road[number] = g.vexs[j];
j = path[j]; //j指向当前顶点的,前驱邻接顶点。
if (j == start) //如果 j 指向源点了,将源点加入road 数组,数组中存储的就是逆序的路径了,number为路径的长度。
{
number++;
road[number] = g.vexs[j];
}
}
//2.利用for循环,将路径数组逆序输出即可得到 源点到第 i 号顶点的最小路径。
cout << endl << g.vexs[start] << " to " << g.vexs[i] << " " << "路径权值:" << dist[i] << "\t" << "路径为: ";
for (int k = number; k >= 0; k--)
{
if (k == 0)
{
cout << road[k] << endl;
}
else cout << road[k] << "—>";
}
cout << endl;
}
}
//3.布尔变量adjust, 用来判断源点是否有到达不了的顶点, 如果有则利用for循环输出。
bool adjust = true;
for (int i = 0; i < g.vexnum; i++)
{
if (dist[i] == Maxlnt)
{
adjust = false;
break;
}
}
if (adjust == false)
{
cout << endl << "源点:" << g.vexs[start] << "到达不了的顶点为:" << "\t";
for (int i = 0; i < g.vexnum; i++)
{
if (dist[i] == Maxlnt)
cout << g.vexs[i] << "\t";
}
cout << endl << endl;
}
delete[]road;
}
四、完整代码:
说明: 为了更方便地调试程序,我将算法具体实现写成了一个小小系统的形式,
所以代码会比较冗长,注释也比较多,阅读起来可能很不舒适。
#include<iostream>
#include<string>
using namespace std;
#define Maxlnt 32767
#define MVNum 20
#define OK 1
class AMGraph
{
private:
char vexs[MVNum]; //顶点表;
int arcs[MVNum][MVNum]; //边表;
int vexnum, arcnum; //点的数量和边的数量;
public:
bool creat_graph();
int Locate_vex(char c); //顶点定位函数,定位顶点在顶点表当中的数字;
void print(); // 图的信息打印函数;
friend void displayPath(int dist[], int path[], int start, AMGraph g); // 路径输出函数;
friend void Dijkstra(AMGraph g);
};
int AMGraph::Locate_vex(char c)
{
for (int i = 0; i < vexnum; i++)
{
if (c == vexs[i]) return i;
}
return -1;
}
bool AMGraph::creat_graph()
{
cout << "请依次输入图的顶点数目和边数:" << "\t";
cin >> vexnum >> arcnum;
cout << endl << "请依次输入" << vexnum << "个顶点:" << "\t";
for (int i = 0; i < vexnum; i++)
{
cin >> vexs[i];
}
for (int i = 0; i < vexnum; i++)
{
for (int j = 0; j < vexnum; j++)
{
if (i == j) arcs[i][j] = 0;
else arcs[i][j] = Maxlnt;
}
}
cout << endl;
for (int k = 0; k < arcnum; k++)
{
char v1, v2;
int w;
cout << "请分别输入第" << k + 1 << "条有向边的起点,终点和权值:" << "\t";
cin >> v1 >> v2 >> w;
int i = Locate_vex(v1);
int j = Locate_vex(v2);
arcs[i][j] = w;
}
return OK;
}
void AMGraph::print()
{
cout << endl << "顶点表的信息:" << endl;
for (int i = 0; i < vexnum; i++)
{
cout << vexs[i] << " ";
}
cout << endl << endl;
cout << "邻接矩阵的信息为:" << endl;
// 这里for循环 从-1 开始打印邻接矩阵表格;
for (int i = -1; i < vexnum; i++)
{
for (int j = -1; j < vexnum; j++)
{
//i=-1的时候, 需要输出边表中, 以i为起点的边所对应的终点;
if (i == -1)
{
if (j == -1)cout << " " << "\t";
else cout << vexs[j] << "\t";
if (j == vexnum - 1) //换行条件控制
cout << endl;
}
else
{
//j=-1的时候,需要输出边表中, 以j为终点的边所对应的起点:
if (j == -1)cout << vexs[i] << "\t";
else
{
if (arcs[i][j] == Maxlnt)
cout << "∞" << "\t";
else cout << arcs[i][j] << "\t";
if (j == vexnum - 1) //换行条件控制
cout << endl;
}
}
}
}
}
int findMinDist(int dist[], int S[], int n)
{
int MIN = Maxlnt + 1;
int mark = -1;
for (int i = 0; i < n; i++)
{
if (S[i] == 0)
{
if (dist[i] < MIN)
{
MIN = dist[i];
mark = i;
}
}
}
return mark;
}
void displayPath(int dist[], int path[], int start, AMGraph g)
{
char* road = new char[g.vexnum];
int number; //number 用来表示源点到第i号顶点路径的长度;
for (int i = 0; i < g.vexnum; i++)
{
int j = i; //这里j可以从充当一个指针,一开始指向每条路径的终点。
if (j != start && dist[j] != Maxlnt) //注意这里j指向的终点必须是可达源点的,所以要加上判断条件 dist[j] 不可以等于无穷大 Maxlnt ;
{
number = -1;
//1.利用while循环,从最短路径的终点向源点逐步衍生,逐步扩大road数组
while (g.vexs[j] != g.vexs[start]) //当j 指向源点的时候,循环结束。
{
number++;
road[number] = g.vexs[j];
j = path[j]; //j指向当前顶点的,前驱邻接顶点。
if (j == start) //如果 j 指向源点了,将源点加入road 数组,数组中存储的就是逆序的路径了,number为路径的长度。
{
number++;
road[number] = g.vexs[j];
}
}
//2.利用for循环,将路径数组逆序输出即可得到 源点到第 i 号顶点的最小路径。
cout << endl << g.vexs[start] << " to " << g.vexs[i] << " " << "路径权值:" << dist[i] << "\t" << "路径为: ";
for (int k = number; k >= 0; k--)
{
if (k == 0)
{
cout << road[k] << endl;
}
else cout << road[k] << "—>";
}
cout << endl;
}
}
//3.布尔变量adjust, 用来判断源点是否有到达不了的顶点, 如果有则利用for循环输出。
bool adjust = true;
for (int i = 0; i < g.vexnum; i++)
{
if (dist[i] == Maxlnt)
{
adjust = false;
break;
}
}
if (adjust == false)
{
cout << endl << "源点:" << g.vexs[start] << "到达不了的顶点为:" << "\t";
for (int i = 0; i < g.vexnum; i++)
{
if (dist[i] == Maxlnt)
cout << g.vexs[i] << "\t";
}
cout << endl << endl;
}
delete[]road;
}
void Dijkstra(AMGraph g)
{
int start;
char c;
cout << "请输入最小路径的源点:" << "\t";
cin >> c;
start = g.Locate_vex(c); //利用定位函数查找源点在顶点表当中的序号;
//1.用动态分配的方式,为路径path, 路径权值dist, 算法思想中的S数组开辟空间。
//注意这里path,dist,S数组单元的序号所对应的顶点和类 AMGraph中顶点表 vexs 所对应的顶点是一样的!
int* path = new int[g.vexnum]; //空间大小为 图的顶点个数,vexnum;
int* dist = new int[g.vexnum];
int* S = new int[g.vexnum];
//2. 初始化这三个数组;
for (int i = 0; i < g.vexnum; i++)
{
dist[i] = g.arcs[start][i];
if (dist[i] != Maxlnt) path[i] = start;
else path[i] = -1;
}
for (int i = 0; i < g.vexnum; i++)
{
S[i] = 0; // 0代表未进入算法思想的S集合,1代表已经进入。
}
S[start] = 1; // 将源点加入S集合。
int num = 1; //计数变量,循环控制条件;
int min;
//3. 正式进入算法,求源点到其它顶点的最短路径。
while (num < g.vexnum)
{
min = findMinDist(dist, S, g.vexnum); //查找在当前顶点所邻接后继结点的边中,具有最小权值的后继结点的序号。
S[min] = 1;
for (int i = 0; i < g.vexnum; i++) //对路径数组path 和路径权值数组dist 进行更新。
{
if ((S[i] == 0) && (dist[i] > dist[min] + g.arcs[min][i]))
{
dist[i] = dist[min] + g.arcs[min][i];
path[i] = min;
}
}
num++;
}
displayPath(dist, path, start, g);
delete[]path;
delete[]dist;
delete[]S;
}
void menu()
{
cout << "****《迪杰斯特拉算法求最短路径》*****" << endl;
cout << "**1. 图的建立" << endl;
cout << "**2. 输出图的信息" << endl;
cout << "**3. 求图的最短路径" << endl;
cout << "**4. 退出" << endl;
cout << "____________________________________________" << endl;
}
void deletescreen()
{
system("pause");
system("cls");
}
int main()
{
void menu();
void deletescreen();
AMGraph g1;
//menu();
string choose;
while (true)
{
menu();
cin >> choose;
if (choose == "1")
{
g1.creat_graph();
cout << endl << "图建立成功!" << endl;
deletescreen();
}
else if (choose == "2")
{
g1.print();
deletescreen();
}
else if (choose == "3")
{
Dijkstra(g1);
deletescreen();
}
else if (choose == "4")
{
cout << "退出成功!" << endl;
exit(0);
}
else
{
cout << "输入有误!请重新输入" << endl;
deletescreen();
}
}
return 0;
}
五、测试情况:
测试一:
求图片中
1.源点为A到其它顶点的最小路径
2.源点为D到其它顶点的最小路径
测试结果:
1.建图
2.图的信息:
3.A到其它顶点的最小路径
4.D到其它顶点的最小路径
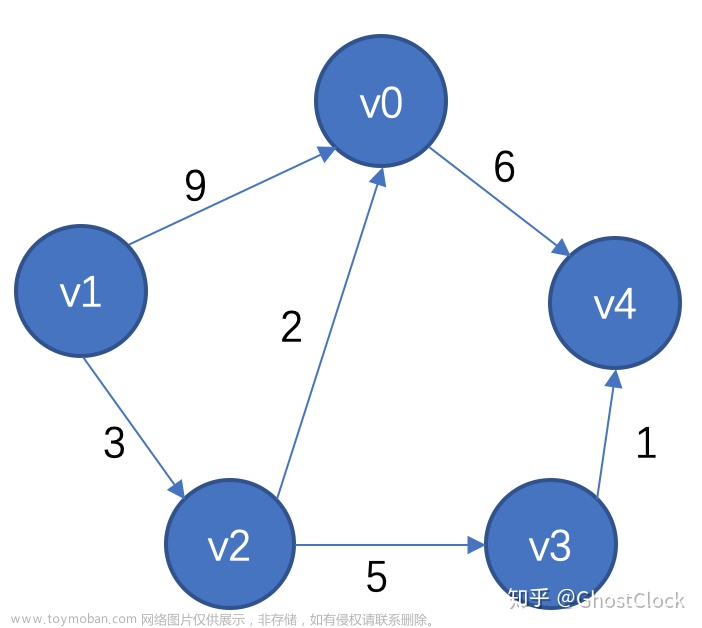
测试二:
1.测试案例:
2.求以 0 作为源点,到其它顶点的最短路径: 文章来源:https://www.toymoban.com/news/detail-477234.html
文章来源:https://www.toymoban.com/news/detail-477234.html
感谢你的收看,希望这可以帮助到你。文章来源地址https://www.toymoban.com/news/detail-477234.html
到了这里,关于Dijkstra算法实现求有向图中一顶点到其余各个顶点的最短路径的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!