二叉树的相关操作-Toy模板网

这篇具有很好参考价值的文章主要介绍了二叉树的相关操作。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

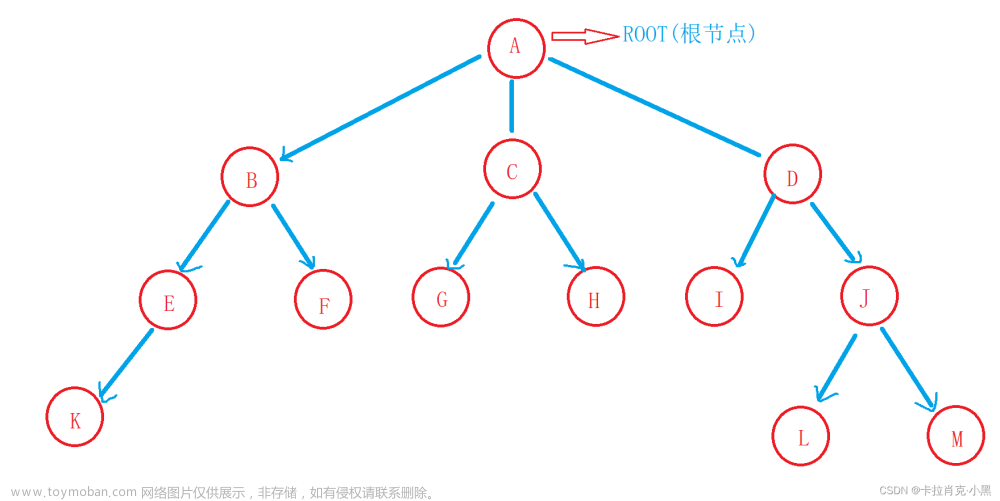
一.二叉树

本文的数据结构基于C语言练习。

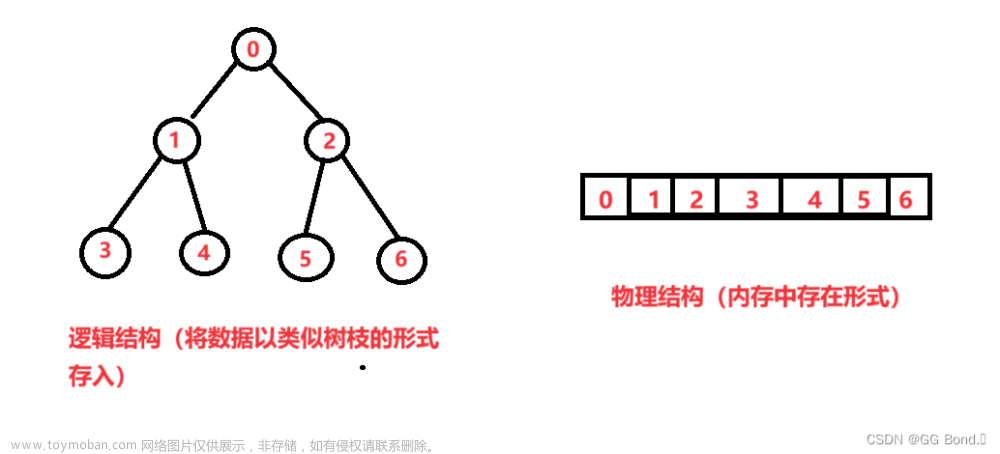
C语言中的二叉树是一种数据结构，用于表示具有层次关系的数据集合。它由一个根节点开始，每个节点最多有两个子节点，分别称为左子节点和右子节点。

二叉树有许多相关性质，其中一些重要的包括：

深度：指从根节点到某个节点的路径长度。树的深度等于所有节点深度的最大值加上1。
高度：指从某个节点到其子树中的最远叶子节点的路径长度。树的高度等于根节点的高度。
节点数：指树中节点的总数。如果树的深度为d，则节点数不超过2^d-1个。
层次遍历：按照从上到下、从左到右的顺序遍历树中的节点。
先序遍历：先访问根节点，然后按照先序遍历左子树和右子树。
中序遍历：先按照中序遍历左子树，然后访问根节点，最后按照中序遍历右子树。
后序遍历：先按照后序遍历左子树和右子树，然后访问根节点。
平衡二叉树：指任意节点的左右子树高度差不超过1的二叉树。
满二叉树：指所有非叶子节点都有两个子节点，且所有叶子节点都在同一层的二叉树。
完全二叉树：指除最后一层之外，每一层都被填满的二叉树，最后一层从左到右填充。

二.二叉树的遍历

这里通过一个例子来详细介绍：

2023/6/8 09:49:27

二叉树遍历是指按照某个顺序依次访问二叉树的每一个节点，目前比较常用的三种遍历分别是先序遍历、中序遍历和后序遍历。下面举例介绍这三种遍历：

假设有如下一棵二叉树：

其中节点1为根节点，节点2和3为节点1的子节点，节点4和5为节点2的子节点。

先序遍历：

先序遍历指先访问根节点，然后按先序遍历左子树和右子树。对于上述二叉树的先序遍历结果为：1, 2, 4, 5, 3。具体方法是从根节点出发，先输出根节点1，然后递归地遍历左子树2和右子树3，对于左子树2，先输出它的根节点2，然后递归遍历它的左子树4和右子树5。

中序遍历：

中序遍历指按照中序遍历左子树、访问根节点和中序遍历右子树的顺序来遍历二叉树。对于上述二叉树的中序遍历结果为：4, 2, 5, 1, 3。具体方法是先递归遍历左子树2，输出节点4和2，再输出根节点1，最后递归遍历右子树3，输出节点5。

后序遍历：

后序遍历指按照后序遍历左子树、后序遍历右子树和访问根节点的顺序来遍历二叉树。对于上述二叉树的后序遍历结果为：4, 5, 2, 3, 1。具体方法是先递归遍历左子树2，输出节点4和5，再递归遍历右子树3，输出节点2，最后输出根节点1。

三.线索二叉树

线索二叉树是一种特殊的二叉树，其每个节点都附带了指向其前驱和后继节点的线索，这些线索可以加速对节点的遍历操作。在线索二叉树中，若左子树存在，则左子树的最右下节点的右孩子会指向该节点的后继节点；若右子树存在，则右子树的最左下节点的左孩子会指向该节点的前驱节点。

线索二叉树的遍历分为前序、中序、后序和按照线索遍历四种方式，下面我们以中序遍历为例进行介绍。

假设有如下一棵二叉树：

其中节点1为根节点，节点2和3为节点1的子节点，节点4和5为节点2的子节点。

对于线索二叉树，我们需要首先将其转换成线索二叉树，过程如下：

先建立一个头结点，其中头结点的左孩子指向根节点，右孩子指向中序遍历的最后一个节点。
对于每一个节点，如果其左孩子不存在，则将其左孩子设置为前驱节点，并将前驱节点的右孩子指向该节点。如果其右孩子不存在，则将其右孩子设置为后继节点，并将后继节点的左孩子指向该节点。
对根节点进行中序遍历，递归地对左子树进行线索化，然后处理其前驱指针，随后递归地对右子树进行线索化，然后处理其后继指针。

转换成线索二叉树之后，我们可以使用中序遍历来遍历整棵树。具体方法是从头结点开始，依次访问每个节点的后继节点，直到遇到尾节点即可结束遍历。

对于上述例子，通过中序遍历得到的节点顺序为：4, 2, 5, 1, 3。而在线索二叉树中，4的后继节点是2，2的后继节点是5，5的后继节点是1，1的后继节点是3，最后3的后继节点是尾节点，因此我们依次输出4、2、5、1、3就完成了中序遍历。

四.核心功能实现

1.初始构造一棵二叉树

//我们先初始化构造一个二叉树
void InitBTree(BTnode &T){                  //T是一个结构体指针，指向这个树结点的结构体，而这个结构体又包含两个指针
	T=(BTnode)malloc(sizeof(BTree));
	T->data=50;
	T->lchild=NULL;
	T->rchild=NULL;
	T->ltag=T->rtag=0;
}

//插入一个树结点
void Insert(BTnode &T,int x){             //这里x是我们插入结点需要保存的值
	if(T == NULL){ // 最后结点为空，插入节点
		T = (BTnode)malloc(sizeof(BTree));
		T->data = x;
		T->lchild = NULL;
		T->rchild = NULL;
		T->ltag=T->rtag=0;
	}
	else{
		if(x <= T->data){ // 插入左子树
			Insert(T->lchild, x);
		}
		else{ // 插入右子树
			Insert(T->rchild, x);
		}
	}
}

2.普通二叉树的递归遍历

//访问，也就是输出函数
void Visit(BTnode &T){
	printf("%d\t",T->data);
}

//先序遍历
void Preorder(BTnode &T){
	if(T!=NULL){
		Visit(T);        //在访问函数里面定义我们想要的可视化输出
		Preorder(T->lchild);
		Preorder(T->rchild);
	}
}

//中序遍历
void Inorder(BTnode &T){
	if(T!=NULL){
		Inorder(T->lchild);
		Visit(T);
		Inorder(T->rchild);
	}
}

//后序遍历
void Postorder(BTnode &T){
	if(T!=NULL){
		Postorder(T->lchild);
		Postorder(T->rchild);
		Visit(T);
	}
}

3.二叉树线索化

//中序遍历线索化
void InThread(BTnode &p,BTnode &pre){
	if(p!=NULL){
		InThread(p->lchild,pre);
		if(p->lchild==NULL){
			p->lchild=pre;             //中序遍历左孩子就是根结点的前驱
			p->ltag=1;
		}
		if(pre!=NULL && pre->rchild==NULL){           //刚刚建立了这个结点的前驱，那前驱结点的后继不就是该结点吗
			pre->rchild=p;
			pre->rtag=1;
		}
		pre=p;                   //这个结点标记完了，换下一个
		//中间这一部分可以改写成visit函数，你就看出来这个简单的递归了
		InThread(p->rchild,pre);
	}
}
/*这只是针对某一个结点线索化的处理过程*/

//构造中序线索二叉树
void createITree(BTnode &T){          //调用刚刚线索化的方法来改造我们原来的二叉树
	BTnode pre=NULL;                //刚开始假设没有pre则为NULL
	if(T!=NULL){
		InThread(T,pre);                //把二叉树进行线索化
		pre->rchild=NULL;               //处理最后一个结点
		pre->rtag=1;
	}
	
}

4.线索二叉树的遍历

//该函数用来找二叉树中序序列的第一个结点
BTNode *Firstnode(BTnode &p){
	while(p->ltag==0)              //第一个结点没有前驱结点，所以其lchild=0，其余原本左孩子为空的结点都变成了左线索
		p=p->lchild;
	return p;
}

//该函数用来找后继结点
BTNode *Nextnode(BTnode &p){
	if(p->rtag==0)
		return Firstnode(p->rchild);      //rtag=0说明还是右孩子，找右子树中的第一个结点为其后继
	else
		return p->rchild;  //ratg=1说明右孩子就是后继，直接返回
}

//最后的大招，中序线索二叉树的遍历
void Inorder1(BTnode &T){
	for(BTNode *p=Firstnode(T);p!=NULL;p=Nextnode(p))          //不要for循环只会i+1
		Visit(p);                
}

五.完整代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef struct BTNode{
	int data;                          //为了实验简便，这里存储的数据都为整数
	struct BTNode *lchild,*rchild;
	int ltag,rtag;                   //左右线索标志
}BTree,*BTnode;                       //之所以这样是为了区分结点和树

//我们先初始化构造一个二叉树
void InitBTree(BTnode &T){                  //T是一个结构体指针，指向这个树结点的结构体，而这个结构体又包含两个指针
	T=(BTnode)malloc(sizeof(BTree));
	T->data=50;
	T->lchild=NULL;
	T->rchild=NULL;
	T->ltag=T->rtag=0;
}

//插入一个树结点
void Insert(BTnode &T,int x){             //这里x是我们插入结点需要保存的值
	if(T == NULL){ // 最后结点为空，插入节点
		T = (BTnode)malloc(sizeof(BTree));
		T->data = x;
		T->lchild = NULL;
		T->rchild = NULL;
		T->ltag=T->rtag=0;
	}
	else{
		if(x <= T->data){ // 插入左子树
			Insert(T->lchild, x);
		}
		else{ // 插入右子树
			Insert(T->rchild, x);
		}
	}
}
/*为了方便定义插入规则，我们这里实验二叉排序树的规则即可*/
/*虽然这里用二叉排序树的规则方便了定义插入规则，但复杂了删除操作
  我们这里也只是为了演示二叉树的遍历和线索二叉树，所以不定义删除函数*/

//访问，也就是输出函数
void Visit(BTnode &T){
	printf("%d\t",T->data);
}

//先序遍历
void Preorder(BTnode &T){
	if(T!=NULL){
		Visit(T);        //在访问函数里面定义我们想要的可视化输出
		Preorder(T->lchild);
		Preorder(T->rchild);
	}
}

//中序遍历
void Inorder(BTnode &T){
	if(T!=NULL){
		Inorder(T->lchild);
		Visit(T);
		Inorder(T->rchild);
	}
}

//后序遍历
void Postorder(BTnode &T){
	if(T!=NULL){
		Postorder(T->lchild);
		Postorder(T->rchild);
		Visit(T);
	}
}

/*完成了这几个遍历后，我们要开始构造线索二叉树了*/
/*构造三种线索二叉树，前提是这个树以及存在，我们采用的方法是边遍历边构造*/

//中序遍历线索化
void InThread(BTnode &p,BTnode &pre){
	if(p!=NULL){
		InThread(p->lchild,pre);
		if(p->lchild==NULL){
			p->lchild=pre;             //中序遍历左孩子就是根结点的前驱
			p->ltag=1;
		}
		if(pre!=NULL && pre->rchild==NULL){           //刚刚建立了这个结点的前驱，那前驱结点的后继不就是该结点吗
			pre->rchild=p;
			pre->rtag=1;
		}
		pre=p;                   //这个结点标记完了，换下一个
		//中间这一部分可以改写成visit函数，你就看出来这个简单的递归了
		InThread(p->rchild,pre);
	}
}
/*这只是针对某一个结点线索化的处理过程*/

//构造中序线索二叉树
void createITree(BTnode &T){          //调用刚刚线索化的方法来改造我们原来的二叉树
	BTnode pre=NULL;                //刚开始假设没有pre则为NULL
	if(T!=NULL){
		InThread(T,pre);                //把二叉树进行线索化
		pre->rchild=NULL;               //处理最后一个结点
		pre->rtag=1;
	}
	
}
//这样我们就把原来的那棵二叉树改成了线索二叉树，为了查看我们的线索二叉树是否正确，我们又要写对应线索二叉树的方法

/*对线索树进行遍历时，只要先找到序列的第一个结点，然后依次取其后继，知道其后继为空代表整个二叉树遍历完*/
/*这里又有一点，其右线索标志为1，右孩子就指示其后继，但有时候也有其结点原来左右孩子就都不为空，这个时候就选择其右子树中
  第一个访问的结点（右子树中最左下的结点）为其后继*/

//该函数用来找二叉树中序序列的第一个结点
BTNode *Firstnode(BTnode &p){
	while(p->ltag==0)              //第一个结点没有前驱结点，所以其lchild=0，其余原本左孩子为空的结点都变成了左线索
		p=p->lchild;
	return p;
}

//该函数用来找后继结点
BTNode *Nextnode(BTnode &p){
	if(p->rtag==0)
		return Firstnode(p->rchild);      //rtag=0说明还是右孩子，找右子树中的第一个结点为其后继
	else
		return p->rchild;  //ratg=1说明右孩子就是后继，直接返回
}

//最后的大招，中序线索二叉树的遍历
void Inorder1(BTnode &T){
	for(BTNode *p=Firstnode(T);p!=NULL;p=Nextnode(p))          //不要for循环只会i+1
		Visit(p);                
}

int main(){
	BTnode T;
	InitBTree(T);
	int nums[]={20,45,68,54,8};   //初始化二叉树待插入的数据,注意我们初始化定义了根结点的值为50
	for(int i=0;i<5;i++){
		Insert(T,nums[i]);
	}
	//到这里我们脑海里应该有了二叉树的画面了
	printf("先序遍历：");
	Preorder(T);
	printf("\n");
	printf("中序遍历：");
	Inorder(T);
	printf("\n");
	printf("后序遍历：");
	Postorder(T);
	printf("\n");
	//这一行下面开始我们转向线索二叉树
	createITree(T);
	printf("中序线索二叉树遍历：");
	Inorder1(T);
}

/*这里提一嘴，学习了栈和队列后，我们知道递归背地里是通过栈来实现的，所以这里的三种遍历我们如果
  不想使用递归，就得使用栈，比较麻烦，为了快速演示，递归虽然效率低但我们还是选择使用它*/