题目
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有 N 种蒸笼,其中第 i 种蒸笼恰好能放 A i个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买 X 个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有 X 个包子。比如一共有 3 种蒸笼,分别能放 3、4 和 5 个包子。当顾客想买 11 个包子时,大叔就会选 2 笼 3 个的再加 1 笼 5 个的(也可能选出 1 笼 3 个的再加 2 笼 4 个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有 3 种蒸笼,分别能放 4、5 和 6 个包子。而顾客想买 7 个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入描述
第一行包含一个整数 (1≤N≤100)。
以下 N 行每行包含一个整数 A i (1≤A i ≤100)。
输出描述
一个整数代表答案。如果凑不出的数目有无限多个,输出 INF。
输入输出样例
示例1
输入
2
4
5
输出
6
样例说明
凑不出的数目包括:1, 2, 3, 6, 7, 11。
示例2
输入
2
4
6
输出
INF
样例说明
所有奇数都凑不出来,所以有无限多个文章来源:https://www.toymoban.com/news/detail-477969.html
分析
- 首先分析一下什么时候凑不出来的数量是 inf ,什么时候不是 inf:
设有方程ax+by=c,其中a,b是笼子能放的包子数目,x,y是笼子的数量,c是能够组合成的包子数量。
假设a,b满足:gcd(a,b)=d,即:(a/d )*(d*x) +(b/d)*(d*y) = c
我们令:m=a/d,n=b/d,就得到:m*d*x+n*d*y=c --> d*(m*x+n*y)=c,这说明得到的c可以被d整除,c是d的整数倍。
-
此时
- 如果d>1,比如d=3,那得到的c必然只能是3的倍数,此时所有不是3的倍数的包子都凑不出来,结果是 inf。
- 如果d=1,那得到的c必然是1的倍数,此时所有是1的倍数的包子都可以凑出来(在x和y可以是负数的情况下),结果不是inf。
因为笼子的数量不能是负数,所以当c大于某一个值时,以后的值都可以凑出来,而小于这个值时,存在凑不出来的情况,这个凑不出来的数目就是我们接下来要求的值。
对于ax+by+...+cz=c,当gcd(a,b,..,z)=1时,结果是非inf。文章来源地址https://www.toymoban.com/news/detail-477969.html
- 动态规划求解:
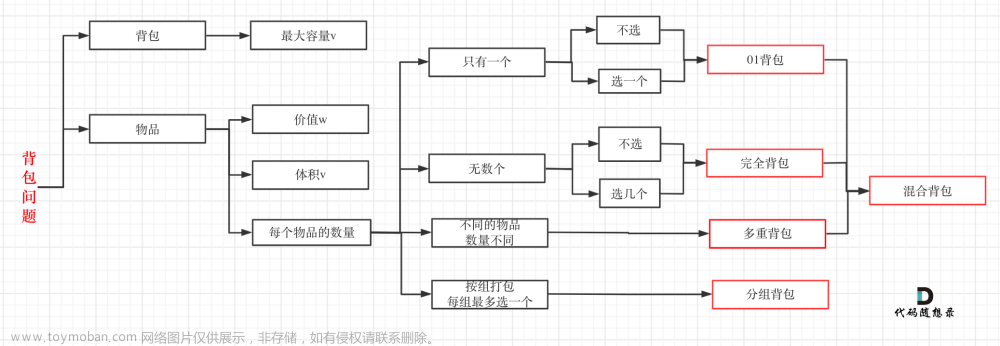
完全背包问题:有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用,第 i 种物品的体积是 vi,价值是 wi。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
很像完全背包问题:有 N 种物品,第 i 种物品的体积是 vi,这些物品的任意次组合恰好可以填满体积是多少的背包。
解法:一维dp
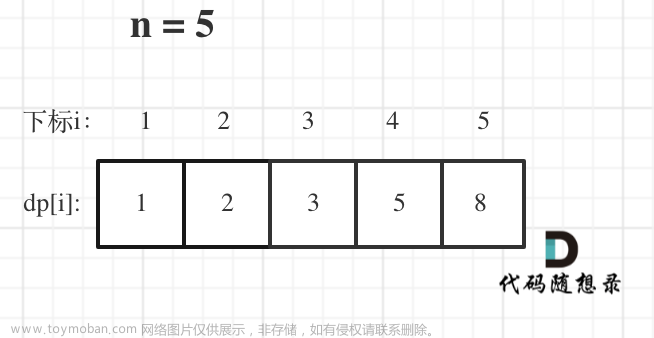
设状态数组dp[]。dp[i]=1表示容量为i的背包可以被恰好填满,dp[i]=0表示容量为i的背包不可以被恰好填满。
状态转移方程:dp[i] = max(dp[i], dp[i-wk]) ,k = 1,2,...,n,且i>wk。
python代码
import math
n = int(input())
num = []
for i in range(n):
num.append(int(input()))
num.sort() # 排序
# dp的最大长度,根据推算以99,100为例子,如果在maxlo*maxlo时还没有达到连续,那以后也不会连续
N = num[-1]*num[-1]+1
# 状态数组dp[i]表示i个包子能否由已有的笼组成,0表示不能,1表示能
dp = [0 for i in range(N)]
dp[0] = 1 # 初始化0个包子可以由0个笼子组成,也是成立的
def gcd(li):
"""求最大公因数"""
g = li[0]
for i in li:
g = math.gcd(g,i)
return g
"""
# 本来用的解包来向math.gcd()传递参数,但是蓝桥杯的python版本不支持解包,每次一用就报错
def gcd(li):
return math.gcd(*li)
"""
if gcd(num)>1: # 如果num里面的数的最大公因数大于1
print("INF")
else:
""" 否则计算有多少数字不能表示"""
# 首先利用dp计算能表示那些数
for i in range(N): # 从dp[0]到dp[maxdp]
for dig in num: # 状态转移方程种的wk项
if dig >i:
break
dp[i] = max(dp[i],dp[i-dig])
# 然后把总的数减去能表示的数就是不能表示的数
print(N-sum(dp))
Java代码
package demo.test1;
import java.math.BigInteger;
import java.util.*;
public class test1 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] num = new int[n];//放笼子的容量的数组
for(int i=0;i<n;i++) {
num[i] = sc.nextInt();
}
sc.close();
Arrays.sort(num);//给num排一下序
int N = num[n-1]*num[n-1];//dp数组的最大容量
int dp[] = new int[N];//定义dp
dp[0]=1;//初始化dp[0]=1
//求num里面数字的最大公因数
BigInteger g = BigInteger.valueOf(num[0]);
for(int i=0;i<n;i++) {
BigInteger t = BigInteger.valueOf(num[i]);
g = g.gcd(t);
}
if(g.intValue()>1) {
System.out.println("INF");
}else {//状态转移方程:dp[i]=max(dp[i],dp[i-num[j])
for(int i=0;i<N;i++) {
for(int j=0;j<n;j++) {
if(num[j]>i) {
break;
}
dp[i]=Math.max(dp[i], dp[i-num[j]]);
}
}
int sum = Arrays.stream(dp).sum();
System.out.println(N-sum);
}
}
}
到了这里,关于包子凑数【动态规划;数学】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!