DFS
排列数字
#include<iostream>
using namespace std;
int n ;
int a[10];
bool s[10];
void dfs(int u)
{
if(u == n)
{
for(int i = 0 ; i <n ; i++) cout << a[i] << " " ;
cout << endl ;
return;
}
for(int i = 1; i <= n ; i++)
{
if(!s[i])
{
a[u] = i;
s[i] = true ;
dfs(u+1);
a[u] = 0 ;
s[i] = false;
}
}
}
int main()
{
cin >> n ;
dfs(0);
return 0;
}
n皇后
#include<iostream>
using namespace std;
const int N = 20 ;
char g[N][N] ;
bool c[N], x[N] , y[N];
int n , m ;
void dfs(int u)
{
if(u == n)
{
for(int i = 0 ; i < n; i++) cout << g[i] << endl;
cout << endl;
return ;
}
for(int i = 0 ; i < n ; i++)
{
if(!c[i] && !x[u+i] && !y[u-i+n])
{
c[i] = x[u+i] = y[u-i+n] = true ;
g[u][i] = 'Q';
dfs(u+1);
g[u][i] = '.';
c[i] = x[u+i] = y[u-i+n] = false ;
}
}
}
int main()
{
cin >> n;
for(int i = 0 ; i < n ; i++)
for(int j = 0 ; j < n ; j++)
g[i][j] = '.' ;
dfs(0);
return 0 ;
}
BFS
走迷宫
#include<iostream>
#include<cstring>
using namespace std;
typedef pair<int,int> PII ;
const int N = 110 ;
PII q[N * N];
int f[N][N] , d[N][N];
int n , m ;
int dx[] = {0,1,0,-1} , dy[] = {1,0,-1,0} ;
int bfs()
{
memset(d , -1 , sizeof d);
d[1][1] = 0 ;
q[0] = {1,1};
int hh = 0 , tt = 0 ;
while(hh <= tt)
{
auto t = q[hh++] ;
for(int i = 0 ; i < 4 ; i++)
{
int x = t.first + dx[i] , y = t.second + dy[i] ;
if(x<=n &&x>0 && y<=m && y>0 && d[x][y] == -1 && f[x][y] == 0)
{
q[++tt] = {x,y};
d[x][y] = d[t.first][t.second] + 1 ;
}
}
}
return d[n][m];
}
int main()
{
cin >> n >> m ;
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
cin >> f[i][j];
cout << bfs();
return 0;
}
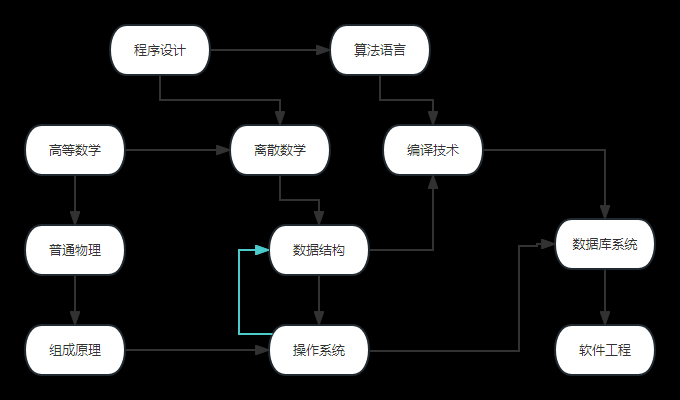
拓扑序列
单链表
点击跳转至例题

idx存的是指针
树与图的深度优先搜索
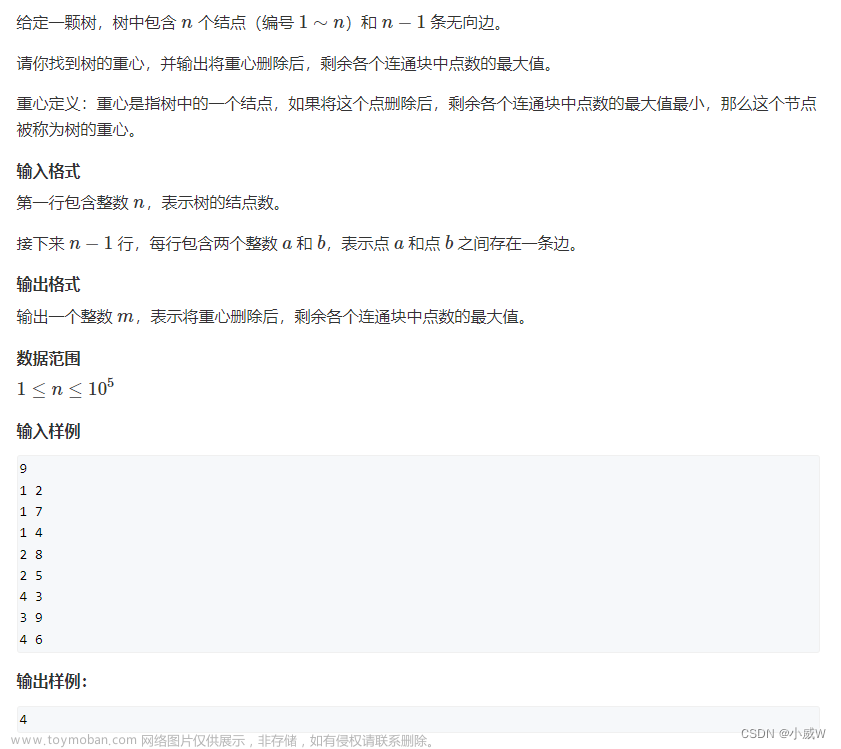
树的重心
每个节点都是一个单链表
模拟队列
hh = 0 , tt = -1文章来源:https://www.toymoban.com/news/detail-478062.html
有向图的拓扑序列

都是从前指向后,即有向无环图(不能有环)
所有入度为0的点,都能排在前面的位置
删掉t->j的边,仅仅是j的入度减一,当j的入度为0的时候,放入队列文章来源地址https://www.toymoban.com/news/detail-478062.html
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e5 + 10;
int n , m ;
int e[N] , h[N] , ne[N] , idx;
int d[N] , q[N];
void add(int a , int b)
{
e[idx] = b , ne[idx] = h[a] , h[a] = idx++;
}
bool topool()
{
int hh = 0 , tt = -1 ;
for(int i = 1; i <= n ; i++)
if(!d[i]) q[++tt] = i ;
while(hh <= tt)
{
int t = q[hh++];
for(int i = h[t] ; i != -1 ; i = ne[i])
{
int j = e[i];
d[j] -- ;
if(d[j] == 0) q[++tt] = j ;
}
}
return tt == n - 1;
}
int main()
{
cin >> n >> m ;
memset(h , -1 , sizeof h) ;
for(int i = 0 ; i < m ; i++)
{
int x,y;
cin >> x >> y;
add(x,y);
d[y]++;
}
if(topool())
{
for(int i = 0 ; i < n ; i++) cout << q[i] << " " ;
}
else cout << -1 ;
return 0;
}
bellman-ford
有边数限制的最短路
spfa
spfa求最短路
spfa判断负环
Floyd
Floyd求最短路
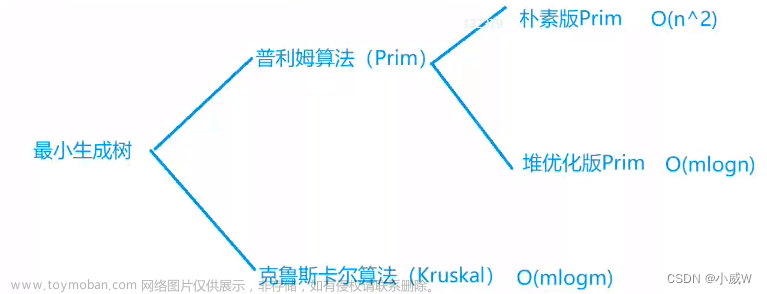
Prim
Prim算法求最小生成树
Kruskal
Kruskal算法求最小生成树
染色法判定二分图
染色法判定二分图
到了这里,关于搜索与图论(acwing算法基础)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!