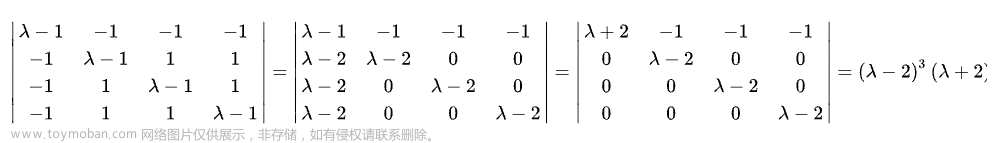行列式基本性质
一、行列式求值

说明:第 i 行元素 乘 第 j 列的代数余子式 之和 = 0
二、转置行列式值不变

引申:行有什么性质,列就有什么性质
三、两行互换,行列式值变号
 引申:两行相同,行列式值为0
引申:两行相同,行列式值为0
四、某行全0 || 两行成比例,行列式=0

五、行列式可拆

注:不要理解错了,二 三行照抄,拆第一行(本着好算的原则拆)
六、行列倍加,值不变

这条性质用的最多
- 加出公因数,提出公因数
- 加出0
重要公式
1.

这里“-1”的次数是:n*(n-1)/2
2.拉普拉斯
3.范德蒙
4.行列式乘法公式
例题
1.利用行列式性质计算
思路:通过初等变换使行列式中先出现1,然后用1使行列式中出现0,再用展开公式。

答案
2.利用拉普拉斯公式

答案
进阶

答案
3.利用范德蒙公式

答案
4.求特征值

观察除主对角线以外的元素,两个数加加减减可以得零,的同时,能够出现λ的公因式。
答案
例题
5.有规律行列式—例题

答案法一:
下面每一行都加到第一行,然后提取公因式。然后消零。出现上三角,直接写出答案。
加出公因式来,提出去,再消零。
答案法二:
下面每一行都减去第一行,做出相反数(x和-x),然后就出现下三角。
答案法三:
第三行的-1倍加到第四行,第二行的-1倍加到第三行,第一行的-1倍加到第二行,出相反数,消出零之后,对第一行展开,出下三角。
总结:
行列式有规律:想办法做公因数,相反数,想办法做0。
行列式无规律:消0,降阶。
6.证明题:证明范德蒙公式

解:
假设n = n-1的时候命题正确。
要证n = n的时候命题正确。
所以想到把n = n时的行列式降阶,因为n-1的行列式是正确的,现在要证明n阶,就要利用n-1阶的信息。
所以要用消零的方法来使n阶行列式降阶。
现在的问题是怎样把n阶行列式降阶。
把n-1行的-x1倍加到第n行,n-2行到第1行以此类推,这样就能把第一列消0。
然后按照第一列展开。
证明完毕!
克拉默法则(多数情况用于证明题)

说明:其中Di 就是把第i列换成常数项的行列式的值。文章来源:https://www.toymoban.com/news/detail-478312.html
推论:
推论二是证 行列式 = 0 的重要构思。文章来源地址https://www.toymoban.com/news/detail-478312.html
到了这里,关于李永乐(一)行列式计算——笔记的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!