1.概念
(1)生成树:如果在一个无向连通图不包含回路(连通图中不存在环),则为一个树
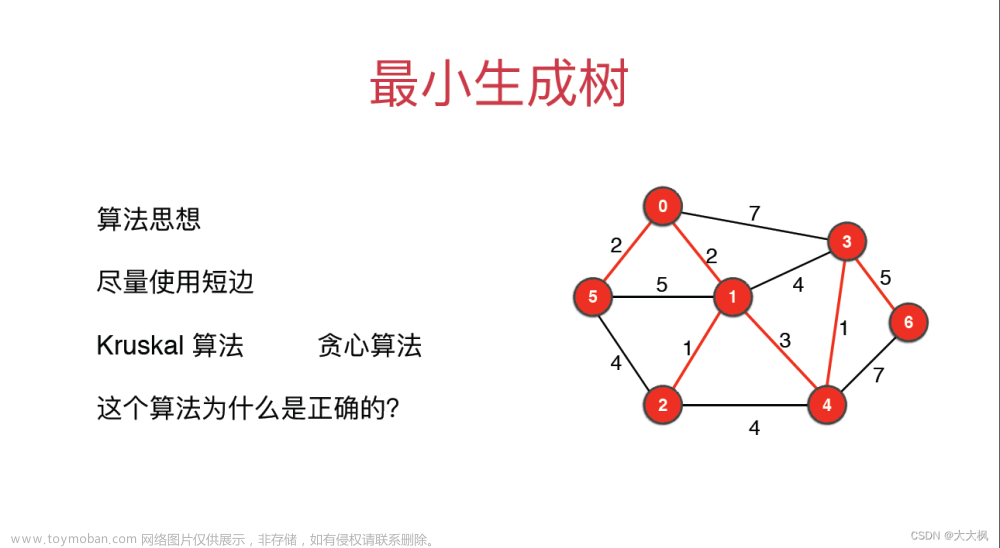
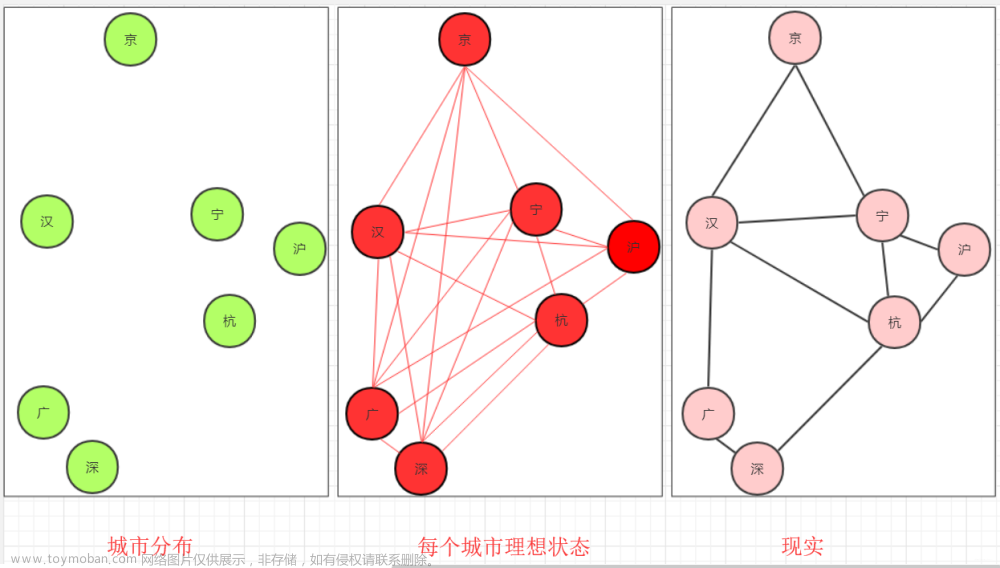
(2)最小生成树(minimal spanning tree):在一个图所有生成树中,代价最小的生成树称为最小生成树
(3)生成树的代价:在一个无向连通网中,生成树各边的权值之和称为该生成树的代价
如何处理点集,使得最小权值的边构成生成树?
1)从一个点出发,依次加入点形成点集(Prim)
2)从边出发,将点集合并,避免形成环(Kruskal)
2.Prim算法
1.思路
将所有顶点分成两个集合,一个是已经加入最小生成树的集合U,一个未加入的集合的V-U,基本过程可以如下描述:(下图来自懒猫老师的《数据结构》相关课程笔记)
(1)先选定一个开始构建最小生成树的结点编号,将选定的结点加入U,其他结点在V-U中

(2) 寻找和该顶点连接的边的最小权值的结点,加入U中

(3) 寻找U中所有结点连接的最小权值的边的结点,(如果有两个结点都和该结点相连,选取权值最小的一条,舍去另一条),并将其加入U中,重复进行,直至所有结点都加入U中

(4)所有结点加入U中,结束

2.数据结构
(1)图的存储:为便于读取任意两顶点之间的权值,采用邻接矩阵存储
(2)shortEdge[n]候选最短边集,包含adjvex和lowcost两个域,分别表示候选最短边的邻接点和权值(lowcost==0代表加入U中)
(3)用prim算法起始点初始化shortEdge[n]数组,后续添加结点过程中,与邻接矩阵中的值比较,再进行修改

3.代码实现
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <limits.h>
#define MAX_VERTEX 10//最大的顶点个数
typedef int DataType;
//无向图
typedef struct PrimNode {
int adjvex;//某一点的前序点
int lowcost;//若该顶点已经属于最小生成树集合U中则赋值0;
//否则值为最小生成树集合U到该点的最小距离(权值);
} PrimNode;
void MGraph(DataType *vertex, int arc[][MAX_VERTEX], int vertexNum, int arcNum) { //初始化构造图(邻接矩阵法)
printf("请逐个输入顶点的内容:");
DataType x;
DataType vi, vj, ave; //构建邻接矩阵时,一条边的两个结点编号
for (int i = 0; i < vertexNum; i++) { //顶点数组赋值
scanf("%d", &x);
vertex[i] = x;
}
for (int i = 0; i < vertexNum; i++) //初始化邻接矩阵
for (int j = 0; j < vertexNum; j++)
arc[i][j] = INT_MAX;//赋值正无穷
int count = 1;
for (int i = 0; i < arcNum; i++) { //依次输入每一条边
printf("请输入第%d条边依附的两个顶点的编号和权值:", count++);
scanf("%d %d %d", &vi, &vj, &ave); //输入该边依附的顶点的编号
arc[vi][vj] = ave; //赋值权值
arc[vj][vi] = ave;
}
}
void Prim(int arc[][MAX_VERTEX], int vertexNum, int start, PrimNode *shortEdge) {
int k;
for (int i = 0; i < vertexNum; i++) {//利用初始结点,初始化辅助数组shortEdge
shortEdge[i].lowcost = arc[start][i];
shortEdge[i].adjvex = start;
}
shortEdge[start].lowcost = 0; //代表该点已经属于最小生成树集合U了
for (int i = 0; i < vertexNum - 1; i++) {//循环找
k = minEdge(shortEdge, vertexNum); //寻找最短边的邻接点k
outputSMT(k, shortEdge, vertexNum); //输出最小生成树路径
shortEdge[k].lowcost = 0; //将顶点k加入到集合U中
for (int j = 0; j < vertexNum; j++) { //调整数组shortEdge[n]
if (arc[k][j] < shortEdge[j].lowcost) {
shortEdge[j].lowcost = arc[k][j];
shortEdge[j].adjvex = k; //标明来自哪个邻接点
}
}
}
}
void outputSMT(int k, PrimNode *shortEdge) {
printf("(%d,%d)%d\n", shortEdge[k].adjvex, k, shortEdge[k].lowcost);
}
int minEdge(PrimNode *shortEdge, int vertexNum) {
int min, flag = 0, index;
for (int i = 0; i < vertexNum; i++) {
if (shortEdge[i].lowcost != 0) {
if (flag == 0) {
min = shortEdge[i].lowcost;
index = i;
flag = 1;
} else if (min > shortEdge[i].lowcost) {
min = shortEdge[i].lowcost;
index = i;
}
}
}
return index;
}
void printMGraph(DataType *vertex, int arc[][MAX_VERTEX], int vertexNum) { //输出
printf("vertex:");
for (int i = 0; i < vertexNum; i++) {
printf("%d ", vertex[i]);
}
printf("\n");
printf("arc:\n");
for (int i = 0; i < vertexNum; i++) {
for (int j = 0; j < vertexNum; j++) {
if (j == vertexNum - 1) {
if (arc[i][j] == INT_MAX)
printf(" *\n");
else
printf(" %d\n", arc[i][j]);
} else {
if (arc[i][j] == INT_MAX)
printf(" * ");
else
printf(" %d ", arc[i][j]);
}
}
}
}
main() {
DataType vertex[MAX_VERTEX];//储存所有的顶点
int arc[MAX_VERTEX][MAX_VERTEX];//邻接矩阵,结点间的连通关系
int vertexNum, arcNum; //顶点个数,边的个数
printf("请输入顶点个数和边的个数:");
scanf("%d %d", &vertexNum, &arcNum);
MGraph(vertex, arc, vertexNum, arcNum);
printf("输出邻接矩阵信息:\n");
printMGraph(vertex, arc, vertexNum);
int x;
printf("请输入Prim算法的起点:");
scanf("%d", &x);
PrimNode shortEdge[vertexNum];
printf("输出起点从编号%d开始的最小生成树:\n", x);
Prim(arc, vertexNum, x, shortEdge);
}4.输出测试

2.Kruskal算法
1.思路
每次选出一条最短边,如果它和当前最小生成树不构成回路就将其加入最小生成树,否则将其删除,直到所有边都处理完毕,基本过程可以如下描述:
(1)将所有的边按照权值从小到大排序,并将所有的结点都看作一棵树,这里要重新定义图的存储
(2)依次将边从小到大加入生成树中

(3)若新加入的边会使已有树生成回路,则舍去

2.数据结构
(1)图的存储:Kruskal算法要求要从小到大的访问边的权值,邻接矩阵和邻接表都显得较麻烦,则需要定义一种新的储存结构,如下:
#define MAX_VERTEX 10//最多顶点个数
#define MAX_EDGE 100//最多边个数
typedef struct EdgeType {
int from, to; //边依附的两个顶点
int weight;//边上的权值
} EdgeType;
struct EdgeGraph {
DataType vertex[MAX_VERTEX];//存放图顶点的数据
EdgeType edge[MAX_EDGE];//存放边的数组
int vertexNum, edgeNum; //图的顶点数和边数
};(2)parent[n]储存所有结点的双亲,若parent[i]==-1,代表该结点为根结点;若一个边相连的两个结点的parent数组的值相同,则代表连接这两个点会形成环,否则就可以合并加入生成树中,同时重新给parent数组赋值
3.代码实现
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define MAX_VERTEX 10//最多顶点个数
#define MAX_EDGE 100//最多边个数
typedef int DataType;
typedef struct EdgeType {
int from, to; //边依附的两个顶点
int weight;//边上的权值
} EdgeType;
struct EdgeGraph {
DataType vertex[MAX_VERTEX];//存放图顶点的数据
EdgeType edge[MAX_EDGE];//存放边的数组
int vertexNum, edgeNum; //图的顶点数和边数
};
main() {
int vertexNum, arcNum; //顶点个数,边的个数
printf("请输入顶点个数和边的个数:");
scanf("%d %d", &vertexNum, &arcNum);
struct EdgeGraph graph;
Graph(&graph, vertexNum, arcNum);
ranklist(&graph);
printf("输出通过边信息储存的图:\n");
printGraph(graph);
int parent[vertexNum];//每一个结点的双亲结点(根结点)
printf("输出Kruskal算法得的最小生成树(from,to)weght:\n");
Kruskal(graph, parent);
}
void Graph(struct EdgeGraph *graph, int vertexNum, int arcNum) {
graph->edgeNum = arcNum;
graph->vertexNum = vertexNum;
printf("请逐个输入顶点的内容:");
DataType x;
for (int i = 0; i < vertexNum; i++) { //顶点数组赋值
scanf("%d", &x);
graph->vertex[i] = x;
}
int count = 1;
int a, b, ave;
for (int i = 0; i < arcNum; i++) { //依次输入每一条边
printf("请输入第%d条边依附的两个顶点的编号和权值:", count++);
scanf("%d %d %d", &a, &b, &ave); //输入该边依附的顶点的编号
graph->edge[i].from = a;
graph->edge[i].to = b;
graph->edge[i].weight = ave;
}
}
void ranklist(struct EdgeGraph *graph) { //将图的边数组按边的权值从小到大排序
EdgeType temp;
for (int i = 0; i < graph->edgeNum ; i++) { //冒泡排序
for (int j = 0; j < graph->edgeNum - i - 1; j++) {
if (graph->edge[j].weight > graph->edge[j + 1].weight) {
temp = graph->edge[j];
graph->edge[j] = graph->edge[j + 1];
graph->edge[j + 1] = temp;
}
}
}
}
void Kruskal(struct EdgeGraph graph, int *parent) {
for (int i = 0; i < graph.vertexNum; i++)
parent[i] = -1; //初始化双亲数组,值为-1代表本身为根结点
int num, i, vex1, vex2;
for (num = 0, i = 0; i < graph.edgeNum; i++) {
vex1 = findRoot(parent, graph.edge[i].from); //找到所在生成树的根结点
vex2 = findRoot(parent, graph.edge[i].to); //找到所在生成树的根结点
if (vex1 != vex2) { //找到的两个根结点不同,不会构成环
outputMST(graph.edge[i]);//输出加入的边
parent[vex2] = vex1; //合成生成树
num++;
if (num == graph.vertexNum - 1) //循环了“图的顶点数-1”次,提前返回
return;
}
}
}
int findRoot(int *parent, int v) {
int t = v;
while (parent[t] > -1)
t = parent[t]; //求顶点t上的双亲直达根结点
return t;
}
void outputMST(EdgeType x) {
printf("(%d,%d)%d\n", x.from, x.to, x.weight);
}
void printGraph(struct EdgeGraph graph) {
printf(" no from to weight\n");
for (int i = 0; i < graph.edgeNum; i++) {
printf(" edge[%d] %d %d %d\n", i, graph.edge[i].from, graph.edge[i].to, graph.edge[i].weight);
}
}4.输出测试
 文章来源:https://www.toymoban.com/news/detail-478600.html
文章来源:https://www.toymoban.com/news/detail-478600.html
初学小白,有错误的话欢迎指正!文章来源地址https://www.toymoban.com/news/detail-478600.html
到了这里,关于最小生成树(Prim算法,Kruskal算法)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!