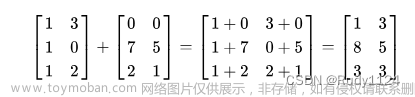
矩阵乘法
| 0 | 1 |
|---|---|
| 1 | 1 |
这是一个矩阵,那么我要让它乘以一个这样的矩阵
| 1 | 0 |
|---|---|
| 0 | 1 |
那么它的结果就是
| 0 | 1 |
|---|---|
| 1 | 1 |
如果乘以它自身,那么它的结果就是
| 1 | 1 |
|---|---|
| 1 | 2 |
那么矩阵乘法的公式就应该是
(此图为网图,侵权可以私信我)
可以发现,矩阵乘法的右单位元应该是
| 1 | 0 | 0 |
|---|---|---|
| 0 | 1 | 0 |
| 0 | 0 | 1 |
后面的以此类推
因为对于当前行的每一列都会都会乘以一个对应的数,那么当前列要保留的数所对应的位置就应该是 \(1\),那么经过猜测推算就可以得出上述矩阵。
另外矩阵乘法满足结合律,证明我也不会 (T﹏T)。
矩阵乘法优化递推
斐波那契数列
斐波那契数列你显然可以用 \(O(n)\) 的时间求出来,递推即可。
但是如果 \(n\) 为 \(1e18\) 你就炸开了,所以需要一种方法优化线性的时间复杂度。
由于 \(f_i = f_{i - 1} + f_{i - 2}\) 那么可以变成从 \([f_{i - 2}, f_{i - 1}]\) 到 \([f_{i - 1}, f_{i}]\) 的这样一个过程,我们发现这个其实是个矩阵,其中 \(i\) 是要求和的,而其它的不要保留第一个即可,那么可以由上面讲的矩阵乘法的右单位元和斐波那契数列的递推公式来推出斐波那契数列的这个变化用的矩阵应该是
| 0 | 1 |
|---|---|
| 1 | 1 |
由于下面还要用,所以将该矩阵设为 \(x\)。
所以我们就可以知道 \(f_i\) 怎么求了,那么可以得出任何数的求法,可是还是 \(O(n)\) 的,我们看看式子就明白了怎么做:
\([f_i, f_{i + 1}] = ((([f_1, f_2] \times x) \times x) \times \dots \dots ) \times x\)
由于满足结合律可以拆括号为
\([f_i, f_{i + 1}] = [f_1, f_2] \times x \times x \times \dots \dots \times x\)
还能简化为
\([f_i, f_{i + 1}] = [f_1, f_2] \times x^i\)
那么就很好算了呀,代码如下
#include <algorithm>
#include <iostream>
using namespace std;
using ll = long long;
const int MaxN = 110, mod = 1e9 + 7;
struct A {
int n, m;
ll a[MaxN][MaxN];
A() {
fill(a[1], a[MaxN], 0);
}
void build() {
for (int i = 1; i < MaxN; i++) {
a[i][i] = 1;
}
}
void init() {
for (int i = 1; i < m; i++) {
a[i + 1][i] = 1;
}
for (int i = 1; i <= n; i++) {
a[i][m] = 1;
}
}
A operator*(const A &b) const {
A c;
c.n = n, c.m = b.m;
for (int i = 1; i <= n; i++) {
for (int k = 1; k <= m; k++) {
for (int j = 1; j <= b.m; j++) {
c.a[i][j] = (c.a[i][j] + a[i][k] * b.a[k][j] % mod) % mod;
}
}
}
return c;
}
} a, c;
ll n, m = 2;
A qpow(A a, ll b) {
A res;
res.build(), res.n = a.n, res.m = a.m;
for (ll i = 1; i <= b; i <<= 1) {
if (b & i) {
res = res * a;
}
a = a * a;
}
return res;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
a.n = 1, a.m = m;
a.a[a.n][a.m] = 1;
c.n = c.m = m, c.init();
c = qpow(c, n), a = a * c;
cout << a.a[1][m] << '\n';
return 0;
}
那么如果是 \(f_i = f_{i - 1} + f_{i - 2} + \dots \dots + f_{i - m}\) 呢
那么我们其实可以理解为斐波那契数列的扩展,那么同样的我们可以得到变化是要乘的矩阵应该是,对于每个 \(i\) 其 \([i + 1, i]\) 为一,且第 \(m\) 列全为 \(1\)。
代码如下
#include <algorithm>
#include <iostream>
using namespace std;
using ll = long long;
const int MaxN = 110, mod = 1e9 + 7;
struct A {
int n, m;
ll a[MaxN][MaxN];
A() {
fill(a[1], a[MaxN], 0);
}
void build() {
for (int i = 1; i < MaxN; i++) {
a[i][i] = 1;
}
}
void init() {
for (int i = 1; i < m; i++) {
a[i + 1][i] = 1;
}
for (int i = 1; i <= n; i++) {
a[i][m] = 1;
}
}
A operator*(const A &b) const {
A c;
c.n = n, c.m = b.m;
for (int i = 1; i <= n; i++) {
for (int k = 1; k <= m; k++) {
for (int j = 1; j <= b.m; j++) {
c.a[i][j] = (c.a[i][j] + a[i][k] * b.a[k][j] % mod) % mod;
}
}
}
return c;
}
} a, c;
ll n, m;
A qpow(A a, ll b) {
A res;
res.build(), res.n = a.n, res.m = a.m;
for (ll i = 1; i <= b; i <<= 1) {
if (b & i) {
res = res * a;
}
a = a * a;
}
return res;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
a.n = 1, a.m = m;
a.a[a.n][a.m] = 1;
c.n = c.m = m, c.init();
c = qpow(c, n), a = a * c;
cout << a.a[1][m] << '\n';
return 0;
}
P2106 Sam数
思路
首先考虑暴力求解,我们设 \(dp_{ij}\) 表示,考虑到第 \(i\) 位,而当前位为 \(j\),那么对于这种状态,我们很快就能想到一种转移:
\(dp_{ij}=\sum\limits_{k=j-2}^{j+2}dp_{i-1k}\)文章来源:https://www.toymoban.com/news/detail-478618.html
然后我们会发现这样子不管是时间还是空间,都是会爆的,因为这题线性都不行,那么我们就需要矩阵乘法优化,我们发现一点,\(i\) 层的答案将会是所有可能性的和,那么我们可以设计矩形状态为 \(f_{i0}~f_{i9}\)表示 \(i\) 层,的所有可能状态,然后问么就可以推测出单位矩正为多少,然后快速幂计算即可文章来源地址https://www.toymoban.com/news/detail-478618.html
code
#include <algorithm>
#include <iostream>
using namespace std;
using ll = long long;
const int MaxN = 20, mod = 1000000007;
struct A {
int n, m;
ll a[MaxN][MaxN];
A() {
fill(a[0], a[MaxN], 0);
}
void build() {
for (int i = 0; i < MaxN; i++) {
a[i][i] = 1;
}
}
void init() {
for (int i = 0; i <= n; i++) {
for (int j = max(i - 2, 0); j <= min(i + 2, m); j++) {
a[i][j] = 1;
}
}
}
A operator*(const A &b) const {
A c;
c.n = n, c.m = b.m;
for (int i = 0; i <= n; i++) {
for (int k = 0; k <= m; k++) {
for (int j = 0; j <= b.m; j++) {
c.a[i][j] = (c.a[i][j] + a[i][k] * b.a[k][j] % mod) % mod;
}
}
}
return c;
}
} a, c;
ll n, m = 9, ans;
A qpow(A a, ll b) {
A res;
res.build(), res.n = a.n, res.m = a.m;
for (ll i = 1; i <= b; i <<= 1) {
if (b & i) {
res = res * a;
}
a = a * a;
}
return res;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
a.n = 0, a.m = m;
for (int i = 0; i <= m; i++) {
a.a[0][i] = 1;
}
c.n = c.m = m, c.init();
c = qpow(c, n - 1), a = a * c;
for (int i = 1; i <= m; i++) {
ans = (ans + a.a[0][i]) % mod;
}
cout << ans + (n == 1) << endl; // 如果位数是1的话那么前导0不是前导了
return 0;
}
到了这里,关于矩阵乘法与优化的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!