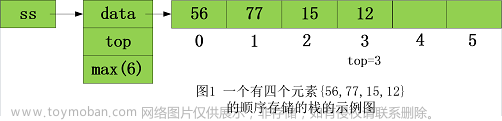
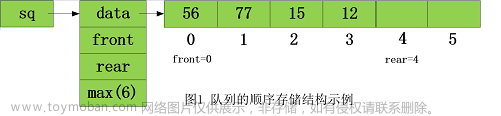
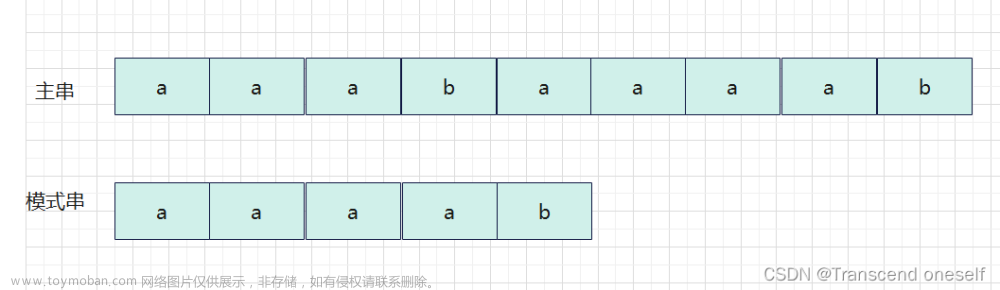
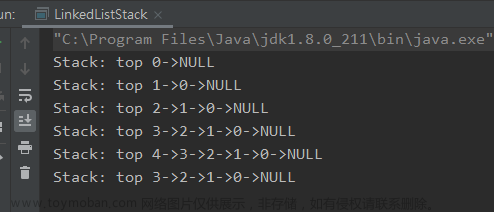
前言
当我们编写程序时,经常需要处理各种数据结构。队列是一种常见的数据结构,它有着广泛的应用场景。队列的基本操作包括入队和出队,应用于模拟等待队列、消息队列、计算机缓存等场合。
在实际编程中,我们可以用不同的数据结构来实现队列。本文主要介绍了三种不同的队列实现方式,包括带头结点单向队列、不带头结点单向队列和循环队列。这些队列实现方式分别使用了链表、数组等不同的数据结构,在实现细节、时间复杂度和空间利用率等方面具有不同的特点。对于程序员来说,了解不同的队列实现方式,可以更好地选择适合自己应用场景的队列实现方式,提高程序的效率。
队列实现
队列是一种先进先出(First-In-First-Out, FIFO)的数据结构,它的基本操作包括入队(将元素插入队尾)和出队(将队首元素删除)。
带头结点单向队列
-
带头结点单向队列是一种使用链表实现的队列,与普通链表不同的是,带头结点单向队列在链表头部添加一个不存储数据的节点,作为链表的头结点,用于方便队列的操作。
-
在带头结点单向队列中,入队操作是将新元素插入到链表尾部,出队操作是将队首元素的后继节点作为新的队首节点。
-
由于链表的特性,带头结点单向队列的入队操作是 O ( 1 ) O(1) O(1) 的,而出队操作需要遍历整个链表,因此其时间复杂度为 O ( n ) O(n) O(n),其中 n n n 表示队列的元素个数。
下面展示一张图表示队列插入的逻辑:
队列节点结构体设计:
// 节点结构体
struct queueNode
{
// 数据元素
int elem;
// 指向下一个元素
struct queueNode *next;
};
struct queue
{
// 尾部
struct queueNode *rear;
// 头部
struct queueNode *front;
// 长度
int lenth;
};
代码实现:
/********************** 含头结点 ***************/
// 队列初始化
struct queue*queueInit()
{
// 申请空间并且初始化
struct queue*res = (struct queue*)malloc(sizeof(struct queue));
// 初始化一个虚拟节点
struct queueNode*node = (struct queueNode*)malloc(sizeof(struct queueNode));
res->front = node;
res->rear = node;
res->lenth = 0;
return res;
}
// 入队列
void pushQueueNode(struct queue*queue, int elem)
{
// 新建一个节点
struct queueNode*node = (struct queueNode*)malloc(sizeof(struct queueNode));
node->elem = elem;
node->next = NULL;
// 添加到尾部
queue->rear->next = node;
queue->rear = node;
queue->lenth++;
}
// 出队列
bool pullQueueNode(struct queue*queue, int&elem)
{
// 判断队列是否为空
if (queueIsEmpty(queue))
return true;
// 移除队列中的首元素
struct queueNode*p = queue->front->next;
elem = p->elem;
queue->front->next = p->next;
queue->lenth--;
// 队列中只有一个元素应该改变队尾指针
if (queue->rear == p)
queue->rear = queue->front;
free(p);
return false;
}
// 判断队列是否空
bool queueIsEmpty(struct queue*queue)
{
return queue->lenth == 0;
}
// 打印队列
void outPutQueue(struct queue*queue)
{
// 判断队列是否为空
if (queue->lenth == 0)
return;
struct queueNode*p = queue->front->next;
// 遍历队列并打印
printf("queue:");
while (p)
{
printf("%d ",p->elem);
p = p->next;
}
printf("\n");
}
不带头结点单向队列
-
与带头结点单向队列相比,不带头结点单向队列不使用头结点,直接从链表的第一个节点开始存储数据。
-
在不带头结点单向队列中,入队操作是将新元素插入到链表尾部,出队操作是删除链表的头结点,并将头结点的后继节点作为新的队首节点。
-
由于每次出队操作都需要删除链表的头结点,因此不带头结点单向队列中的实现会导致频繁的内存分配和释放,效率比较低。
其插入操作的图解为:
队列节点结构体设计:
struct queueNode
{
// 数据元素
int elem;
// 指向下一个元素
struct queueNode *next;
};
代码实现:
/********************** 不含头结点 ***************/
// 队列初始化
struct queue*vQueueInit()
{
// 申请空间并且赋值
struct queue*res = (struct queue*)malloc(sizeof(struct queue));
res->lenth = 0;
res->front = res->rear = NULL;
return res;
}
// 打印队列
void vOutPutQueue(struct queue*queue)
{
printf("queue:");
struct queueNode*p = queue->front;
// 遍历打印
while (p)
{
printf("%d ",p->elem);
p = p->next;
}
printf("\n");
}
// 入队列
void vPushQueueNode(struct queue*queue, int elem)
{
// 申请一个节点
struct queueNode *p = (struct queueNode*)malloc(sizeof(struct queueNode));
p->elem = elem;
p->next = NULL;
// 队列为空时入队列
if (queue->lenth == 0)
{
queue->front = p;
queue->rear = p;
}
else
{
// 先将节点接到队列上
queue->rear->next = p;
// 再移动队列尾指针
queue->rear = p;
}
queue->lenth++;
}
// 出队列
bool vPullQueueNode(struct queue*queue, int&elem)
{
// 判断队列是否为空
if (vQueueIsEmpty(queue))
return false;
// 获取队列首元素 并返回
struct queueNode*p = queue->front;
elem = p->elem;
queue->front = p->next;
queue->lenth--;
return true;
}
// 判断队列是否空
bool vQueueIsEmpty(struct queue*queue)
{
return queue->lenth == 0;
}
与含头结点队列操作上的区别:主要在于入队列与出队列时需要判断队列是否为空。
循环队列
-
循环队列是一种使用数组实现的队列,与普通数组不同的是,循环队列的队尾指针和队首指针可以在达到数组的末尾位置时循环到数组的开头位置。
-
在循环队列中,需要使用两个指针分别指向队首和队尾,或者使用一个指针和队列长度维护队首和队尾位置。
-
在循环队列中,入队操作是将新元素插入到队尾,如果队列满了,则会返回队列已满的错误;出队操作是将队首元素删除,并将队首指针指向下一个元素。
-
循环队列的主要优点是空间利用率比较高,可以实现环形存储,而且操作的时间复杂度比带头结点单向队列和不带头结点单向队列都要高效,都是 O ( 1 ) O(1) O(1)。
队列结构体设计:
// 队列的最大长度
#define QUEUEMAXSIZE 10
// 队列结构体
struct queueCirculate
{
// 存储数据
int data[QUEUEMAXSIZE];
// 记录数量
int count;
// 记录队列队头
int front;
// 记录队列队尾
int rear;
};
队列节点结构体设计:
******************** 循环队列 ******************/
// 初始化循环队列
struct queueCirculate*queueCirculateInit(void)
{
// 申请空间
struct queueCirculate*res = (struct queueCirculate*)malloc(sizeof(struct queueCirculate));
// 初始化队列的数量 队头队尾的位置
res->count = 0;
res->front = 0;
res->rear = 0;
return res;
}
// 入队列
bool pushQueueCirculate(struct queueCirculate*queue,int elem)
{
// 判断队列是否已满
if (queue->count == QUEUEMAXSIZE)
return false;
// 入队列
queue->data[queue->rear] = elem;
// 改变队尾指针的位置 以及 队列的数量
queue->count++;
if (queue->count < QUEUEMAXSIZE)
queue->rear = (queue->rear + 1) % QUEUEMAXSIZE;
return true;
}
// 出队列
bool pullQueueCirculate(struct queueCirculate*queue, int&elem)
{
// 判断队列是否为空
if (queue->count == 0)
return false;
// 出队列
elem = queue->data[queue->front];
// 移动队头指针 并且 改变队列元素数量
queue->front = (queue->front + 1) % QUEUEMAXSIZE;
queue->count--;
return true;
}
// 队列是否为空
bool queueCirculateIsEmpty(struct queueCirculate*queue)
{
return queue->count == 0;
}
// 打印队列
void outPutQueueCirculate(struct queueCirculate*queue)
{
int count = queue->count;
printf("queue: ");
for (int i = 0; i < count; ++i)
{
int temp = -1;
pullQueueCirculate(queue, temp);
printf("%d ", temp);
}
printf("\n");
}
总结
带头结点单向队列、不带头结点单向队列和循环队列各有优缺点,适用于不同的应用场景:
带头结点单向队列适用于需要实现入队操作频繁、出队操作较少的场景。它可以利用链表的特性,实现入队操作的时间复杂度为 O(1),缺点是出队操作的时间复杂度为 O(n)。
不带头结点单向队列适用于队列长度较短的需要入队和出队操作都比较频繁的场景。由于不使用头结点,可以节省一些空间,但出队操作需要频繁的内存分配和释放,效率比较低。
循环队列适用于队列长度较大且入队和出队操作都比较频繁的场景。它的环形存储结构可以充分利用数组的连续存储空间,实现了空间的高效利用。同时,入队和出队操作的时间复杂度都为 O(1),效率比较高。但是,循环队列需要事先定义一个最大长度,如果队列长度超过了最大长度,需要进行扩容操作。此外,由于环形结构的特殊性,实现起来也比较复杂。文章来源:https://www.toymoban.com/news/detail-478720.html
因此,在选择队列实现方式时,需要根据具体的应用场景综合考虑时间复杂度、空间利用率和实现难度等因素,选择最适合自己的队列实现方式。文章来源地址https://www.toymoban.com/news/detail-478720.html
到了这里,关于【数据结构与算法分析】使用C语言实现队列的两种(带头结点与不带头结点)链式存储,并且给出一种循环队列的设计思想的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!