【数据结构与算法】03 队列（顺序队列--循环队列--优先级队列--链队列）

一、概念

1.1 队列的基本概念

队列（queue）是一种常见的数据结构，它遵循先进先出（FIFO）的原则。队列可以理解为一个具有两个端点的线性数据结构，其中一个端点称为"队尾"（rear），用于插入新元素，另一个端点称为"队首"（front），用于移除元素。新元素被插入到队尾，而最早插入的元素总是在队首。

队列的特点如下：

• 元素按照插入顺序排列，最先插入的元素在队列中的位置最靠前，即队首。
• 只能从队首移除元素，而只能在队尾插入新元素，遵循先进先出的原则。
• 队列的长度可以动态变化，根据插入和移除操作进行调整。

队列常常用于需要按照先后顺序处理数据的场景，例如任务调度、消息传递、广度优先搜索等。

队列的基本操作包括：

• 入队（Enqueue）：将新元素插入到队尾。
• 出队（Dequeue）：移除队首的元素，并返回该元素。
• 队列是否为空（isEmpty）：判断队列是否为空。
• 队列长度（size）：返回队列中元素的个数。
• 获取队首元素（front）：返回队首元素，但不移除它。

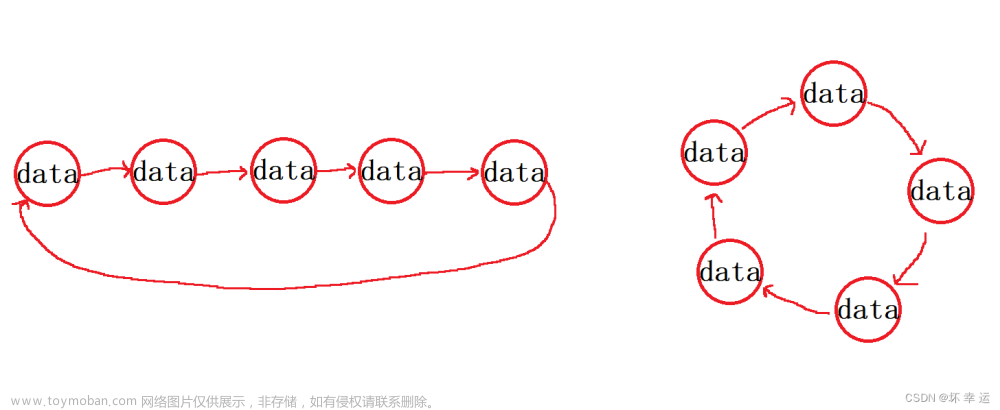
队列可以通过不同的数据结构来实现，常见的实现方式包括使用数组或链表。

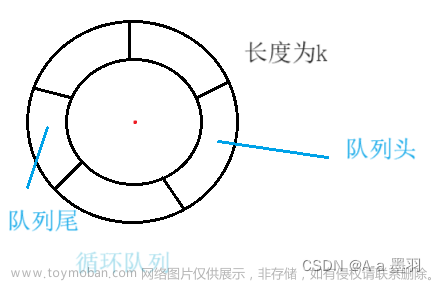
使用数组实现的队列称为顺序队列，而使用链表实现的队列称为链式队列。此外，还有循环队列，它使用数组实现，通过循环利用数组空间来提高效率。

1.2 队列的顺序存储结构

1.21 顺序队列（静态队列）

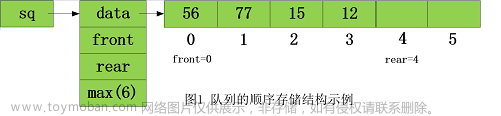
顺序队列是一种使用数组实现的队列（array-based），它是队列的一种常见实现方式。顺序队列的特点是元素按照插入顺序排列，并且只能从队首移除元素，从队尾插入新元素，遵循先进先出（FIFO）的原则。

顺序队列的实现依赖于一个固定大小的数组，通过数组的索引来表示队列的头部和尾部。以下是顺序队列的一些关键操作：（假设队首、队尾索引都初始化为0，这样队首索引=队首元素索引；队尾索引等于队尾元素索引+1。理解意思即可）

1. 入队（Enqueue）：将新元素插入到队尾。当有元素需要入队时，需要将其插入到数组的尾部，并更新队尾的索引。
2. 出队（Dequeue）：移除队首的元素，并返回该元素。出队操作需要将队首元素移除，并更新队首的索引。
3. 队列是否为空（isEmpty）：判断队列是否为空。当队首和队尾的索引相等时，表示队列为空。
4. 队列是否已满（isFull）：判断队列是否已满。当队尾的索引达到数组的最大容量时，表示队列已满，无法插入新元素。
5. 队列长度（size）：返回队列中元素的个数。计算方法是队尾索引减去队首索引。
6. 获取队首元素（front）：返回队首元素，但不移除它。可以直接通过队首索引来访问数组中的元素。
   

• 顺序队列的优点是实现简单、操作高效，入队和出队的时间复杂度均为O(1)。
• 但是顺序队列的缺点是固定大小，当队列已满时无法插入新元素，且需要移动元素位置来保持队列的连续性，导致效率降低。

为了解决空间利用率低的问题，还可以使用循环队列，它使用数组实现，并通过循环利用数组空间来提高效率。循环队列的实现方式使得插入和删除操作都能在常数时间内完成，而不需要移动元素位置。

1.22 循环队列

循环队列（circular queue）是一种基于数组实现的队列数据结构，它解决了普通队列在出队操作后浪费存储空间的问题。循环队列的特点是队尾和队头可以通过取模运算实现循环移动。

循环队列的主要特点和实现细节：

• 使用数组实现：循环队列使用数组作为底层数据结构，通过索引来访问队列中的元素。
• 队首和队尾指针：循环队列使用两个指针来标记队列的头部和尾部。通常使用 front 指针表示队首元素的位置，rear 指针表示队尾元素的位置。
• 空队列判断：当 front 和 rear 指针指向同一个位置时，队列为空（也可以用一个变量实时记录队列元素个数，方便不少）。
• 满队列判断：当 (rear + 1) % capacity = front 时，队列为满（capacity：数组大小）。
• 入队操作：向循环队列中插入元素时，先判断队列是否已满。如果队列未满，将元素插入到 rear 指针指向的位置，并将 rear 指针向后移动一位（rear = (rear + 1) % capacity）。
• 出队操作：从循环队列中删除元素时，先判断队列是否为空。如果队列不为空，将 front 指针向后移动一位（front = (front + 1) % capacity）。
• 遍历队列：可以使用循环遍历队列中的所有元素，从 front 指针开始逐个移动并访问元素，直到 front 指针与 rear 指针相等。
  入队图示：
  

循环队列的优点是能够更有效地利用存储空间，避免了数据迁移的开销。它适用于需要频繁进行入队和出队操作的场景，例如消息队列、任务调度等。

但是，循环队列的容量需要预先确定，并且一旦确定后就不能改变。在实现循环队列时，需要合理处理指针的移动和边界条件，确保队列操作的正确性。

1.23 优先级队列

优先级队列（priority queue）是一种特殊的队列，其中每个元素都关联有一个优先级。元素的优先级决定了其在队列中的位置和顺序。优先级高的元素在队列中排在前面，而优先级低的元素排在后面。

相关概念和操作：

• 元素优先级：每个元素都与一个优先级相关联，可以是数字、字符或其他可比较的类型。较高的优先级对应较高的值。
• 插入操作：将元素插入优先级队列时，根据元素的优先级将其放置在适当的位置。通常，较高优先级的元素被放置在队列的前面，而较低优先级的元素被放置在后面。
• 删除操作：从优先级队列中删除元素时，总是删除具有最高优先级的元素。这通常是队列的第一个元素。
• 更新操作：如果需要更改元素的优先级，可以更新元素在队列中的位置。这通常需要重新排序或调整队列的内部结构。
• 遍历操作：可以按照优先级顺序遍历优先级队列中的所有元素。这样可以按照优先级高低的顺序处理元素。
  例：下图将高优先级的元素放在队首（这里数值越小优先级越高），相同优先级则遵循先进先出规则。
  

优先级队列常用于需要按照某种优先级顺序处理元素的场景。例如，任务调度器可以使用优先级队列来管理待执行的任务，确保高优先级任务优先执行。还可以在模拟系统中使用优先级队列来模拟事件的发生顺序。

在实现优先级队列时，可以使用各种数据结构，如链表、二叉搜索树或有序数组。这些数据结构提供了高效的插入、删除和查找操作，以满足优先级队列的需求。（本文使用数组实现）

在处理具有相同优先级的元素时，可以根据应用程序的需求使用先入先出（FIFO）规则或后入先出（LIFO）规则来确定元素的顺序。这决定了相同优先级的元素在队列中的相对位置。

1.3 队列的链式存储结构

链式队列是一种使用链表实现的队列数据结构。与数组队列相比，链式队列不需要预先指定固定大小，可以动态地添加和删除元素。

主要特点和实现细节：

• 链表结构：链式队列使用链表来存储元素。每个节点包含一个数据元素和一个指向下一个节点的指针。
• 头尾指针：链式队列维护两个指针，分别指向队列的头部和尾部节点。入队操作将新节点链接到尾部节点，并更新尾部指针。出队操作删除头部节点，并更新头部指针。
• 空队列处理：链式队列可以处理空队列的情况，即当队列为空时，出队操作将返回一个特定的值（如NULL）或引发异常。
• 动态大小：由于链式队列使用动态链表存储元素，它可以根据需要动态增长或缩小。这使得链式队列更加灵活，可以适应不同的元素数量和大小需求。
  

链式队列的优点包括灵活性和动态大小，适用于处理变化的元素数量。然而，与数组队列相比，链式队列需要额外的内存来存储节点指针，并且在访问特定位置的元素时需要遍历链表，可能导致一些性能开销。

在实现链式队列时，可以定义一个节点结构来表示链表中的每个节点，并使用指针来跟踪队列的头部和尾部。通过使用指针操作，可以在常量时间内执行入队和出队操作。

在多线程环境中使用链式队列时，需要考虑线程安全性和同步问题，以避免竞态条件和数据不一致的情况。可以使用互斥锁或其他同步机制来确保线程安全性。

二、C语言实现

记得是队尾插入，队首删除。

2.1 顺序存储

2.11 顺序队列

// 顺序队列
#include <stdio.h>

#define MAX_SIZE 100

// 定义队列结构体
typedef struct {
    int data[MAX_SIZE];
    int front;  // 队首索引
    int rear;   // 队尾索引
} Queue;

// 初始化队列
void initQueue(Queue *queue) {
    queue->front = 0;
    queue->rear = 0;
}

// 判断队列是否为空
int isEmpty(Queue *queue) {
    return (queue->front == queue->rear);
}

// 判断队列是否已满
int isFull(Queue *queue) {
    return (queue->rear == MAX_SIZE);
}

// 入队
void enqueue(Queue *queue, int item) {
    if (isFull(queue)) {
        printf("队列已满，无法插入元素\n");
        return;
    }

    queue->data[queue->rear] = item;
    queue->rear++;
}

// 出队
int dequeue(Queue *queue) {
    if (isEmpty(queue)) {
        printf("队列为空，无法删除元素\n");
        return -1;
    }

    int item = queue->data[queue->front];
    queue->front++;

    return item;
}

// 获取队列长度
int getQueueLength(Queue *queue) {
    return queue->rear - queue->front;
}

int main() {
    Queue queue;
    initQueue(&queue);

    enqueue(&queue, 1);
    enqueue(&queue, 2);
    enqueue(&queue, 3);

    printf("队列长度: %d\n", getQueueLength(&queue));

    printf("出队元素: %d\n", dequeue(&queue));
    printf("出队元素: %d\n", dequeue(&queue));

    printf("队列长度: %d\n", getQueueLength(&queue));

    return 0;
}

2.12 循环队列

// 循环队列
#include <stdio.h>

#define MAX_SIZE 100

// 定义循环队列结构体
typedef struct {
    int data[MAX_SIZE];
    int front;  // 队首索引
    int rear;   // 队尾索引
    int size;   // 直接用一个size来记录大小，简化空、满的判断
} CircularQueue;

// 初始化循环队列
void initQueue(CircularQueue *queue) {
    queue->front = 0;
    queue->rear = 0;
    queue->size = 0;
}

// 判断循环队列是否为空
int isEmpty(CircularQueue *queue) {
    return (queue->size == 0);
}

// 判断循环队列是否已满
int isFull(CircularQueue *queue) {
    return (queue->size == MAX_SIZE);
}

// 入队
void enqueue(CircularQueue *queue, int item) {
    if (isFull(queue)) {
        printf("循环队列已满，无法插入元素\n");
        return;
    }

    queue->data[queue->rear] = item;
   // 注意对队尾索引的计算，因为它是循环的 
    queue->rear = (queue->rear + 1) % MAX_SIZE;
    // 更新元素个数
    queue->size++;
}

// 出队
int dequeue(CircularQueue *queue) {
    if (isEmpty(queue)) {
        printf("循环队列为空，无法删除元素\n");
        return -1;
    }

    int item = queue->data[queue->front];
    // 同理
    queue->front = (queue->front + 1) % MAX_SIZE;
    queue->size--;

    return item;
}

// 获取循环队列长度
int getQueueLength(CircularQueue *queue) {
    return queue->size;
}

int main() {
    CircularQueue queue;
    initQueue(&queue);

    enqueue(&queue, 1);
    enqueue(&queue, 2);
    enqueue(&queue, 3);

    printf("循环队列长度: %d\n", getQueueLength(&queue));

    printf("出队元素: %d\n", dequeue(&queue));
    printf("出队元素: %d\n", dequeue(&queue));

    printf("循环队列长度: %d\n", getQueueLength(&queue));

    return 0;
}

2.13 优先级队列

注意，优先级通常是数值越小，优先级越高。计算机领域通常都是这样的。（当然你也可以自定义）

#include <stdio.h>

#define MAX_SIZE 100

typedef struct {
    int value;
    int priority;
} Element;

Element queue[MAX_SIZE];
int size = 0;

void enqueue(int value, int priority) {
    if (size >= MAX_SIZE) {
        printf("Queue is full. Unable to enqueue.\n");
        return;
    }
    
    int i = size - 1;
    while (i >= 0 && queue[i].priority > priority) {
        queue[i + 1] = queue[i];
        i--;
    }
    
    queue[i + 1].value = value;
    queue[i + 1].priority = priority;
    size++;
}

int dequeue() {
    if (size <= 0) {
        printf("Queue is empty. Unable to dequeue.\n");
        return -1; // Return a sentinel value indicating an error
    }
    
    int value = queue[0].value;
    
    for (int i = 1; i < size; i++) {
        queue[i - 1] = queue[i];
    }
    
    size--;
    return value;
}

void traverse() {
    if (size <= 0) {
        printf("Queue is empty. Nothing to traverse.\n");
        return;
    }
    
    printf("Queue traversal: \n\t");
    for (int i = 0; i < size; i++) {
        printf("Val: %3d   Prio: %d\n\t", queue[i].value, queue[i].priority);
    }
    printf("\n");
}

int main() {
    enqueue(5, 3);
    enqueue(10, 1);
    enqueue(3, 6);
    
    traverse();
    
    int value = dequeue();
    printf("Dequeued value: %d\n", value);
    
    traverse();

    enqueue(888, 4);
    printf("Enter (888,4)\n");
    traverse();
    
    return 0;
}

2.2 链式存储

// 链队  
#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int data;
    struct Node* next;
} Node;

typedef struct {
    Node* front; // 队头指针
    Node* rear; // 队尾指针
} Queue;

Queue* createQueue() {
    Queue* queue = (Queue*)malloc(sizeof(Queue));
    queue->front = NULL;
    queue->rear = NULL;
    return queue;
}

int isEmpty(Queue* queue) {
    return (queue->front == NULL);
}

void enqueue(Queue* queue, int data) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->data = data;
    newNode->next = NULL;
    
    if (isEmpty(queue)) {
        queue->front = newNode;
        queue->rear = newNode;
    } else {
        queue->rear->next = newNode;
        queue->rear = newNode;
    }
}

int dequeue(Queue* queue) {
    if (isEmpty(queue)) {
        printf("Queue is empty. Unable to dequeue.\n");
        return -1; // 返回一个表示错误的特殊值
    }
    
    int data = queue->front->data;
    Node* temp = queue->front;
    
    if (queue->front == queue->rear) {
        queue->front = NULL;
        queue->rear = NULL;
    } else {
        queue->front = queue->front->next;
    }
    
    free(temp);
    return data;
}

void traverse(Queue* queue) {
    if (isEmpty(queue)) {
        printf("Queue is empty. Nothing to traverse.\n");
        return;
    }
    
    printf("Queue traversal:\n\t\t");
    Node* current = queue->front;
    while (current != NULL) {
        printf("%d ", current->data);
        current = current->next;
    }
    printf("\n");
}

int main() {
    Queue* queue = createQueue();
    
    enqueue(queue, 5);
    enqueue(queue, 10);
    enqueue(queue, 3);
    
    traverse(queue);
    
    int data = dequeue(queue);
    printf("Dequeued data: %d\n", data);
    
    traverse(queue);
    
    return 0;
}

把 永 远 爱 你 写 进 诗 的 结 尾 ~ 文章来源地址https://www.toymoban.com/news/detail-478734.html

到了这里，关于【数据结构与算法】03 队列（顺序队列--循环队列--优先级队列--链队列）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！