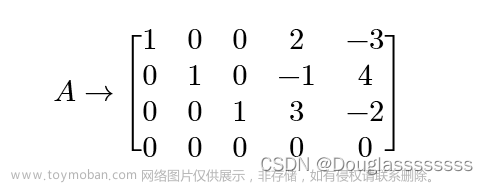
一、非齐次线性方程组AX=b的最小二乘解
超定方程组无解是因为方程组包含了过多的约束条件，无法满足所有的约束条件，在这种情况下，方程组的某些方程必然是矛盾的，也就是说，他们描述的条件是不兼容的，无法同时满足。 所以求解超定方程组其实是一个拟合问题，其基本思想是最小化所有方程的误差平方和，从而得到最优的解！
矩阵A列满秩表示的意思：就是我们要求的q个变量x是互相无关的（没有向量可用有限个其他向量的线性组合所表示），必须要把这q个变量都求出来才行，不能说求出q-1个就能把q个变量决定。
然后说一下当矩阵A列满秩的第二种情况：p=q表示A矩阵是个方阵，又因为是列满秩，所以是一个满秩的方阵，由于满秩的性质那么A的行列式不等于0。这时候Ax=y这个方程就很好求了，方程左右乘A的逆，就有唯一解了。
我们要关注的求最小二乘解，就是当矩阵A列满秩的第三种情况p＞q：p＞q就是表示我给的约束要比你求的参数多。这个时候我们定义一个能量函数E(x)，让A和x乘完后与y越接近越好。即让Ax-y的总误差越接近于0越好。这个时候求出的解就叫最小二乘解。两根竖线是表示求向量的模或者看做L2范数。
因此对于线性最小二乘问题，只要ATA非奇异，就可以用上图的求解方法1求解（A列满秩已经保证了ATA非奇异了，因为A列满秩-》A满秩-》ATA可逆(非奇异））。ATA是否可逆取决于该A是否是满秩矩阵（PS：不管矩阵A是不是方阵，列的秩和行的秩都是一样的，所以是否满秩看列或行的一个秩即可），如果不是A满秩矩阵，说明约束不够，这个方法无效，如果可逆那么这个问题就有唯一解！（PS：矩阵非奇异通常也被称为可逆矩阵，是等价的概念！是指一个方阵的行列式不等于零。）
二、齐次线性方程组AX=0的最小二乘解
在这种情况下，要关注的求最小二乘解，同样是当矩阵A列满秩的第三种情况p＞q：这个时候我们同样还是用上面的求解方法1对x求偏导，然后令导数等于0，但我们发现这样求解出的未知数x向量其实是一个0向量，但多数情况下，我们对0解没有兴趣，我们想要的是非0解，所以必须给X加一个约束，让X在满足条件的情况下使得║AX║的平方最小，于是就构造了一个带约束的最小二乘问题。
三、非线性方程组的最小二乘解
非线性最小二乘求解的问题，如果未知数X列向量的元素都写成一次项的话，就不能把方程组的系数写成上述线性方程组中的矩阵A的形式了，这同时也说明了矩阵只适用于对X做线性变换的性质，对于做非线性变换的变换，矩阵表示不出来。（PS：矩阵的线性变换可以用来描述向量的旋转、缩放、投影等变换。）
文章来源：https://www.toymoban.com/news/detail-478799.html
Refer：线性方程组的最小二乘解文章来源地址https://www.toymoban.com/news/detail-478799.html
到了这里，关于线性方程组AX=b，AX=0以及非线性方程组的最小二乘解（解方程组-＞优化问题）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
