一.判断题
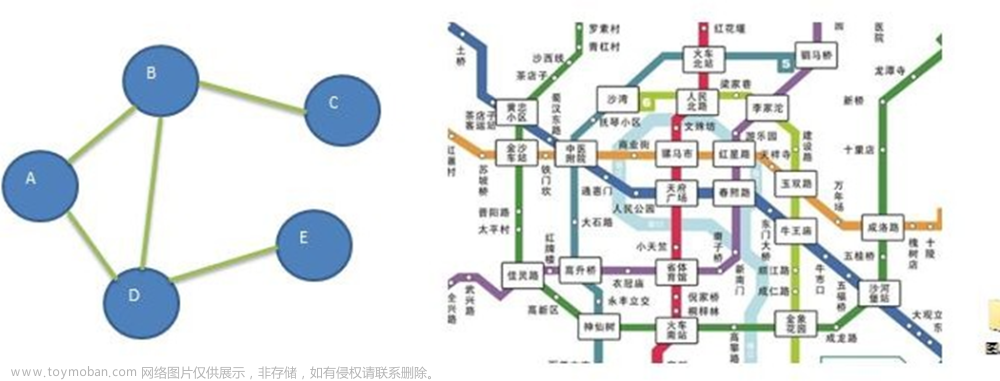
在一个有权无向图中,若b到a的最短路径距离是12,且c到b之间存在一条权为2的边,则c到a的最短路径距离一定不小于10。T
解析: 我们首先来分析b->a有几种可能,首先是b到a有直接的路径,其次b通过其他的结点到达a点。
如果是b通过c点到达a点我们就可以知道,min{b->c}+min{c->a}>=12;
但是我们知道min{b->c}<=2,因此12<=min{b->c}+min{c->a}<=2+min{c->a};
我们可以知道min{c->a}>=10;
————————————————
版权声明:本文为CSDN博主「你倒是敲代码啊.」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_43446165/article/details/102875160
如果 e 是有权无向图 G 唯一的一条最短边,那么边 e 一定会在该图的最小生成树上。T
Prim 算法是维护一个森林,每一步把两棵树合并成一棵。F
prim算法是通过每步添加一条边及其相连的顶点到一棵树,从而逐步生成最小生成树;
Kruskal 算法是维护一个森林,每一步把两棵树合并成一棵;
对于带权无向图 G = (V, E),M 是 G 的最小生成树,则 M 中任意两点 V1 到 V2 的路径一定是它们之间的最短路径。F
最小生成树的总权最小,不是其中的任意路径最小;
P 是顶点 S 到 T 的最短路径,如果该图中的所有路径的权值都加 1,P 仍然是 S 到 T 的最短路径。F
假如说最短路径上一共有10条边,而另一条路径虽然比最短路径长,但它只有一条边,如果全加1,就会导致边少的路径成为新的最短路径。
在图G的最小生成树G1中,可能会有某条边的权值超过未选边的权值。T
最小生成树的性质:
1.不唯一
2.边的权值总是唯一的,虽然最小生成树不唯一,但其对应的边的权值之和总是唯一的,而且是最小的。
3.最小生成树的边数为顶点数减1.
最小生成树总体权重值最小,可能会存在某条边的权值超过未选边的权值
最小生成树的KRUSKAL算法是一种贪心法(GREEDY)。T
二.单选题
1.Prim算法中dist数组中dist[i]存放的是( )
A.进入到顶点i的边上的最小权值
B.从顶点i出发的边上的最小权值
C.从起点到顶点i的最短路径长度
D.从顶点i到起点的最短路径长度
Prim算法
(2条消息) 最小生成树——Prim算法(详细图解)_skynesser的博客-CSDN博客
2.我们用一个有向图来表示航空公司所有航班的航线。下列哪种算法最适合解决找给定两城市间最经济的飞行路线问题?
A.深度优先搜索
B.Dijkstra算法
C.拓扑排序算法
D.Kruskal算法
深度优先/广度优先搜索——迷宫探索算法(2条消息) DFS深度优先搜索---最短路径问题全攻略,图文解析与算法实例
广度优先搜索(BFS)算法详解 (biancheng.net)
单源最短路径——Dijkstra算法
(2条消息) Dijkstra算法图文详解_black-hole6的博客-CSDN博客
最短路径算法全套(floyed+dijstra+Bellman+SPFA)_哔哩哔哩_bilibili
每对顶点最短路径——Floyd算法
Floyd算法详解 通俗易懂 - 知乎 (zhihu.com)
最短路径算法全套(floyed+dijstra+Bellman+SPFA)_哔哩哔哩_bilibili
拓扑排序算法
(2条消息) 拓扑排序及算法实现_拓扑排序算法_ShyTan的博客-CSDN博客
3.数据结构中Dijkstra算法用来解决哪个问题?
A.最短路径
B.字符串匹配
C.关键路径
D.拓扑排序
4.试利用Floyed算法,求下图所示有向图的各对顶点之间的最短路径。下列选项哪个给出了正确的最短路径长度矩阵和最短路径矩阵?
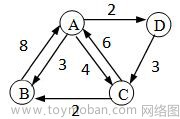
A.

B.

C.

D.

Floyed算法
最短路径算法全套(floyed+dijstra+Bellman+SPFA)_哔哩哔哩_bilibili
(2条消息) 【无标题】最短路径问题_试利用floyed算法,求下图所示有向图的各对顶点之间的最短路径。下列选项哪个给出_cuisl37186486的博客-CSDN博客
5.使用 Dijkstra 算法求下图中从顶点 1 到其余各顶点的最短路径,将当前找到的从顶点 1 到顶点 2、3、4、5 的最短路径长度保存在数组 dist 中,求出第二条最短路径后,dist 中的内容更新为:
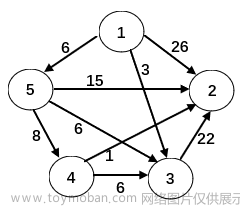
A.26、3、14、6
B.21、3、14、6
C.15、3、14、6
D.25、3、14、6
引用自:(2条消息) PTA算法 图练习题改错_无向图的邻接矩阵可用一维数组存储。_浮而不实的博客-CSDN博客
6. 给出如下图所示的具有 7 个结点的网 G,采用Prim算法,从4号结点开始,给出该网的最小生成树。下列哪个选项给出了正确的树结点收集顺序?
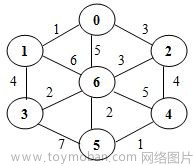
A.4526301
B.4563201
C.4501362
D.4561023
7.以下哪个不是给定无向带权图的最小生成树? A
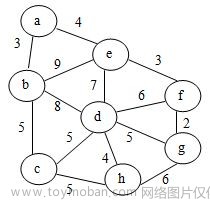
A.
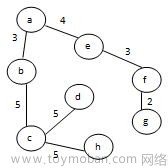
B.
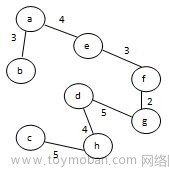
C.
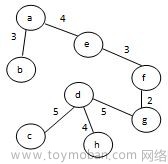
D.
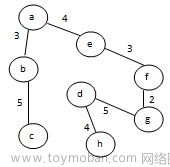
8.Prim算法通过( )方法保证不构成回路
A.BFS
B.并查集
C.DFS
D.标记数组
9.若要求在找到从S到其他顶点最短路的同时,还给出不同的最短路的条数,我们可以将Dijkstra算法略作修改,增加一个count[]数组:count[V]记录S到顶点V的最短路径有多少条。则count[V]应该被初始化为:
A.对所有顶点都有count[V]=0
B.count[S]=1; 对于其他顶点V则令count[V]=0
C.对所有顶点都有count[V]=1
D.count[S]=0; 对于其他顶点V则令count[V]=1
10.已知无向图 G 如下所示,使用克鲁斯卡尔(Kruskal)算法求图 G 的最小生成树,加入到最小生成树中的边依次是:

A.(a,e), (c,e), (b,e), (b,f), (b,d)
B.(b,f), (b,d), (a,e), (c,e), (b,e)
C.(a,e), (b,e), (c,e), (b,d), (b,f)
D.(b,f), (b,d), (b,e), (a,e), (c,e)
11.使用迪杰斯特拉(Dijkstra)算法求下图中从顶点1到其他各顶点的最短路径,依次得到的各最短路径的目标顶点是:
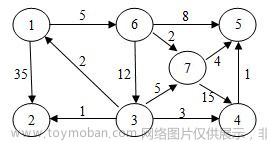
A.2, 4, 3, 6, 5, 7
B.2, 3, 4, 5, 6, 7
C.6, 2, 5, 7, 3, 4
D.6, 7, 5, 3, 2, 4
12.试利用 Dijkstra 算法求下图中从顶点 A 到其他顶点的最短距离及对应的路径。下列那个序列给出了可能的顶点收集顺序?
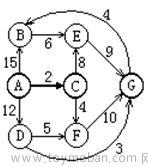
A.ACFEDBG
B.ACDBFEG
C.ABCDEFG
D.ACDGFBE
13.给定有权无向图的邻接矩阵如下,其最小生成树的总权重是:

A.17
B.18
C.23
D.24
三.填空题
下列代码的功能是使用Prim算法求出无向图的最小生成树权值总和,请补全。
给出的图用邻接矩阵存储。若两顶点之间没有直接路径,则对应权值为
INF,且题目保证 INF 值足够大;若找不到距离最短的顶点或者无法求出权值总和,则返回ERROR。文章来源:https://www.toymoban.com/news/detail-479230.html
(2条消息) 下列代码的功能是使用Prim算法求出无向图的最小生成树权值总和,请补全。_白术_竹苓的博客-CSDN博客文章来源地址https://www.toymoban.com/news/detail-479230.html
typedef int WeightType;
typedef int VertexType;
typedef struct {
int Nv;
WeightType G[MAX_GRAPH_SIZE][MAX_GRAPH_SIZE];
} GNode, * MGraph;
VertexType FindMinDist(MGraph Graph, WeightType dist[]) {
VertexType MinV = -1, V;
WeightType MinDist = INF;
for (V = 0; V < Graph->Nv; V++) {
if (dist[V] != 0 && dist[V] < MinDist) {
MinDist = dist[V];
MinV = V;
}
}
if (MinDist < INF) {
return MinV;
}
else {
return ERROR;
}
}
int Prim(MGraph Graph) {
int dist[MAX_GRAPH_SIZE];
int TotalWeight = 0, VCount = 0;
VertexType V, W;
for (V = 0; V < Graph->Nv; V++) {
dist[V] = Graph->G[0][V];
}
dist[0] = 0;
VCount++;
while (1) {
VertexType MinV;
if ((MinV = FindMinDist(Graph, dist)) == ERROR) {
break;
}
TotalWeight += dist[MinV];
dist[MinV] = INF;
VCount++;
for (W = 0; W < Graph->Nv; W++) {
if (dist[W] != 0 && dist[W] > Graph->G[MinV][W])
{
dist[W] = Graph->G[MinV][W];
}
}
}
if(!TotalWeight)
{
return ERROR;
}
else {
return TotalWeight;
}
}
到了这里,关于NeuDs 数据结构 图论的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!