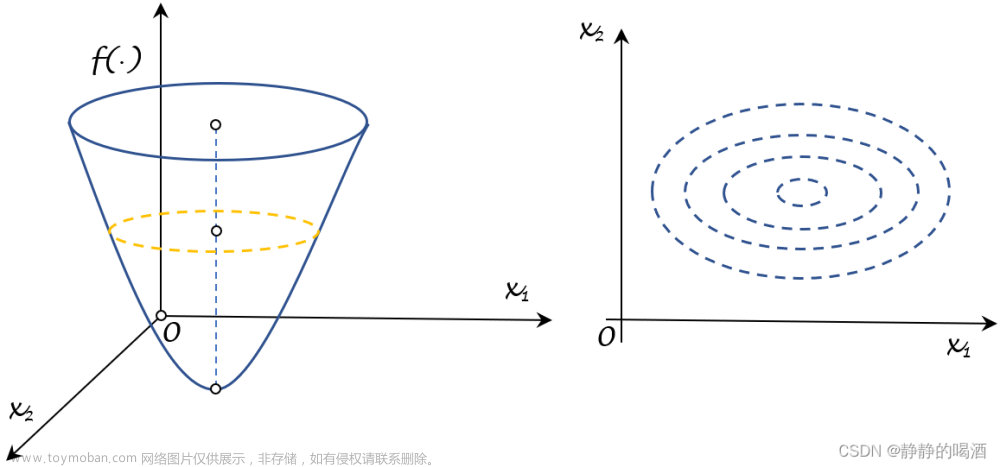
考虑下面线性方程组的求解问题，其中 x ∈ R n , b ∈ R m x\in \R^{n},b\in \R^{m} x∈Rn,b∈Rm，矩阵 A ∈ R m × n A\in \R^{m×n} A∈Rm×n，且向量 b b b的维数远小于向量 x x x的维数，也即 m m m<< n n n
A x = b Ax=b Ax=b
在相关问题中，当我们建立这样的模型后，常常希望解出向量 x x x，但无奈的是由于 m m m<< n n n，所以它会有无穷多解。但是，这些解当中大部分是不重要的，真正有用的是那些稀疏解
一：什么是稀疏优化
稀疏优化：原始信号中绝大多数元素为0，在某种线性约束条件下，求一个使决策变量使其非零元素个数达到最小，其基本数学模型如下
m i n ∣ ∣ x ∣ ∣ 0 , s . t . A x = b min||x||_{0},\quad s.t. \quad Ax=b min∣∣x∣∣0,s.t.Ax=b
这类技术常常应用于通过部分信息恢复全部信息。例如下图
- 假设读者评分仅与题材有关，那么就可以利用部分信息恢复全表
二：范数
范数（Norm）：在线性代数等数学学科中，范数是一个函数，其赋予某个向量空间或矩阵中的每个向量以长度或大小（对于零向量，令其长度为0）。直观来讲，向量或矩阵的范数越大，那么我们就可以说这个向量或矩阵也就越大
- 其实我们所熟知的绝对值也是范数，它是一维向量空间中实数或复数的范数
- 经常用到的欧氏距离也是范数
对于这三个范数，从效果上来看
- l 0 l_{0} l0效果最好
- l 1 l_{1} l1效果次之
- l 2 l_{2} l2效果最差
对于这三个范数，从求解速度上来看
- l 0 l_{0} l0基本很求解
- l 1 l_{1} l1也很难求解，运算时间较长，但要是能求出来，其解更偏向于全局最优解
- l 2 l_{2} l2求解速度较快，但容易陷入局部最优
（1） l 0 l_{0} l0范数
l 0 l_{0} l0范数：是指向量中非0的元素的个数。如果我们用 l 0 l_{0} l0范数来规则化一个参数矩阵 W W W的话，就是希望 W W W的大部分元素都是0，换句话说，让参数 W W W是稀疏的。所以 l 0 l_{0} l0范数非常适合机器学习中的稀疏编码，可以通过最小化 l 0 l_{0} l0范数来寻找最少的稀疏特征项
- 例如向量 a = [ 1 , 0 , 2 , 0 , − 1 , 2 ] a=[1, 0, 2, 0, -1 ,2] a=[1,0,2,0,−1,2]的 l 0 l_{0} l0范数就是4
但是， l 0 l_{0} l0范数的最小化问题是一个NP难问题，举个例子
- 假设某矩阵 A A A大小为500×2000，如果我们知道稀疏解为20（也即该矩阵中只有20个元素非零），那么你要想求解这20个点就有3.0×1047种可能，假设每次测试需要1.0×10-9s，那么总共需要1.2×1031年才能得到答案
（2） l 1 l_{1} l1范数和 l 2 l_{2} l2范数
-
l 1 l_{1} l1范数：是指向量中各个元素绝对值之和。 l 1 l_{1} l1是 l 0 l_{0} l0范数的最优凸近似
-
l 2 l_{2} l2范数：是指向量中各个元素平方和然后开根
l 1 l_{1} l1范数最优化问题的解是稀疏性的，其倾向于选择很少的一些非常大的值和很多的不重要的小值。而 l 2 l_{2} l2范数最优化则更多的非常少的特别大的值，却又很多相对小的值，但其仍然对最优化解有重要的贡献。但从最优化问题解的平滑性来看， l 1 l_{1} l1范数的最优解相对于 l 2 l_{2} l2范数要少，但其往往是最优解，而 l 2 l_{2} l2的解很多，但更多的倾向于某种局部最优解
三：稀疏优化例子
在MATLAB环境中构造矩阵 A A A（128×256），其每个元素都服从高斯分布，精确解 u u u只有10%的元素非零，每一个元素也服从高斯分布
m = 128; n = 256;
A = randn(m, n);
u = sprandn(n, 1, 0.1);
b = A * u;
此时， u u u便是如下 l 0 l_{0} l0范数问题的最优解
m i n x ∈ R n ∣ ∣ x ∣ ∣ 0 s . t . A x = b \mathop{min}\limits_{x\in \R^{n}}\quad||x||_{0}\quad s.t. \quad Ax=b x∈Rnmin∣∣x∣∣0s.t.Ax=b
而前面说过，
l
0
l_{0}
l0范数优化问题是
N
P
NP
NP难问题，所以是不可能直接求解出来的，因此可以转为
l
1
l_{1}
l1范数优化问题，如下
m
i
n
x
∈
R
n
∣
∣
x
∣
∣
1
s
.
t
.
A
x
=
b
\mathop{min}\limits_{x\in \R^{n}}\quad||x||_{1}\quad s.t. \quad Ax=b
x∈Rnmin∣∣x∣∣1s.t.Ax=b
但是相关论文已经证明， l 1 l_{1} l1是 l 0 l_{0} l0范数的最优凸近似，也即若 A A A、 b b b满足一定条件，向量 u u u也是 l 1 l_{1} l1范数优化问题的唯一最优解。从这里我们可以看到优化这门学科可以在很大程度上降低待研究问题的困难程度
但如果改为 l 2 l_{2} l2范数优化问题呢，即求解如下优化问题
m i n x ∈ R n ∣ ∣ x ∣ ∣ 2 s . t . A x = b \mathop{min}\limits_{x\in \R^{n}}\quad||x||_{2}\quad s.t. \quad Ax=b x∈Rnmin∣∣x∣∣2s.t.Ax=b
虽然 l 2 l_{2} l2范数优化问题可以很快求解出来，但此时 u u u已经不是原问题的解了。这是因为 l 1 l_{1} l1范数优化问题可以保证解的稀疏性，但 l 2 l_{2} l2范数优化问题并不能保证文章来源：https://www.toymoban.com/news/detail-479449.html
文章来源地址https://www.toymoban.com/news/detail-479449.html
四：低秩矩阵恢复
到了这里，关于（最优化理论与方法）第一章最优化简介-第二节：最优化典型实例之稀疏优化和低秩矩阵恢复的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
