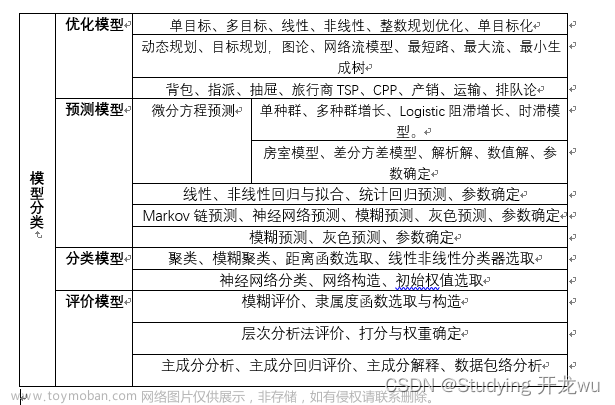
前言
2022年10月21日晴转多云转晴然后黑天了,不冷。今天有一件要紧的事要做,但我就是要先写完这个再去做。
1.(1)
题目
解微分方程
{
d
3
y
d
x
3
=
(
d
2
y
d
x
2
−
1
)
2
−
d
y
d
x
−
y
2
,
y
(
0
)
=
0
,
y
′
(
0
)
=
1
,
y
′
′
(
0
)
=
−
1.
\begin{cases} \dfrac{d^3y}{dx^3}=(\dfrac{d^2y}{dx^2}-1)^2-\dfrac{dy}{dx}-y^2, \\y(0)=0,y'(0)=1,y''(0)=-1. \end{cases}
⎩
⎨
⎧dx3d3y=(dx2d2y−1)2−dxdy−y2,y(0)=0,y′(0)=1,y′′(0)=−1.
(考虑
x
∈
[
0
,
20
]
x\in[0,20]
x∈[0,20],画出数值解及其一阶、二阶导数曲线图形).
代码
高阶微分方程,先化成一阶微分方程组,再求解。
令
y
1
=
y
,
y
2
=
y
′
,
y
3
=
y
′
′
y_1=y,y_2=y',y_3=y''
y1=y,y2=y′,y3=y′′,则原方程化为方程组
{
y
1
′
=
y
2
,
y
2
′
=
y
3
,
y
3
′
=
(
y
3
−
1
)
2
−
y
2
−
y
1
2
,
y
1
(
0
)
=
0
,
y
2
(
0
)
=
1
,
y
3
(
0
)
=
−
1.
\begin{cases} y_1'=y_2, \\y_2'=y_3, \\y_3'=(y_3-1)^2-y_2-y_1^2, \\y_1(0)=0,y_2(0)=1,y_3(0)=-1. \end{cases}
⎩
⎨
⎧y1′=y2,y2′=y3,y3′=(y3−1)2−y2−y12,y1(0)=0,y2(0)=1,y3(0)=−1.
所以在编写函数脚本文件时,要写成下面这样。
function dy=f1(t,y)
dy=[y(2);y(3);(y(3)-1).^2-y(2)-y(1).^2];
end
将上面的代码保存为f1.m。其中y是一个三列的向量,分量1为 y 1 y_1 y1,分量2为 y 2 y_2 y2,分量3为 y 3 y_3 y3。下面我们就要在ode45中调用f1啦:
[T,y]=ode45('f1',[0 20],[0 1 -1]);
plot(T,y(:,1),'-',T,y(:,2),'o',T,y(:,3),'x')
代码中[0 20]中的0是初值条件中的初值点,后面的[0 1 -1]是初值条件。画出的图像如下:
1.(2)
题目
求
{
d
y
d
x
=
−
0.01
y
−
99.99
z
,
d
z
d
x
=
−
100
z
,
y
(
0
)
=
2
,
z
(
0
)
=
1.
\begin{cases} \dfrac{dy}{dx}=-0.01y-99.99z, \\ \dfrac{dz}{dx}=-100z, \\y(0)=2,z(0)=1. \end{cases}
⎩
⎨
⎧dxdy=−0.01y−99.99z,dxdz=−100z,y(0)=2,z(0)=1.
的数值解,并画出数值解的图像。
代码
一样的,令
y
1
=
y
,
y
2
=
z
y_1=y,y_2=z
y1=y,y2=z,则有
{
y
1
′
=
−
0.01
y
1
−
99.99
y
2
,
y
2
′
=
−
100
y
2
,
y
1
(
0
)
=
2
,
y
2
(
0
)
=
1.
\begin{cases} y_1'=-0.01y_1-99.99y_2, \\y_2'=-100y_2, \\y_1(0)=2,y_2(0)=1. \end{cases}
⎩
⎨
⎧y1′=−0.01y1−99.99y2,y2′=−100y2,y1(0)=2,y2(0)=1.
function dy=f2(t,y)
dy=[-0.01*y(1)-99.99*y(2);-100*y(2)];
end
将上面这个代码保存为f2.m。调用:
[T,y]=ode45('f2',[0 500],[2 1]);
plot(T,y(:,1),'-',T,y(:,2),'.')
刚开始画的区间是0到20,但是很丑,很怪,不断调整区间,最终觉得0到500画出来的图还能入眼:
1.(3)
题目
求下列方程的通解及特解。
{
x
2
y
′
′
+
x
y
′
+
(
x
2
−
1
4
)
y
=
0
,
y
(
π
2
)
=
2
,
y
′
(
π
2
)
=
−
2
π
.
\begin{cases} x^2y''+xy'+(x^2-\dfrac{1}{4})y=0, \\y(\dfrac{\pi}{2})=2,y'(\dfrac{\pi}{2})=-\dfrac{2}{\pi}. \end{cases}
⎩
⎨
⎧x2y′′+xy′+(x2−41)y=0,y(2π)=2,y′(2π)=−π2.
代码
%求通解
y=dsolve('x.^2*D2y+x*Dy+(x.^2-1/4)*y=0','x');
disp('通解')
disp('y=')
pretty(y)
%求特解
y0=dsolve('x.^2*D2y+x*Dy+(x.^2-1/4)*y=0','y(pi/2)=2,Dy(pi/2)=-2/pi','x');
disp('特解')
disp('y0=')
pretty(y0)
用dsolve求解。求通解不需要写初值,求特解时要写初值。结果如下:

1.(4)
题目
已知 y ( 0 ) = − 0.2 , y ′ ( 0 ) = − 0.7 y(0)=-0.2,y'(0)=-0.7 y(0)=−0.2,y′(0)=−0.7用数值方法求 V a n d e r P o l Van\ der\ Pol Van der Pol方程 y ′ ′ + μ ( y 2 − 1 ) y ′ + y = 0 y''+\mu(y^2-1)y'+y=0 y′′+μ(y2−1)y′+y=0的解,并画出当 μ = 1000 \mu=1000 μ=1000时的图像。
代码
倦了。。。令 y 1 = y , y 2 = y ′ y_1=y,y_2=y' y1=y,y2=y′。So easy!!!
function dy=vdp1000(t,y)
dy=[y(2);-1000*(y(1).^2-1)*y(2)-y(1)];
end
保存为vdp1000.m。。。
[T,Y]=ode45('vdp1000',[0 0.05],[-0.2;-0.7]);
plot(T,Y(:,1),'-');
title('$Solution\ of\ van\ der\ Pol\ Equation,\mu=1000$','interpreter','latex');
哦,这里注意一下,最开始我给的区间是0到20,画出来的图巨丑,后来发现它就这么点好看的地方,我就把区间改成0到0.05咯。结果:
2.
题目
凶杀案作案时间问题:受害者的尸体于晚上7:30被发现,法医于晚上8:20赶到凶案现场,测得尸体温度为32.6℃;一小时后,当尸体即将被抬走时,测得尸体温度为31.4℃,室温在几个小时内始终保持21.1℃。此案最大的嫌疑犯张某声称自己是无罪的,并有证人说:“下午张某一直在办公室上班,5:00时打完电话后就离开了办公室”。从张某到受害者家(凶案现场)步行需5分钟,现在的问题是,张某不在凶案现场的证言能否被采信,使他排除在嫌疑犯之外。(提示:1、Newton冷却定理告诉我们“物体在介质中冷却速度同该物体温度与介质温度之差成正比” 2、自己假设人体的正常体温的温度值;3、求解非线性方程的MATLAB命令有fzero,solve)
代码
这个题目我们要求的是受害者死亡的时刻
t
0
t_0
t0。
首先介绍一下,%%在脚本文件中是分节符。在第一节,我们把体温随时间变化的关系式解出来了。将第一次测温的8:20作为0时刻,求解即可。运行第一节,我们得到关系式为
T
=
23
e
k
t
2
+
211
10
T=\dfrac{23e^{kt}}{2} + \dfrac{211}{10}
T=223ekt+10211
在第二节中,使用一小时后9:20的条件解出
k
k
k 的值。这里选择时间
t
t
t 的单位为小时,故
t
=
1
t=1
t=1,用solve解非线性方程即可,解出
k
k
k 的值赋给
k
0
k_0
k0 。
下面利用得到的特解
T
=
23
e
k
0
t
2
+
211
10
T=\dfrac{23e^{k_0t}}{2} + \dfrac{211}{10}
T=223ek0t+10211求温度
T
=
37
T=37
T=37 的时间
t
0
t_0
t0。为什么体温是37呢?因为人受到惊吓时体温会上升那么一丢丢。
%%求解温度变化曲线
clc,clear
T=dsolve('DT-k*(T-21.1)=0','T(0)=32.6','t')
%%
syms k
k0=solve((23*exp(k))/2 + 211/10-31.4==0);
syms t
t0=solve((23*exp(k0*t))/2 + 211/10-37==0);
time=8+1/3-ceil(abs(t0))+mod(t0,1);
a=sprintf('%d',floor(time));%时
b=sprintf('%d',floor(mod(time,1)*60));%分钟
disp(['案发时间为' a ':' b '左右'])
代码到time=…之前就已经把题目求解完了,后面只是将输出结果美化。blingbling美美哒的结果:
心机之蛙一直摸你肚子!案发时间是5:23左右,那么张某的嫌疑就无法排除了。文章来源:https://www.toymoban.com/news/detail-479788.html
总结
妹想到这么快又摸MATLAB了…心碎。随便做了做,若有错误请指正(抱拳)(充满侠气地离开)。文章来源地址https://www.toymoban.com/news/detail-479788.html
到了这里,关于数学实验课MATLAB实验报告二(题目+代码)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!