计算机视觉：转置卷积-Toy模板网

这篇具有很好参考价值的文章主要介绍了计算机视觉：转置卷积。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

转置卷积

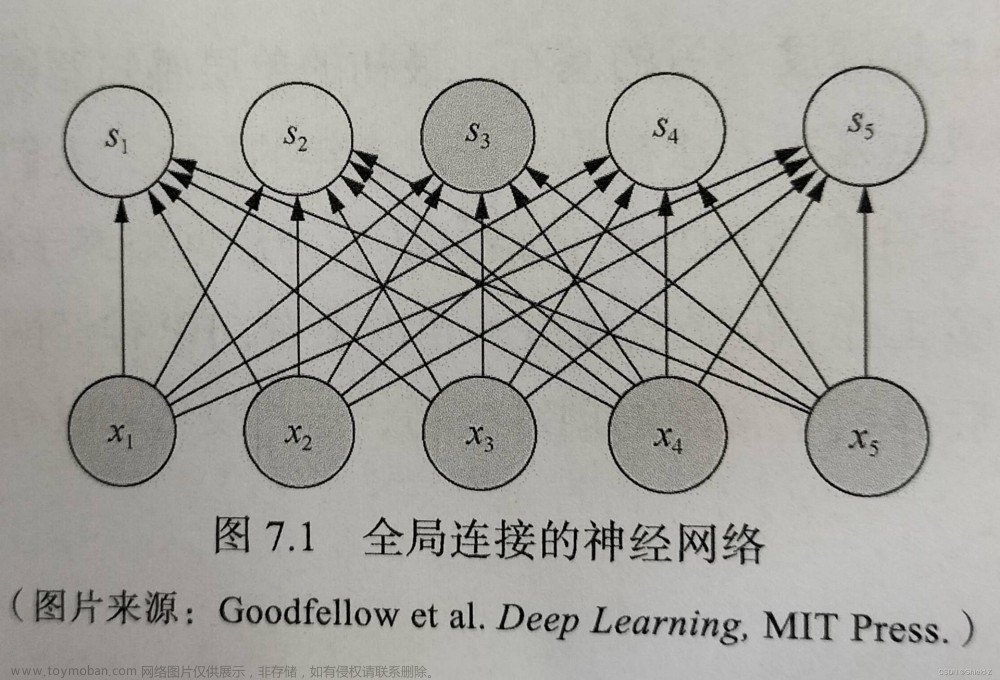
转置卷积（Transposed Convolution），也称为反卷积（Deconvolution），是卷积神经网络（CNN）中的一种操作，它可以将一个低维度的特征图（如卷积层的输出）转换为更高维度的特征图（如上一层的输入）。转置卷积操作通常用于图像分割、生成对抗网络（GAN）和语音识别等任务中。

在传统卷积操作中，我们使用一个滑动窗口（卷积核）来从输入图像中提取特征。而在转置卷积中，我们使用一个滑动窗口来填充零值的输出图像，然后通过卷积核来计算输出图像中每个像素的值。这个过程可以看作是对输入特征图进行上采样（增加分辨率）的过程。

具体来说，假设我们有一个输入特征图 $X$ ，大小为 $N\times N\times C$ ，其中 $N$ 是特征图的宽和高， $C$ 是特征图的通道数。我们还有一个大小为 $K\times K$ 的卷积核 $W$ ，其中 $K$ 是卷积核的大小。转置卷积的输出特征图 $Y$ 的大小为 $(N+2P-K+1)\times(N+2P-K+1)\times C'$ ，其中 $P$ 是填充大小， $C^{'}$ 是输出特征图的通道数。转置卷积的计算方式可以表示为：

$Y_{i,j,k} = \sum_{u=0}^{K-1}\sum_{v=0}^{K-1}\sum_{c'=1}^{C'} X_{i+u,j+v,c}W_{u,v,c',k}$

其中 $i, j$ 是输出特征图中的坐标， $k$ 是输出特征图中的通道数， $u, v$ 是卷积核中的坐标， $c$ 是输入特征图中的通道数， $c^{'}$ 是输出特征图中的通道数。

需要注意的是，转置卷积的输出特征图大小取决于填充大小 $P$ ，因此要根据具体的应用场景和网络结构来确定填充大小。另外，转置卷积还可以通过调整步长（stride）来控制输出特征图的大小。如果步长为 $S$ ，则输出特征图的大小为 $(N-1)\times S+K-2P$ 。

基本操作

让我们暂时忽略通道，从基本的转置卷积开始，设步幅为1且没有填充。假设我们有一个 $n_h\times n_w$ 的输入张量和一个 $k_h\times k_w$ 的卷积核。以步幅为1滑动卷积核窗口，每行 $n_h$ 次，每列 $n_w$ 次，共产生 $n_h\times n_w$ 个中间结果。每个中间结果都是一个 $(n_h\times k_h-1)\times (n_w\times k_w-1)$ 的张量，初始化为0。为了计算每个中间张量，输入张量中的每个元素都要乘以卷积核，从而使所得的 $k_h\times k_w$ 张量替换中间张量的一部分。请注意，每个中间张量被替换部分的位置与输入张量中元素的位置相对应。最后，所有中间结果相加以获得最终结果。

举个例子如下：
计算机视觉：转置卷积
我们可以对输入矩阵X和卷积核矩阵K实现基本的转置卷积运算trans_conv。

def trans_conv(X, K):
    h, w = K.shape
    Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1))
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            Y[i: i + h, j: j + w] += X[i, j] * K
    return Y

X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
trans_conv(X, K)

计算机视觉：转置卷积

或者使用torch自带的API：

X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False)
tconv.weight.data = K
tconv(X)

计算机视觉：转置卷积
nn.ConvTranspose2d 是 PyTorch 中用于创建转置卷积层的函数，它有以下参数：

in_channels：输入特征图的通道数。
out_channels：输出特征图的通道数。
kernel_size：卷积核的大小。可以是一个整数（表示正方形卷积核的边长），也可以是一个长度为 2 的元组或列表（表示长方形卷积核的宽和高）。
stride：卷积核的步长。可以是一个整数（表示在宽度和高度上的步长相同），也可以是一个长度为 2 的元组或列表（表示在宽度和高度上的步长分别为多少）。
padding：填充大小。可以是一个整数（表示在宽度和高度上的填充大小相同），也可以是一个长度为 2 的元组或列表（表示在宽度和高度上的填充大小分别为多少）。
output_padding：输出特征图的填充大小。可以是一个整数（表示在宽度和高度上的填充大小相同），也可以是一个长度为 2 的元组或列表（表示在宽度和高度上的填充大小分别为多少）。默认为 0。
groups：输入和输出通道之间的分组数。通常将其设置为 1，表示不进行通道分组。如果设置为大于 1 的值，则表示在输入和输出通道之间进行分组卷积。
bias：是否使用偏置。默认为 True，表示使用偏置。如果设置为 False，则不使用偏置。
dilation：卷积核的膨胀率。可以是一个整数（表示在宽度和高度上的膨胀率相同），也可以是一个长度为 2 的元组或列表（表示在宽度和高度上的膨胀率分别为多少）。默认为 1，表示不进行膨胀卷积。

填充、步幅和多通道

与常规卷积不同，在转置卷积中，填充被应用于的输出（常规卷积将填充应用于输入）。例如，当将高和宽两侧的填充数指定为1时，转置卷积的输出中将删除第一和最后的行与列。

tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, padding=1, bias=False)
tconv.weight.data = K
tconv(X)

计算机视觉：转置卷积
在转置卷积中，步幅被指定为中间结果（输出），而不是输入。使用上图中相同输入和卷积核张量，将步幅从1更改为2会增加中间张量的高和权重，因此输出张量在如下图：

tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, bias=False)
tconv.weight.data = K
tconv(X)

计算机视觉：转置卷积对于多个输入和输出通道，转置卷积与常规卷积以相同方式运作。假设输入有 $c_i$ 个通道，且转置卷积为每个输入通道分配了一个 $k_h\times k_w$ 的卷积核张量。当指定多个输出通道时，每个输出通道将有一个 $c_i\times k_h\times k_w$ 的卷积核。

性质

如果我们将 $X$ 代入卷积层 $f$ 来输出 $Y = f (X)$ ，并创建一个与 $f$ 具有相同的超参数、但输出通道数量是 $X$ 中通道数的转置卷积层 $g$ ，那么 $g (Y)$ 的形状将与 $X$ 相同。下面的示例可以解释这一点。

X = torch.rand(size=(1, 10, 16, 16))
conv = nn.Conv2d(10, 20, kernel_size=5, padding=2, stride=3)
tconv = nn.ConvTranspose2d(20, 10, kernel_size=5, padding=2, stride=3)
tconv(conv(X)).shape == X.shape

这个性质揭示了为什么这个操作被称为反卷积，因为它和卷积操作互逆

注意
1.数值不同，不可逆，形状可逆
2.效率高。原因：
①普通卷积操作的前向传播通过矩阵乘法一次实现，而非形式上的卷积核进行卷积并平移
②普通卷积操作的反向传播是输入乘转置权重矩阵
③上述代码表明，转置卷积作用实质上也是矩阵乘法，其前向传播为普通卷积的反向传播，反向传播同理文章来源地址https://www.toymoban.com/news/detail-479847.html

到了这里，关于计算机视觉：转置卷积的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！