Atcoder-AGC033C-Toy模板网

这篇具有很好参考价值的文章主要介绍了Atcoder-AGC033C。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

看到这道题，是个博弈论，没见过树上的，于是想到在数列里的博弈论，又联想到树的特殊形式————链。

于是我们来讨论一下链的情况（对于没有硬币的点，我们就视为它被删掉了）：

讨论链的情况

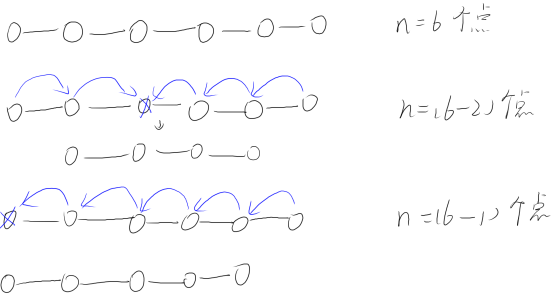
发现若是选择两端的点，顶点数会减一；若是选择中间的点，顶点数会减二。

现在我们站在链的角度来思考在树上选择的情况，一颗树可以看成一条链且在某些顶点上有分支的图。我们再来以这种方式来选点找找规律，发现树上的点删着删着最后总会变成一条链，且这条链是最长链的子链，于是我们把看这棵树的形式转换为其最长链（直径）且在某些顶点上有分支的图：

例子

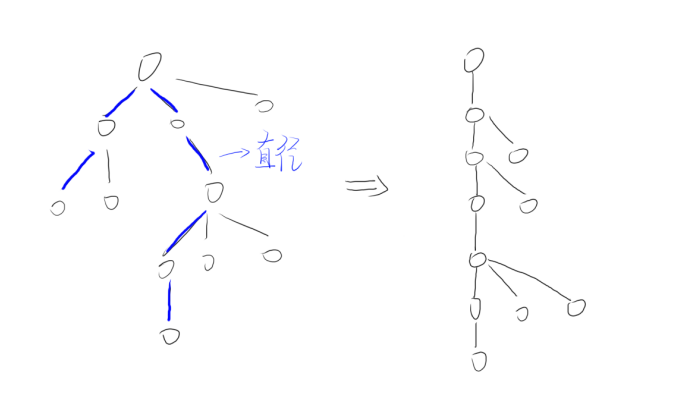
通过手玩这个例子后发现，我们若是选最长链两端的点，最长链顶点数会减一；若是选择非最长链两端的点，最长链顶点数会减二，其余的分支会因为持续的选点而被删完。

所以发现，在树上的问题被我们转化成了在链上的问题，妙哉！

讨论完了删点的变化情况，我们再来讨论一下必胜条件：若最长链上有 \(i-1\) 和 \(i-2\) 个点时均必胜，则最长链上有 \(i\) 个点时必败，否则必胜，特殊的，若最长链上有 \(1\) 个点时必胜，有 \(2\) 个点时必败。
打表发现用树的最长链上点的个数 \(\mod 3\) ，若等于 2 后手胜，否则先手胜。

Code：文章来源地址https://www.toymoban.com/news/detail-480039.html

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 2e5 + 5;

int n, x, y, fir, sec;
int la[N], en[N << 1], ne[N << 1], idx;

void add(int x, int y) {
	en[ ++ idx] = y; 
	ne[idx] = la[x];
	la[x] = idx;
}

void dfs(int u, int f, int step) {
	for (int i = la[u]; i; i = ne[i]) {
		int v = en[i];
		if(v == f) continue;
		if(fir < step) fir = step, sec = v; dfs(v, u, step + 1);
	}
}

int main(){
	ios::sync_with_stdio(0);
	cin >> n;
	for (int i = 1; i < n; ++ i ) cin >> x >> y, add(x, y), add(y, x);
	dfs(1, 0, 1); dfs(sec, 0, 1); 
	if((fir + 1) % 3 == 2) cout << "Second";
	else cout << "First";
	return 0;
}

到了这里，关于Atcoder-AGC033C的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！