1、概述
我们以电赛题板球控制系统为例,对多种PID系统的仿真结果图像进行分析,分析PID相关结构和参数对于仿真图像的影响。
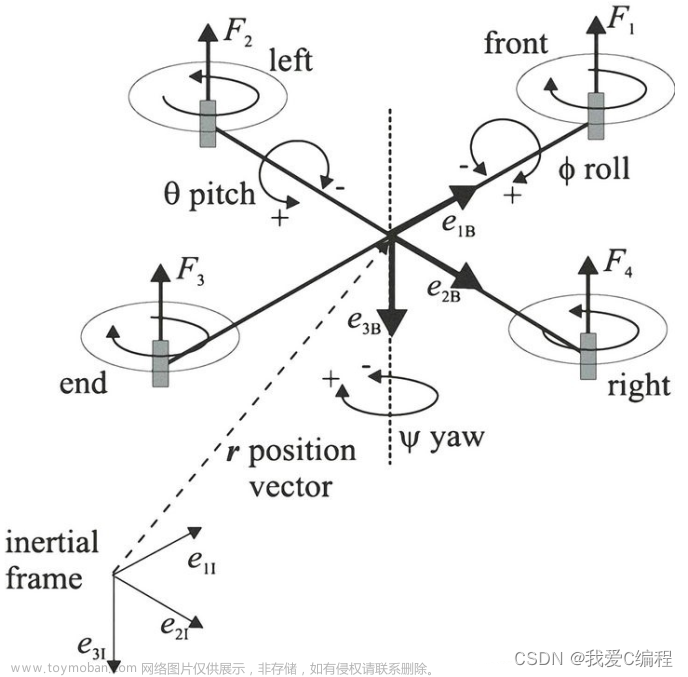
基本控制思路是:PID计算出给小球的加速度,通过舵机改变小球所在平面的角度,从而赋予小球相应的加速度,改变小球的速度,从而达到间接控制小球位置的效果。
我们分别使用了单环PID与双环PID,PID流程图分别如下:

此为单环PID流程图,给小球一个目标位置,计算出其与小球当前位置的差值,进行PID控制,将计算出的结果作为给小球的加速度。

此为双环PID流程图,给小球一个目标位置,对其与小球当前位置的差值进行PID控制,将计算出的结果作为给小球的目标速度,再对其与小球当前速度的差值进行PID控制,将计算出的结果作为给小球的加速度。
对于上述单双环PID,我们同时对连续时间和离散时间下的PID控制进行了分析,力求更好的拟合真实情况,在结果中我们可以看到,在离散时间下,双环PID能够很好的达到期望的效果。
2、单环PID控制
PID的基本调参思路:
1)将I和D都设为0,调节P,使得系统达到一个较为稳定的波动状态,一般来说,P的大小会改变系统自我调节的速度,从而影响系统变化的周期,P越大,系统自我调节速度越快。
2)调节好P之后,保持I=0不变,调节D,使得最后的位置变化曲线呈现美丽的S型,一般来说,D的作用是减小系统的波动,使系统走向收敛,D越大,系统容易出现收敛过于平缓的现象,D越小,系统会出现“过峰”现象。
3)一般来说,调节好P和D就够了,I可保持0不变,什么时候需要调节I呢?如果系统最后呈现出在目标值周围不断做小波动的情况时,也就是说系统基本达到目标值了,但是系统不能够稳定在目标值上时,我们可以给系统一点I,使系统稳定在目标值上。
利用MATLAB Simulink工具建立单环PID仿真系统:

用一个阶跃函数设置系统目标位置为200mm,在PID环节后,根据系统实际情况对加速度进行限幅,限制最大加速度为1.5m/s。
当PID三个参数分别为P=1,I=0,D=0时,示波器显示波形表现为简谐振动状态,可由微分方程 解释:
解释:

减小P,设置P=0.1,I=0,D=0,系统呈现出大周期的简谐运动状态,无法收敛。

增大D有助于减小系统的波动,使系统状态收敛。设置P=0.1,I=0,D=0.1,可以观察到系统状态开始慢慢收敛

继续增大D,当设置P=0.1,I=0,D=0.5时,系统呈现出一个较好的收敛状态:

但是可以注意到,小球的加速度在一瞬间发生突变,而现实情况下无法做到给小球一个突变的加速度。
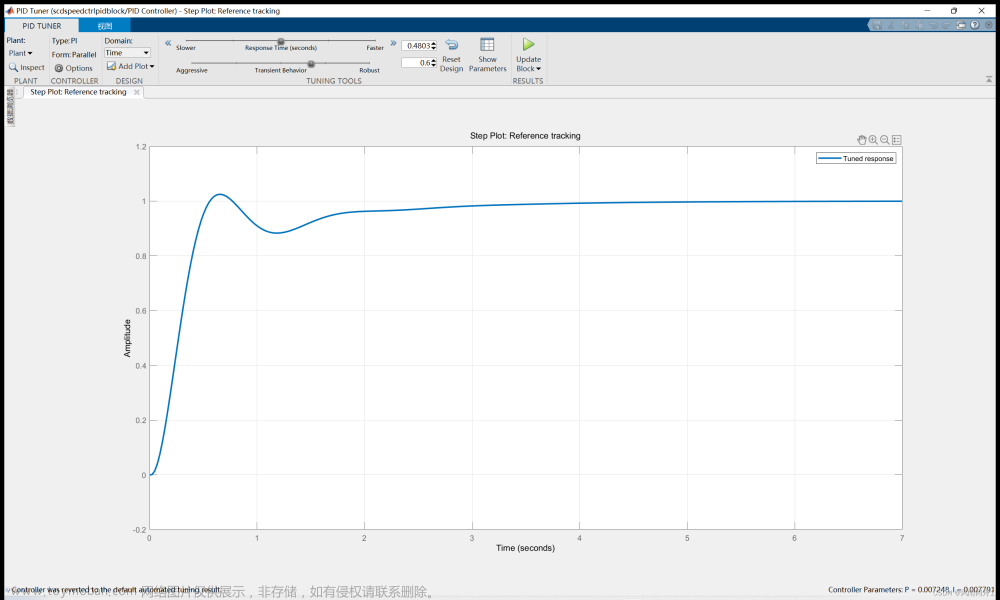
这实际上是由于我们上面的PID控制是基于连续时间条件的,而在现实情况下,由于控制小球变速的舵机有50Hz的控制频率,并且检测小球当前位置的相机有图像采集帧率,我们无法做到连续时间条件下的PID控制。因此,结合实际情况,接下来我们将采用离散时间条件下的PID控制,设置PID的离散时间间隔为0.05s,仿真系统如下,其中P=75,I=0,D=20,这个值是我们先进行几次大幅度简单调试后得到的。



仿真结果如上图所示,可以观察到最上方加速度的变化存在多次上下波动,减小p可以减少加速度的波动变化,我们将p重新设置为35,I继续保持为0,此时D=10比较合适(先设置P,根据P的值对D进行相应调节,使位置变化曲线呈现标准S型),可观察到如下仿真结果:

发现加速度的上下波动减少了,但是后阶段变化变得比较平滑,变化幅度小但是变化次数多,我们希望加速度的变化调节越少越好,于是我们再将P增大一些,设置P=41,I=0,D=10.3,仿真图像如下所示:

发现中间的速度变化曲线呈现出美丽的三角形,说明变化比较均匀,达到预期。
3、双环PID
在第二节中,我们使用单环PID使系统达到了较为理想的状态,但是,我们发现加速度曲线的调节变化次数仍然较多,使用双环PID可以对系统进行进一步的优化,双环PID的流程在第一节中已经给出了介绍,下面是在Simulink中搭建的双环PID系统

双环PID系统包括内环与外环,内环是一个速度PID,外环是一个位置PID。双环PID的调节分为两步,先单独拿出内环PID进行调节,使得内环PID达到理想状态,然后再将此时内环PID的参数代入双环PID系统中,调节外环PID参数,使得整个系统达到理想状态。要注意,内环PID的调节速度要大于外环,而P值决定了PID系统的调节速度,P值越大,PID系统调节越快,因此内环PID的P值要大于外环PID的P值。
先对内环PID进行调节:

我们发现,当P=20,I=0,D=0时,系统就已经非常完美了,那么内环PID调节就大功告成了:

把内环的参数代入双环PID系统中的内环中,接下来只需要调节外环就OK了,P先调小一点,设为1,I和D设为0,结果如下:

发现加速度曲线变化后期呈现变化次数多变化平缓的特点,说明P小了,把P调大一点,调为10,结果如下:

发现加速度多次上下波动,说明P大了,经过几次尝试之后,发现P=4.6的时候比较合适:

速度图像呈现出完美的三角形,同时加速度的变化次数比较少,所以P=4.6,I=0,D=0就是一个很好的选择了,不需要再调节D,因为图像底部的位置变化曲线已经是一条优美的S型曲线了。文章来源:https://www.toymoban.com/news/detail-480098.html
4、总结
与连续时间下的PID相比,离散时间下的PID能够更好地拟合实际情况。双环式PID能够使系统更好的达到我们期望的变化效果,即加速度变化少,呈现上下两段阶跃式;速度变化平稳,呈现优美的三角形;位置变化迅速平稳,呈现优美的S型。下图是在离散时间下,我们使用双环PID达到的较为理想的结果:文章来源地址https://www.toymoban.com/news/detail-480098.html

到了这里,关于MATLAB Simulink PID仿真图像分析(单双环、连续与离散时间)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!