【排序算法】归并排序（C语言）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【排序算法】归并排序（C语言）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【排序算法】—— 归并排序（C语言）

一、归并排序的原理

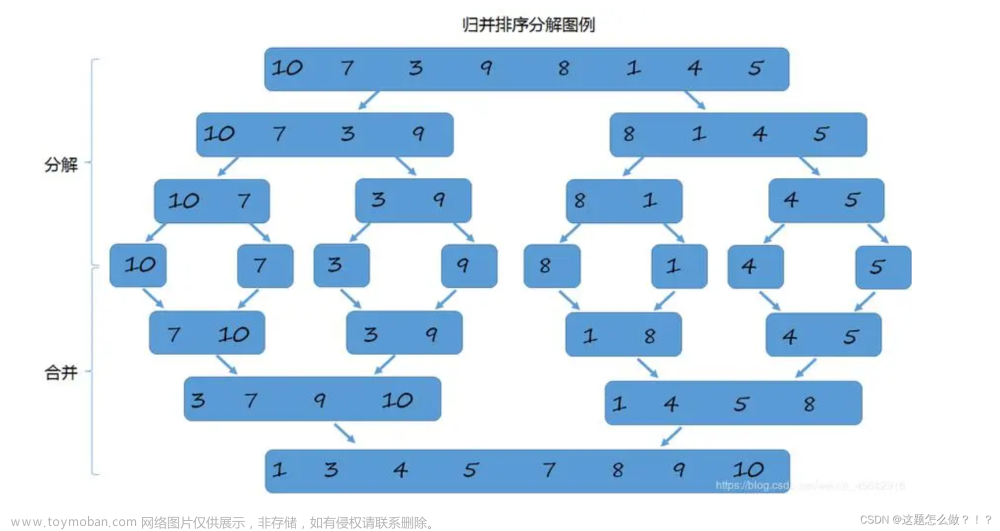
归并排序（MergeSort） 是建立在归并操作上的一种有效的排序算法，采用分治法排序，分为分解、合并两个步骤。

分解：将数组分割成两个数组，再分别将两个数组又细分成2个数组，直到，最后每个数组都是一个元素，这时将该单元素数组看为有序数组

合并：将分割的有序数组进行排序，排成有序数组后继续为上一个分割它的数组合并，直到数组被合并成原来的数组，此时已经排好序了

【排序算法】归并排序（C语言）

二、两个有序数组排序和合并

1. 原地排序

从头到尾遍历，选最小值放前面

合并的两个数组是一个数组分割开的，所以它们的首尾是相连的，用箭头i指向合并后数组的当前下标位置

【排序算法】归并排序（C语言）

将2和1比较，1小，所以将1赋值给合并后数组的第一个元素，此时我们发现，数组arr1的首元素被覆盖，所以不能直接赋值

【排序算法】归并排序（C语言）

若是将arr1的元素向后挪动一格，则数据正常，但是效率太低，不可取

【排序算法】归并排序（C语言）

从后往前遍历，选最大值放后面

用箭头i指向合并后数组的后边，从后往前遍历

【排序算法】归并排序（C语言）

8比7大，赋值给i指向的位置，此时7被覆盖，不行

【排序算法】归并排序（C语言）

若是将7和8交换呢，看样子可以，那如果是如下数组就不行了，arr1的有序性被破坏，不能继续这样排序了

【排序算法】归并排序（C语言）

2. 创建临时空间

既然无法原地排序，那我们创建临时空间，对两个有序数组排序

【排序算法】归并排序（C语言）

从前往后遍历，选出最小值放在temp数组前面部分

【排序算法】归并排序（C语言）

直到排序完成，将temp数组中的数据拷贝回原数组，arr1和arr2就合并成为有序数组arr

【排序算法】归并排序（C语言）

二、递归实现

我们使用递归来实现数组的分割和合并，它的逻辑非常像二叉树的后序遍历，由于我们要使用递归，又要申请临时空间，所以我们先申请好临时空间，再将归并排序过程作为子函数调用，这样不用在每次递归过程申请释放空间

归并排序调用递归

void MergeSort(int* arr, int size)
{
	int* temp = (int*)malloc(size * sizeof(int));
	if (temp == NULL)
	{
		perror("malloc fail\n");
		return;
	}

	_MergeSort(arr, 0, size - 1, temp);	//归并排序的过程

	free(temp);
	temp = NULL;
}

归并排序

由于我们递归过程中要用区间来分割函数，所以参数为待排数组的闭区间，使代码书写更加方便，这也是将递归过程单独调用的好处

void _MergeSort(int* arr, int left, int right, int* temp)
{
    //分解：
    //分割数组只有一个元素时停止递归
	if (left >= right)
	{
		return;
	}

	int mid = (left + right) / 2;

	_MergeSort(arr, left, mid, temp);		//分割并排序数组左半边
	_MergeSort(arr, mid + 1, right, temp);	//分割并排序数组右半边

    //合并：
	int begin1 = left, end1 = mid;			//数组1的左右区间
	int begin2 = mid + 1, end2 = right;		//数组2的左右区间
	int i = begin1;

    //排序两个有序数组
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (arr[begin1] <= arr[begin2])
		{
			temp[i] = arr[begin1];
			begin1++;
		}
		else
		{
			temp[i] = arr[begin2];
			begin2++;
		}
		i++;
	}

	while (begin1 <= end1)
	{
		temp[i] = arr[begin1];
		begin1++;
		i++;
	}

	while (begin2 <= end2)
	{
		temp[i] = arr[begin2];
		begin2++;
		i++;
	}

	//拷贝临时数组的内容到原数组（可以调用memcpy函数）
	//memcpy(arr+left, temp+left, (right-left+1)*sizeof(int));
	for (i = left; i <= right; i++)
	{
		arr[i] = temp[i];
	}
}

三、非递归实现

归并排序的非递归实现是非常复杂的一个算法，在快速排序中我们使用栈来存储待排数组的左右区间，模拟递归的过程。但是在归并排序中我们不这么实现。

1. 实现思路

由于数组总是以一半的方式进行分割，分割的终点是每个数组只有一个元素，所以我们可以定义一个变量gap作为分割后数组的长度，遍历时一次跳过gap * 2个元素，刚好是两个数组的长度，gap从1开始对两个有序数组进行排序，直到gap作为数组长度的一半时结束

令gap = 1，此时将长度为1的数组排序并合并，将两个长度为1的数组合并（黄色和蓝色分别是需要合并的两个数组）

【排序算法】归并排序（C语言）

排序合并后，将i指针向后移动gap * 2个元素，刚好两个数组，继续排序合并

【排序算法】归并排序（C语言）

持续上述操作，直到数组排序完成，则第一躺排序完成，所有长度为1的有序数组都合并成长度为2的有序数组

【排序算法】归并排序（C语言）

gap *= 2，一个数组长度为2，然后遍历数组，一次跳过2个有序数组（4个元素），并将两个有序数组排序合并

【排序算法】归并排序（C语言）

gap *= 2，一个数组长度为4，然后遍历数组，一次跳过2个有序数组（8个元素），并将两个有序数组排序合并

【排序算法】归并排序（C语言）

gap *= 2，此时gap为8，等于数组长度，意味着没有第二个数组与长度为8的数组合并了，排序结束，数组有序

【排序算法】归并排序（C语言）

2. 数组边界问题

在归并排序的非递归实现中，我们要遍历数组，将两个长度为gap的数组排序合并，但是gap总是2的幂次方，这就导致数组长度不一定是gap * 2的倍数，这就导致两个数组在遍历到数组边界时会导致越界问题。所以我们要对数组的边界问题进行处理

对于归并排序合并的两个数组，有3种越界情况：

第一个数组越界

黄色和蓝色数组是需要合并的两个数组，第一个数组指的是黄色数组，第二个数组指的是蓝色数组

此时遍历到数组末尾时，第一个数组只有一个元素，但是需要合并的数组长度是2，所以第一个数组访问时会造成越界（第二个数组自然也越界）

【排序算法】归并排序（C语言）

第二个数组全部越界

此时遍历到数组末尾时，第一个数组的长度刚好到原数组的末尾，第二个数组不存在，访问第二个数组是回越界

【排序算法】归并排序（C语言）

第二个数组部分越界

此时第一个数组在数组内，第二个数组只有一部分在数组内，第二个数组存在但是长度没有gap，访问第二个数组时会越界

【排序算法】归并排序（C语言）

解决方法：

我们来解决这些数组越界问题的方法是调整数组区间范围：

第一个数组越界时，第二个数组不存在，所以不用合并，第一个数组本身就是有序数组

第二个数组完全越界时，第二个数组依然不存在，所以不用合并

第三个数部分组越界时，第二个数组存在但是不完整，此时我们将第二个数组的结束位置调整为原数组末尾位置即可，让第一个数组和第二个数组合并。

3. 代码实现

先申请临时空间，然后根据gap遍历数组，依次排序合并数组。文章来源地址https://www.toymoban.com/news/detail-480357.html

void MergeSortNonR(int* arr, int size)
{
    //申请空间
    int* temp = (int*)malloc(size * sizeof(int));
    if (temp == NULL)
    {
        perror("malloc fail!\n");
        return;
    }
    
    //归并排序
    int gap = 1;
    while (gap < size)
    {
        //单趟排序
        int i = 0;
        for (i = 0; i < size; i += 2*gap)	//一次跨2*gap格，两个数组
        {
            int begin1 = i, end1 = i+gap-1;			//第一个数组下标区间
            int begin2 = i+gap, end2 = i+2*gap-1;	//第二个数组下标区间，别忘记加上i
            
            //数组边界处理
            if (end1 >= size)	//第一个数组越界
            {
                break;
            }
            if (begin2 >= size)	//第二个数组全部越界
            {
                break;
            }
            if (end2 >= size)	//第二个数组部分越界
            {
                end2 = size - 1;
            }
            
            //排序合并
            int j = i;	//合并后数组的下标
            while (begin1 <= end1 && begin2 <= end2)
            {
                if (arr[begin1] <= arr[begin2])
                {
                    temp[j] = arr[begin1];
                    begin1++;
                }
                else
                {
                    temp[j] = arr[begin2];
                    begin2++;
                }
                j++;
            }
            
            while (begin1 <= end1)
            {
                temp[j] = arr[begin1];
                begin1++;
                j++;
            }
            
            while (begin2 <= end2)
            {
                temp[j] = arr[begin2];
                begin2++;
                j++;
            }
            
            //拷贝temp数组到原数组（排哪个区间就拷贝哪个区间，end2是闭区间哦）
            for (j=i; j<=end2; j++)
            {
                arr[j] = temp[j];
            }
        }
        gap *= 2;
    }
    
    free(temp);
    temp = NULL;
}