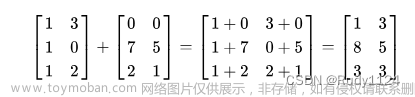
矩阵乘法,顾名思义是矩阵的乘法,矩阵相乘的含义是两个向量的积,在 Python中一般以乘号或括号表示。与常用的加、减、乘、除运算不同,矩阵乘法只能用于对给定矩阵进行乘法运算,不能进行除法运算。若要计算矩阵乘法的值,必须先进行矩阵分解。 在上一篇文章中,我们对矩阵乘法进行了初步学习,知道了求矩阵乘法的基本步骤: 1、初始化为0 2、令A=a*b 3、将a和b带入其中,并令a*b=0 4、令b=0,则A=(a*b)*(a-1) 10、令F=0,则A→(F-0)*F 11、若对a和b进行赋值也是求矩阵乘法。
-
一、初始化为0
初始化为0就是将矩阵A的所有元素初始化为0,若在 Python中使用空格代替输入,那么可以将输入的数字设置为空格。当然,我们也可以将矩阵A设置为: 在初始化之后,我们就可以计算出A*b了,这里的a和b分别代表的是A中的两个元素,即: 在上面的例子中,我们输入的数值为: 初始化为0后,矩阵A只有三个元素了: 此时,矩阵A就变成了一个完全的矩阵。 上面提到了“一个完全的矩阵”这一概念,那么如果想要得到矩阵乘法的值时是不是也要初始化为0呢?其实不是。我们在上面的例子中初始化后A并没有将其设置为0,所以最终得到的A值为:
-
二、令A=a*b
首先我们先来看一下 Python的矩阵运算是怎么进行的。在上一篇文章中,我们介绍了矩阵运算的两个基本操作,分别是将一个向量表示为另一个向量的“向量”,以及将一个向量与另一个向量进行相乘。根据矩阵分解定理,矩阵乘法的基本步骤如下: 5、将f的值赋给a和b; 6、对上述代码进行简化: 上面代码中的f'(x)是矩阵乘法的运算符,意思是“向量x”和“向量a”之间进行相乘。因此,我们将f=a*b简化为f=a*b+1,并赋给f'(x)。对f赋值后,我们就可以得到以下代码: 其中x是向量y的向量。
-
三、将a和b带入其中
我们上面提到,若对a和b进行赋值也是求矩阵乘法,那么这个运算能不能直接调用呢? 当然可以!在 Python中,我们可以通过赋值函数来实现向量之间的乘、加、减等运算,其中最常用的是赋值函数。 例如,下面是一个使用赋值函数实现矩阵乘法的例子: 这个例子中,我们使用了一个赋值函数(sum),将a和b带入其中。 在 Python中,我们可以使用赋值函数来进行矩阵乘法的运算: 在上面的代码中,我们先将a和b带入其中,然后再将其赋值给f (a): 在这里我们使用了一个特殊的赋值函数 sum来计算f (a)=f (a)*f (b),其中f (a)表示求出的矩阵,f (b)表示将矩阵转化为向量。
-
四、令a*b=0
2、运行该程序,输出结果: 3、通过上面的代码可以看出,矩阵乘法就是用括号中的字母表示一个矩阵,中元素的个数,对于任何一个矩阵乘法都可以写成: 4、当矩阵a*b=0时,我们就可以使用 sum ()函数来计算A的值了。 5、但是不能直接用 sum ()函数来计算A,因为矩阵a*b=0不是一个可积函数,我们必须使用 float ()函数。在上面的代码中,我们只需要让a*b=0就可以了。 6、对于矩阵乘法,还有一个关键点就是要注意初始化为0,如果初始化为0不成功,则无法继续进行下去。
-
五、令b=0
这个结果不够准确,因为我们在将a和b带入其中时,将a*b的值设置为0。上述代码中的第一个参数“+”是赋值给变量“a”的意思;第二个参数“-”是赋值给变量“b”的意思。当将a和b带入其中时,这两个参数并不会自动变成0。因为当我们把a和b带入其中时,它们并不会自动变成0,而是需要手动将其赋值为0才能使其成为0。这就是为什么要先令其变为0。 例如: 这种情况下我们就不能使用赋值运算符“+”了,而是要使用“-”。下面我们来看一道简单的计算题: 上面这个算式很容易理解: 这道算式告诉我们,当我们对变量进行赋值时,需要手动将其赋值为0才能使其成为0。那么正确的做法是如何做呢?
-
六、则A=(a*b)*(a-1)10
这道题目的原理其实很简单,就是在计算A时,先把矩阵分解成a*b的形式,再利用A=a*b的形式计算A,而不是直接用A*(a-1)=10。 接下来,我们开始练习一下矩阵乘法吧! 1、初始化为0:将矩阵初始化为0,并令a和b分别为0和1; 2、令a和b分别为0和1:将a、b带入矩阵中,并令它们分别为0和1; 5、对a和b进行赋值:分别对a、b赋值为0,并令它们的值分别为“1”和“0”; 6、计算A与A*(1+10)的积: 7、最后输出结果:
-
七、令F=0,则A→(F-0)*F 11
在上一篇文章中,我们将矩阵分解为多个向量的乘积,但是对于矩阵乘法,我们仍然可以将其视为对多个向量进行相乘。但是矩阵乘法的结果不能像对向量进行相乘那样将其赋值。 在上一篇文章中,我们介绍了如何通过赋值来对矩阵进行相乘。赋值的含义是:先将矩阵的一个元素(即向量)赋给一个向量(即矩阵),然后再将矩阵中的其他元素(即向量)赋给另一个向量(即矩阵),从而将多个向量相乘。 在上一篇文章中,我们知道了如何对一个矩阵赋值,但是在这里我们需要先将矩阵赋值给另一个向量。 例如:输入"a"和"b",然后对a和b进行赋值,得到如下的代码: 可以看出,此时输出的结果就是矩阵相乘的结果。与直接赋值相比,这种赋值方式更加方便、快捷。 上面的代码是可以实现对一个矩阵进行赋值的,但是这种赋值方式并不通用。而对于一个矩阵赋值为"a"和"b",输出的结果并不会改变。
-
常用的python矩阵乘法代码:文章来源:https://www.toymoban.com/news/detail-480575.html
-
1. 使用numpy库中的dot函数实现矩阵乘法:
```python
import numpy as np
# 定义两个矩阵
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
# 矩阵乘法
C = np.dot(A, B)
print(C)
```
输出结果:
```
[[19 22]
[43 50]]
```
2. 使用Python自带的zip函数实现矩阵乘法:
```python
# 定义两个矩阵
A = [[1, 2], [3, 4]]
B = [[5, 6], [7, 8]]
# 矩阵乘法
C = [[sum(a * b for a, b in zip(row_a, col_b)) for col_b in zip(*B)] for row_a in A]
print(C)
```
输出结果:
```
[[19, 22], [43, 50]]
```
3. 使用for循环实现矩阵乘法:
```python
# 定义两个矩阵
A = [[1, 2], [3, 4]]
B = [[5, 6], [7, 8]]
# 矩阵乘法
C = [[0 for j in range(len(B[0]))] for i in range(len(A))]
for i in range(len(A)):
for j in range(len(B[0])):
for k in range(len(B)):
C[i][j] += A[i][k] * B[k][j]
print(C)
```
输出结果:
```
[[19, 22], [43, 50]]
```文章来源地址https://www.toymoban.com/news/detail-480575.html
到了这里,关于python矩阵乘法全面解读,python矩阵乘法常用代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!