(超详细)C++图的深度优先遍历、广度优先遍历（数据结构）-Toy模板网

这篇具有很好参考价值的文章主要介绍了(超详细)C++图的深度优先遍历、广度优先遍历（数据结构）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

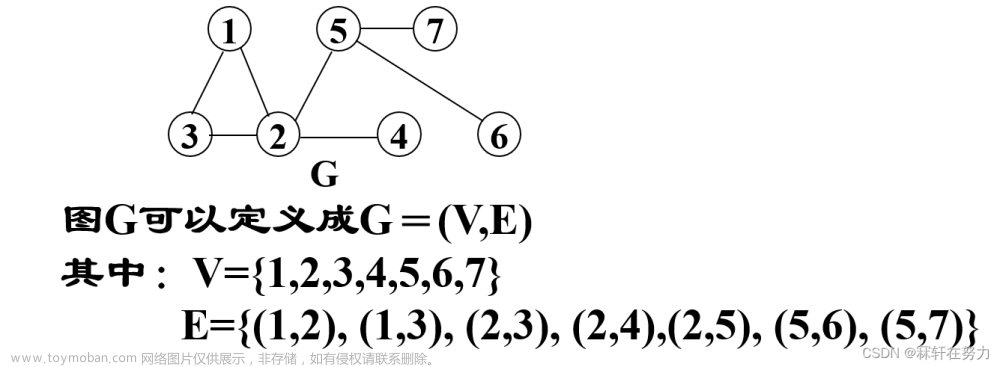
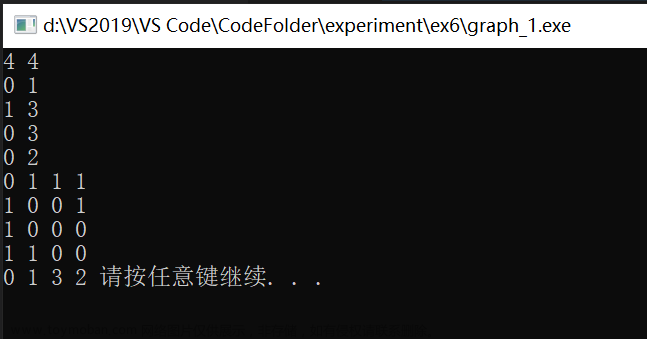
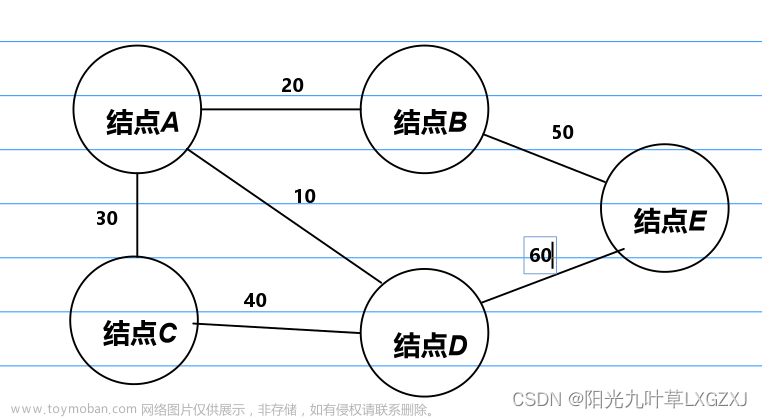
问题引入

根据下图，编写代码实现图的深度优先遍历和广度优先遍历。

按照英文字母顺序，以邻接表为存储结构，实现图的深度优先和广度优先遍历。遍历的顺序从顶点a开始。以用户指定的结点为起点，分别输出每种遍历下的结点访问序列。

(超详细)C++图的深度优先遍历、广度优先遍历（数据结构）

文章来源地址https://www.toymoban.com/news/detail-481454.html

一、代码实现

#include<iostream>
#include<malloc.h>
using namespace std;
#define MAX 20 //定义常量值为20 

int visited[MAX]; //定义标志数组（全局） 
 
//定义主结点结构（边界点） 
typedef struct Anode{
	int adjvex; //邻接点域（数据域） 
	struct Anode *next; //指向下一邻接点的指针域 
}ALnode;
//定义顶点表结点 
typedef struct vexnode{
	char data; //顶点域 
	ALnode *firstal; //指向第一条边结点 
}VexHeadNode;
//定义图的邻接表存储结构 
typedef struct{
	VexHeadNode adjlist[MAX]; //邻接表头结点数组 
	int n; //图的当前顶点数
	int e; //图的当前弧数，即边数 
}Graph;

//建立图的邻接表
void createGraph(Graph &G){
	int i,j,k; //辅助变量 
	ALnode *p; //辅助结点 
	cout<<"输入图的顶点数:";
	cin>>G.n;
	cout<<"输入图的边数:";
	cin>>G.e;
	cout<<endl; //换行 
	cout<<"输入图的各顶点(存储序号从0开始)："<<endl;
	for(i=0;i<G.n;i++){  //生成有n个顶点的顶点表
		cout<<"第"<<i<<"个顶点信息：";
		cin>>G.adjlist[i].data; //顶点数据存入表头 
		G.adjlist[i].firstal=NULL; //边表头指针域置为空 
	}
	cout<<endl; //换行 
	cout<<"输入图中的边，顶点序号从0开始:"<<endl;
	for(k=0;k<G.e;k++){
		cout<<endl; //换行 
		cout<<"输入第"<<k+1<<"条边:"<<endl;
		cout<<"输入出发顶点的序号：";
		cin>>i;
		cout<<"输入指向顶点的序号:";
		cin>>j;
		//邻接表存储连接 
		p=(ALnode *)malloc(sizeof(ALnode)); //分配存储空间 
		p->adjvex=j; //指向顶点的序号存入邻接点数据域 
		p->next=G.adjlist[i].firstal; //新的结点的指针域置为空 
		G.adjlist[i].firstal=p; //新结点信息依次存入邻接表中 
	}
} 

//输出邻接表
void printGraph(Graph G){
	int i; //辅助变量 
	ALnode *p; //辅助结点 
	cout<<"邻接表中的存储内容如下所示："<<endl;
	for(i=0;i<G.n;i++){
		cout<<i<<' '<<G.adjlist[i].data; //输出表头结点的数据 
		p=G.adjlist[i].firstal; //指向下一结点 
		while(p!=NULL){
			cout<<"--->"<<p->adjvex<<' '; //顺次输出结点信息 
			p=p->next;
		}
		cout<<endl; //换行 
	}
} 

//深度优先遍历
void DFSTraverse(Graph G,int v){
	ALnode *p; //辅助结点 
	cout<<"("<<v<<","<<G.adjlist[v].data<<")"<<' '; //输出顶点信息 
	visited[v] = 1;  
	p=G.adjlist[v].firstal; //访问第v个顶点
	while(p!=NULL){
		if(visited[p->adjvex]==0){
			DFSTraverse(G,p->adjvex);
		}
		p=p->next;
	} 
}

//广度优先遍历
void BFSTraverse(Graph G,int v){
	int i,j,visited[MAX]; //辅助变量、标志数组 
	ALnode *p; //辅助结点 
	int queue[MAX],front=0,rear=0; //定义循环队列  
	for(i=0;i<G.n;i++){  
		visited[i]=0; //标志数组信息初始化 
	} 
	cout<<"("<<v<<","<<G.adjlist[v].data<<")"<<' '; //输出顶点信息 
	visited[v]=1; //对应顶点的标志置为1 
	rear=(rear+1)%MAX; //队尾指针后移 
	queue[rear]=v; //查找的顶点对应序号入队列 
	//循环遍历 
	while(front!=rear){
		front=(front+1)%MAX; //队头指针后移
		j=queue[front]; //从队列中取出顶点对应序号 
		p=G.adjlist[j].firstal; //取对应序号的顶点信息 
		while(p!=NULL){ 
			if(visited[p->adjvex]==0){
				visited[p->adjvex]=1;
				cout<<"("<<p->adjvex<<","<<G.adjlist[p->adjvex].data<<")"<<' '; //输出顶点信息 
				rear=(rear+1)%MAX; //队尾指针后移 
				queue[rear]=p->adjvex; //查找的顶点对应序号入队列
			}
			p=p->next;
		}
	}
}

//主函数 
int main(){
	Graph G; //定义图结构变量 
	int v1,v2,choose; 
	cout<<"请选择：0-退出；1-创建有向图（采用邻接表存储结构）；2-深度优先遍历；3-广度优先遍历"<<endl;
	cin>>choose;
	while(choose!=0){
		switch(choose){
			case 1:{
				createGraph(G); //创建有向图 
				printGraph(G); //输出 
				break;
			}
			case 2:{
				cout<<"输入从哪个顶点开始遍历(序号从0开始)：";
				cin>>v1;
				DFSTraverse(G,v1);
				for(int i=0;i<G.n;i++){ 
					visited[i]=0; //标志数组信息初始化
				}
				cout<<endl;
				break;
			}
			case 3:{
				cout<<"输入从哪个顶点开始遍历(序号从0开始)：";
				cin>>v2;
				BFSTraverse(G,v2);
				cout<<endl;
				break;
			}
			default:cout<<"输入错误，请重新选择！"<<endl;
		}
		cout<<"请选择：0-退出；1-创建有向图（采用邻接表存储结构）；2-深度优先遍历；3-广度优先遍历"<<endl;
		cin>>choose;
	}
}