平面图
平面图的概念
一个平面图可能有多种平面嵌入，这些图之间都是同构的。
K 5 、 K 3 , 3 K_5、K_{3,3} K5、K3,3是非平面图。
一个平面图的有限面和无限面没有什么本质区别，可以相互转化。
- 自环所构成的面的边界长度为1
- 注意无限面的次数
一些性质：
- 割边只能是一个面的边界, 若一条边不是割边, 它必是两个面的公共边界
- 平面图𝐺中所有面的次数之和等于边数的2倍： ∑ d e g = 2 m \sum deg = 2m ∑deg=2m
- 欧拉公式： 顶点数 + 边数 − 面数 = 2 （注意：面数中包含无限面） , n − m + r = 2 顶点数+边数-面数 = 2（注意：面数中包含无限面）,\\n - m + r = 2 顶点数+边数−面数=2（注意：面数中包含无限面）,n−m+r=2
- （欧拉公式的拓展）对于任何具有 k k k个连通分支的平面图，有： 顶点数 − 边数 + 面数 = 连通分支数 + 1 , n − m + r = k + 1 顶点数-边数+面数 = 连通分支数+1,\\n-m+r = k +1 顶点数−边数+面数=连通分支数+1,n−m+r=k+1
- 若平面图各面的次数
d
d
d至少为3，则：
m
≤
d
d
−
2
(
n
−
2
)
m\le \frac{d}{d-2}(n-2)
m≤d−2d(n−2)（等号成立等价于各面的次数均为
d
d
d）.
可以用该必要条件判断一个图不是平面图。 - 平面图中都存在度数不大于5的顶点。
平面图的判定
充分条件：
- G 含 K 5 或 K 3 , 3 为子图 ⟹ G 是非平面图 G含K_5或K_{3,3}为子图\Longrightarrow G是非平面图 G含K5或K3,3为子图⟹G是非平面图。
- 若G满足 m < 9 或 n < 5 m<9或n<5 m<9或n<5，则是平面图。
同胚与收缩
若两个图是同构的，或经过多次插入、消去2度顶点后是同构的，则称这两个图同胚。
一个图是平面图的充要条件（Kuratowski定理）：
- G 是平面图 ⟺ G 不含与 K 5 同胚的子图，也不含与 K 3 , 3 同胚的子图 G是平面图\Longleftrightarrow G不含与K_5同胚的子图，也不含与K_{3,3}同胚的子图 G是平面图⟺G不含与K5同胚的子图，也不含与K3,3同胚的子图
- G 是平面图 ⟺ G 中不含可以收缩到 K 5 的子图，也不含可以收缩到 K 3 , 3 的子图 G是平面图\Longleftrightarrow G中不含可以收缩到K_5的子图，也不含可以收缩到K_{3,3}的子图 G是平面图⟺G中不含可以收缩到K5的子图，也不含可以收缩到K3,3的子图
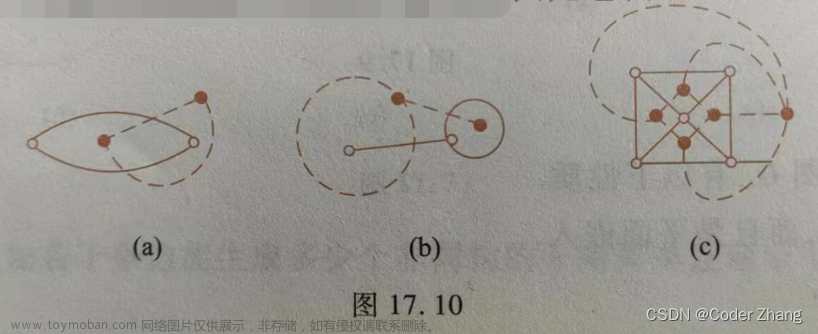
对偶图
对偶图的性质：
文章来源：https://www.toymoban.com/news/detail-481849.html
文章来源地址https://www.toymoban.com/news/detail-481849.html
到了这里，关于离散数学10：平面图与对偶图的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
