数据结构与算法—顺序表、链接表、顺序栈、链接栈、顺序队列、链接队列的C++代码实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构与算法—顺序表、链接表、顺序栈、链接栈、顺序队列、链接队列的C++代码实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1、线性表

线性表是一种常见的数据结构，具有以下几个特点：

元素的有限序列：线性表是由有限个元素组成的有序序列，每个元素的位置都是唯一确定的。

线性结构：线性表中的元素只有一个前驱和一个后继，除第一个和最后一个元素外，每个元素都有一个前驱和一个后继。

线性表可以用数组或链表来实现，数组的优点是支持随机访问，但在插入和删除元素时需要移动其他元素，效率较低；链表的优点是支持高效的插入和删除操作，但不支持随机访问。在实际应用中，根据不同的需求和场景，选择合适的实现方式可以提高算法效率和代码可读性。

1.1 顺序表–LinearList.h

#ifndef DATA_STRUCTURE_LINEARLIST_H
#define DATA_STRUCTURE_LINEARLIST_H

#include <iostream>
using namespace std;
template<class T>
class LinearList {
public:
    LinearList(int LLMaxSize);   //构造函数，创建空表
    ~LinearList();     //析构函数，删除表
    LinearList<T>& Insert(int k,const T& x);   //在第k个位置插入元素，返回插入后的空表

    bool IsEmpty() const;     //判断是否为空，表空返会true,表非空返回false
    int GetLength() const;    //返回表中数据元素的个数
    bool GetData(int k,T& x); //将表中第k个元素保存到x中，不存在则返沪false
    bool ModifyData(int k,const T&X);   //将表中第k个元素修改为x,不存在则返回false

    int Find(const T&x);     //返回x在表中的位置，如果x不在表中则返回0
    LinearList<T>& DeleteByIndex(int k,T&x);    // 删除表中第k个元素，并把保存到x中，返回删除后的线性表
    LinearList<T>& DeleteByKey(const T& x,T& y);    // 删除表中关键字为x的元素，并把保存到y中，返回删除后的线性表

    void OutPut(ostream& out) const;   //将线性表放到输出流out中输出
private:
    int length;      //当前数组元素个数
    int MaxSize;    //线性表中的最大元素个数
    T* element;     //一维动态数组
};


//
// Created by 22102 on 2023/3/26.
//

//实现构造函数
template<class T>
LinearList<T>::LinearList(int LLMaxSize){
    MaxSize = LLMaxSize;
    element = new T[LLMaxSize];
    length = 0;
}

//实现析构函数
template<class T>
LinearList<T>::~LinearList(){
    delete []element;
}

//实现插入新数据元素
template<class T>
LinearList<T>& LinearList<T>::Insert(int k,const T& x){
    if(k<1 || k>length+1){
        cout<<"元素下标越界，添加元素失败";
    }else{
        if(length==MaxSize){
            cout<<"此表已满，无法添加新元素";
        }else{
            for(int i=length;i<k-1;i--){
                element[i] = element[i-1];   //移动元素
            }
            element[k-1] = x;
            length++;
        }
    }
    return *this;
}

//实现是否判断为空表
template<class T>
bool LinearList<T>::IsEmpty() const{
    return length==0;
}

//实现求当前表的长度
template<class T>
int  LinearList<T>::GetLength() const{
    return length;
}

//实现按位置取元素
template<class T>
bool LinearList<T>::GetData(int k,T& x){
    if(k<1 || k>length){
        return false;
    }else{
        x = element[k-1];
        return true;
    }
}

//实现按位置修改元素
template<class T>
bool LinearList<T>::ModifyData(int k,const T& x){
    if(k<1 || k>length){
        return false;
    } else{
        element[k-1] = x;
        return true;
    }
}

// 实现按关键字查找
template<class T>
int LinearList<T>::Find(const T&x){
    for(int i=0;i<length;i++){
        if(element[i]==x){
            return i+1;
        }
    }
    return 0;
}

//实现按位置删除
template<class T>
LinearList<T>& LinearList<T>::DeleteByIndex(int k,T&x){
    if(GetData(k,x)){
        for(int i=k-1;i<length-1;i++){   //后面的元素往前移动
            element[i]=element[i+1];
        }
        length--;       //表长度减1
    }else{
        cout<<"元素下标越界，删除失败";
    }
    return *this;
}

//实现按关键字删除
template<class T>
LinearList<T>& LinearList<T>::DeleteByKey(const T& x,T& y){
    int index = Find(x);
    if(index !=0 ){
        return DeleteByIndex(index,y);
    }else{
        cout<<"没有此元素"<<endl;
        return *this;
    }

}

// 实现顺序表的输入
template<class T>
void LinearList<T>::OutPut(ostream& out)const
{
    for(int i=0;i<length;i++)
        out<<element[i]<<endl;
}
// 重载插入运算符 <<
template<class T>
ostream& operator<<(ostream& out,const LinearList<T>& x)
{
    x.OutPut(out);
    return out;
}

#endif //DATA_STRUCTURE_LINEARLIST_H

1.2 单向链表–LinkList.h

#ifndef DATA_STRUCTURE_LINKLIST_H
#define DATA_STRUCTURE_LINKLIST_H
#include <iostream>
using namespace std;
//存储节点类
template<class T>
class LinkNode{

    template<class U>
    friend class LinkList;   //将链式表类声明为友类
public:
    LinkNode(){     //构造函数
        next=NULL;
    }

private:
    T data;           //节点元素
    LinkNode<T>* next;    //指向下一结点的指针
};

//单向来链表类
template<class T>
class LinkList{
public:
    LinkList();    //构造函数
    ~LinkList();   //析构函数

    LinkList<T>& Insert(int k,const T& x);
    bool IsEmpty() const;
    int GetLength() const;
    bool GetData(int k,T& x);
    bool ModifyData(int k,const T&x);

    int Find(const T& x);
    LinkList<T>& DeleteByIndex(int k,T& x);
    LinkList<T>& DeleteByKey(const T& x,T& y);
    void OutPut(ostream& out);

private:
    LinkNode<T>* head;     //指向链表的第一个头结点的指针
};

//构造函数的实现
template<class T>
LinkList<T>::LinkList(){
    //创建空的单向链表
    head = new LinkNode<T>();  //创建头结点
}

//析构函数的实现
template<class T>
LinkList<T>::~LinkList(){
    // 空单向链表
    T x;
    int len = GetLength();
    for(int i=len;i>=1;i--){
        DeleteByIndex(i,x);   //释放所有结点
    }
    delete head;   //释放头结点
}

//实现插入新的数据元素
template<class T>
LinkList<T>& LinkList<T>::Insert(int k,const T& x)
{
    LinkNode<T> *p=head;//p指向头结点
    LinkNode<T> *newNode=new LinkNode<T>;//创建待插入的新结点
    newNode->data=x;
    int len=GetLength();
    if(k<1||k>len+1)
        cout<<"元素下标越界，添加元素失败";
    else
    {
        for(int i=1;i<k;i++){
            p=p->next;
        }
        newNode->next=p->next;
        p->next=newNode;
    }
    return *this;
}

//实现判断是否为空表
template<class T>
bool LinkList<T>::IsEmpty() const {
    return head->next == NULL;
}

//实现求当前链表的长度
template<class T>
int LinkList<T>::GetLength() const {
    int length=0;
    LinkNode<T> *p = head->next;
    while (p){
        length++;
        p = p->next;
    }
    return length;
}

// 实现按位置取元素
template<class T>
bool LinkList<T>::GetData(int k, T &x) {
    LinkNode<T> *p = head->next;
    int index =1;
    if(k<1 || k>GetLength()){
        return false;
    }
    while(p!=NULL && index<k){
        index++;
        p=p->next;
    }
    if(p==NULL){
        return false;
    } else{
        x = p->data;
        return true;
    }
}

//实现按位置修改元素
template<class T>
bool LinkList<T>::ModifyData(int k, const T &x) {
    LinkNode<T>* p = head->next;
    int index =1;
    if(k<1 || k>GetLength()){
        return false;
    }
    while(p!=NULL && index<k){
        index++;
        p = p->next;
    }
    if(p==NULL){
        return false;
    } else{
        p->data =x;
        return true;
    }
}

//实现按关键字查找
template<class T>
int LinkList<T>::Find(const T &x) {
    LinkNode<T>* p =head->next;
    int index =1;
    while (p!=NULL && p->data!=x){
        p = p->next;
        index++;
    }
    if(p!=NULL){
        return index;
    } else{
        return 0;
    }
}

//实现按位置删除
template<class T>
LinkList<T>& LinkList<T>::DeleteByIndex(int k,T& x){
    if(GetData(k,x)){   //判断是否有此元素，如果存在，则将该元素值放入x中，并返回true
        LinkNode<T> *p = head;     //p指向头结点
        LinkNode<T> *q = NULL;    //q指向空指针
        //删除中间或最后的结点
        for(int i=1;i<k;i++){
            p=p->next;         //将p指针移动到第k-1个结点
        }
        q=p->next;    //q指向待删除的第k个结点
        p->next = q->next;   //将第k个结点从链表中移出
        delete q;   //物理删除该结点
    }else{
        cout<<"元素下标越界，删除失败\n";
    }
    return *this;
}

//实现按关键字删除
template<class T>
LinkList<T>& LinkList<T>::DeleteByKey(const T &x, T &y) {
    int index = Find(x);
    if(index !=0){
        return DeleteByIndex(index,y);
    }else{
        cout<<"没有此元素，删除失败\n";
        return *this;
    }
}

// 实现单向链表的输出
template<class T>
void LinkList<T>::OutPut(ostream& out)
{
    LinkNode<T>* p=head->next;
    while(p!=NULL)
    {
        out<<p->data<<endl;
        p=p->next;
    }
}

//重载插入运算符<<
template<class T>
ostream& operator<<(ostream& out,LinkList<T>& x){
    x.OutPut(out);
    return out;
}

2、栈

栈是一种后进先出（Last In First Out，LIFO）的数据结构，也就是说，最后压入栈的元素最先弹出栈。栈只允许在栈顶进行插入和删除操作。由于只有栈顶元素可见，所以栈具有较好的封装性，也就是说，外部无法直接访问栈中的其他元素。常见的应用场景包括表达式求值、函数调用、程序调试等。

2.1 顺序栈–LinearStack.h

#ifndef DATA_STRUCTURE_LINEARSTACK_H
#define DATA_STRUCTURE_LINEARSTACK_H

#include<iostream>
using namespace std;

template<class T>
class LinearStack{
public:
    LinearStack(int LSMaxSize);  //构造函数，创建空栈
    ~LinearStack();  //析构函数，删除栈
    bool IsEmpty();  //判断栈是否为空，空返回true,非空返回false
    bool IsFull();   //判断栈是否为满，满返回true,不满返回false
    int GetElementNumber();   //求栈中元素个数

    bool Push(const T&x);  //在栈顶插入元素x，插入成功返回true,不成功返回false
    bool Top(T& x);        //求栈顶元素的值并将其放入x中，成功返回true,不成功返回false
    bool Pop(T& x);       //从栈顶删除一个元素怒，并将该元素的值放入x中
    void OutPut(ostream& out);    //将顺序栈放到输出流out中输出

private:
    int top;      //用来表示栈底
    int MaxSize;  //栈中最大元素个数
    T* element;   //一维动态数组
};

//实现构造函数
template<class T>
LinearStack<T>::LinearStack(int LSMaxSize){
    MaxSize = LSMaxSize;
    element = new T[LSMaxSize];
    top = -1;
}

//实现析构函数
template<class T>
LinearStack<T>::~LinearStack(){
    delete []element;
}

//实现判断栈是否为空
template<class T>
bool LinearStack<T>::IsEmpty() {
    return top == -1;
}

//实现判断栈是否为满
template<class T>
bool LinearStack<T>::IsFull() {
    return top+1 == MaxSize;
}

//实现进栈
template<class T>
bool LinearStack<T>::Push(const T &x) {
    if(IsFull()){
        return false;
    }else{
        top++;
        element[top]=x;
        return true;
    }
}

//实现求栈顶元素
template<class T>
bool LinearStack<T>::Top(T &x) {
    if(IsEmpty()){
        return false;
    } else{
        x=element[top];
        return true;
    }
}

//实现出栈
template<class T>
bool LinearStack<T>::Pop(T &x) {
    if(IsEmpty()){
        return false;
    }else{
        x=element[top];
        top--;
        return true;
    }
}

//实现顺序栈的输出
template<class T>
void LinearStack<T>::OutPut(ostream &out) {
    for (int i = 0; i < top; ++i) {
        out<<element[i]<<endl;
    }
}

//重载插入运算符<<
template<class T>
ostream& operator<<(ostream& out,const LinearStack<T>& x){
    x.OutPut(out);
    return out;
}
#endif //DATA_STRUCTURE_LINEARSTACK_H

2.2 链接栈–LinkStack.h

#ifndef DATA_STRUCTURE_LINKSTACK_H
#define DATA_STRUCTURE_LINKSTACK_H
#include<iostream>
using namespace std;
//存储结点类
template<class T>
class LinkNode{
    template<class U>      //将链接栈声明为友类.使单向链栈类中的成员函数可以直接访问LinkNode对象中的私有成员。
            friend class LinkStack;
public:
    LinkNode(){    //构造函数
        next =NULL;
    }
private:
    T data;        //结点元素
    LinkNode<T>* next;   //指向下一个结点的指针
};


//单向链接栈类
template<class T>
class LinkStack{
public:
    LinkStack();      //构造函数，创建空栈
    ~LinkStack();    //析构函数，删除栈
    bool IsEmpty() const;   // //判断栈是否为空，空返回true,非空返回false
    bool Push(const T& x);  //在栈顶插入元素x，插入成功返回true,不成功返回false
    bool Top(T& x);      //求栈顶元素的值并将其放入x中，成功返回true,不成功返回false
    bool Pop(T& x);        //从栈顶删除一个元素怒，并将该元素的值放入x中

    void OutPut(ostream& out);   //将链接栈放到输出流out中输出
private:
    LinkNode<T>* top;    //指向链接栈的栈顶点的指针
    int size;    //栈元素个数
};

//实现构造函数
template<class T>
LinkStack<T>::LinkStack(){
    top = NULL;
    size =0;
}

//实现析构函数
template<class T>
LinkStack<T>::~LinkStack(){
    T x;
    while(top!=NULL){    // 栈非空则元素出栈
        Pop(x);
    }
}

//实现判断栈是否为空
template<class T>
bool LinkStack<T>::IsEmpty() const{
    return top==NULL;
}

//实现进栈
template<class T>
bool LinkStack<T>::Push(const T& x){
    LinkNode<T>* p = new LinkNode<T>;
    if(p==NULL){
        return false;
    }else{
        p->data = x;    //为元素辅助
        p->next = top;    //将新结点插入栈顶  (每次都是在头结点处插入)
        top = p;   // top指向栈顶
        size++;
        return true;
    }
}

//实现求栈顶元素
template<class T>
bool LinkStack<T>::Top(T& x){
    if(IsEmpty()){
        return false;
    }else{
        x = top->data;
        return true;
    }
}

//实现出栈
template<class T>
bool LinkStack<T>::Pop(T& x){
    LinkNode<T>* p;
    if(IsEmpty()){    //栈为空，则返回false，元素出栈失败
        return false;
    }else{
        x = top->data;
        p = top;
        top = top->next;
        delete p;       //释放栈顶元素的内存空间
        size--;
        return true;
    }
}

//实现链接栈的输出
template<class T>
void LinkStack<T>::OutPut(ostream& out){
    LinkNode<T>* p;
    p=top;
    for(int i=0;i<size;i++){
        out<<p->data<<endl;
        p=p->next;
    }
}

//重载插入运算符<<
template<class T>
ostream& operator<<(ostream& out,const LinkStack<T>& x){
    x.OutPut(out);
    return out;
}

#endif //DATA_STRUCTURE_LINKSTACK_H

3、队列

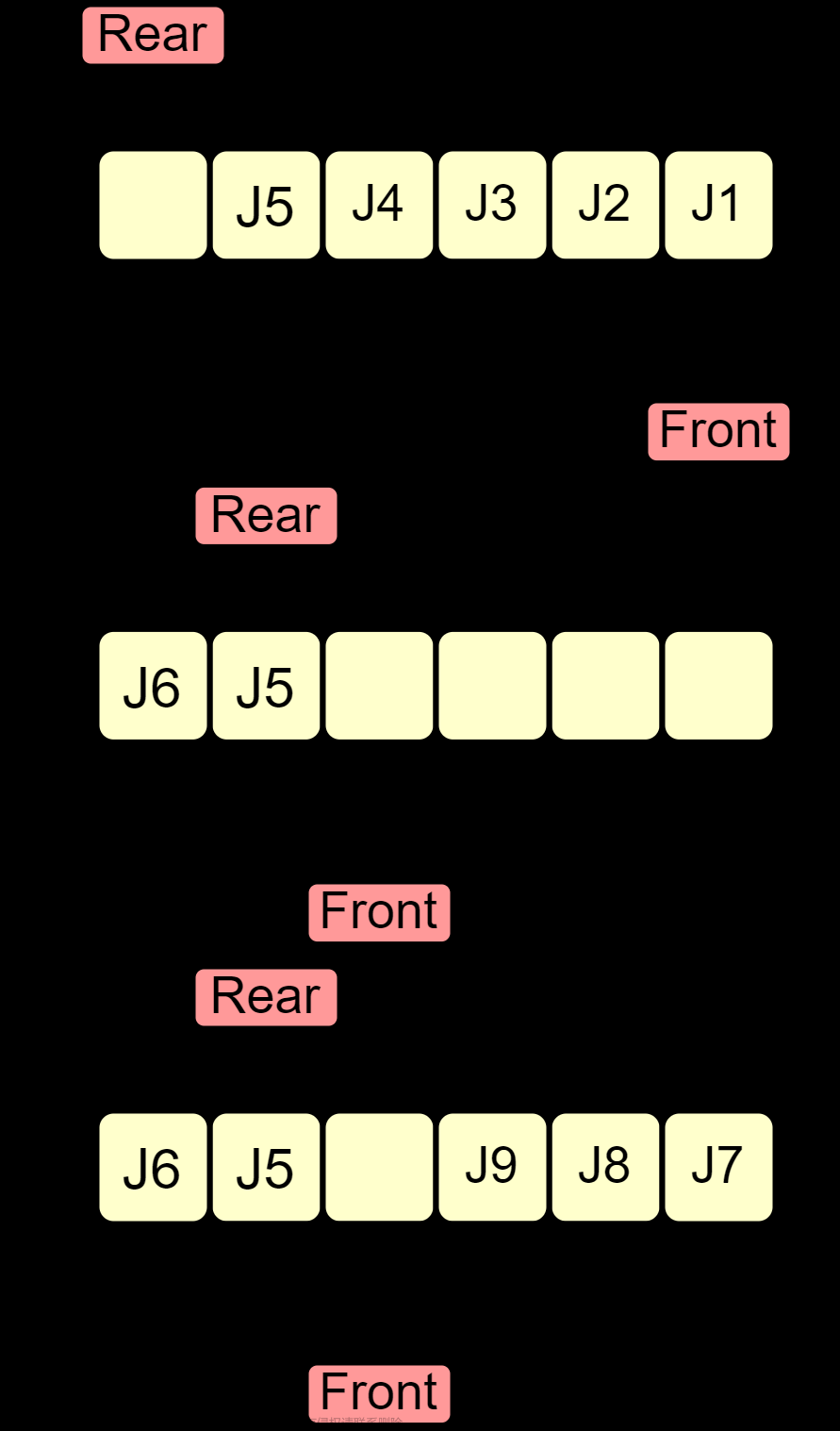
队列是一种先进先出（First In First Out，FIFO）的数据结构，也就是说，最先加入队列的元素最先被弹出队列。队列通常分为队头（front）和队尾（rear），只允许在队尾插入元素，在队头删除元素。队列具有较好的顺序性，也就是说，元素的顺序是有意义的。常见的应用场景包括消息队列、任务队列、缓冲区等。

3.1 顺序队列–LinearQueue.h

#ifndef DATA_STRUCTURE_LINEARQUEUE_H
#define DATA_STRUCTURE_LINEARQUEUE_H
#include<iostream>
using namespace std;
template<class T>
class LinearQueue{
public:
    LinearQueue(int LQMaxSize);    //创建空队列
    ~LinearQueue();    //删除队列
    bool IsEmpty();
    bool IsFull();
    bool Insert(const T& x);   //入队，在队列尾部插入元素x
    bool GetElement(T& x);   // 求队头元素的值并放入x中
    bool Delete(T& x);    //进队，从对头删除一个元素，并将该元素的值放入x中

    void OutPut(ostream& out) const;   //输出队列
private:
    int size;   //队列实际元素个数
    int MaxSize;   // 队列最大元素个数
    int front,rear;  // 队列的队头和队尾指针
    T* element;   //一维动态数组
};

//实现构造函数
template<class T>
LinearQueue<T>::LinearQueue(int LQMaxSize) {
    MaxSize = LQMaxSize;
    element = new T[MaxSize];
    size =0;
    front = 0;
    rear =0;
}

//实现析构函数
template<class T>
LinearQueue<T>::~LinearQueue(){
    delete []element;           //释放堆内存空间
};

//实现判断队列是否为空
template<class T>
bool LinearQueue<T>::IsEmpty(){
    return size == 0;
}

//实现是否判断队满
template<class T>
bool LinearQueue<T>::IsFull() {
    return size == MaxSize;
}

//实现入队
template<class T>
bool LinearQueue<T>::Insert(const T &x) {
    if(IsFull()){
        return false;
    } else{
        element[rear] = x;
        rear = (rear+1)%(MaxSize);
        size++;
        return true;
    }
}

//实现求队头元素
template<class T>
bool LinearQueue<T>::GetElement(T &x) {
    if(IsEmpty()){
        return false;
    }else{
        x = element[front];
        return true;
    }
}

//实现出队
template<class T>
bool LinearQueue<T>::Delete(T &x) {
    if(IsEmpty()){
        return false;
    } else{
        x = element[front];
        front = (front+1)%(MaxSize);
        size--;
        return true;
    }
}

//实现顺序队列的输出
template<class T>
void LinearQueue<T>::OutPut(ostream &out) const {
    int index;
    index = front;
    for(int i=0;i<size;i++){
        cout<<element[index]<<endl;
        index = (index+1) % MaxSize;
    }
}

//重载插入运算符<<
template<class T>
ostream& operator<<(ostream& out,LinearQueue<T>& x){
    x.OutPut(out);
    return out;
}
#endif //DATA_STRUCTURE_LINEARQUEUE_H

3.2 链接队列–LinkStack.h

#ifndef DATA_STRUCTURE_LINKQUEUE_H
#define DATA_STRUCTURE_LINKQUEUE_H

#include<iostream>
using namespace std;

//存储结点类
template<class T>
class LinkNode{
    template<class U>
            friend class LinkQueue;
public:
    LinkNode(){
        next = NULL;
    };
private:
    T data;  //结点元素
    LinkNode<T>* next;    //指向下一结点的指针
};


template<class T>
class LinkQueue{
public:
    LinkQueue();
    ~LinkQueue();
    bool IsEmpty();
    bool Insert(const T& x);
    bool GetElement(T& x);
    bool Delete(T& x);

    void OutPut(ostream& out) const;

private:
    int size;
    LinkNode<T>* front,*rear;
};

//实现构造函数
template<class T>
LinkQueue<T>::LinkQueue(){
    front = NULL;
    rear = NULL;
    size = 0;
}

//实现析构函数
template<class T>
LinkQueue<T>::~LinkQueue(){
    T x;
    while(front != NULL){    //队列非空则元素依次出队
        Delete(x);
    }
}

//实现判断队列是否为空
template<class T>
bool LinkQueue<T>::IsEmpty(){
    return size == 0;
}

//实现入队
template<class T>
bool LinkQueue<T>::Insert(const T& x){
    LinkNode<T>* p = new LinkNode<T>;
    if(p==NULL){
        return false;
    }else{
        p->data = x;    //为元素赋值
        // 将新进结点插入队尾
        if(front == NULL){   //插入前是空队列
            rear = p;
            front = p;
        }else{
            rear->next = p;
            rear = p;
        }
        size++;
        return true;
    }
}

//实现求对头元素
template<class T>
bool LinkQueue<T>::GetElement(T& x){
    LinkNode<T>* p;
    if(IsEmpty()){
        return false;
    } else{
        x=front->data;
        return true;
    }
}

//实现出队
template<class T>
bool LinkQueue<T>::Delete(T& x){
    LinkNode<T>* p;
    if(IsEmpty()){
        return false;
    } else{
        p=front;
        x=front->data;
        front = front->next;
        delete p;   //删除队头结点
        size--;
        return true;
    }
}

//实现链接队列的输出
template<class T>
void LinkQueue<T>::OutPut(ostream& out) const{
    LinkNode<T> *p;
    p=front;
    for (int i = 0; i < size; i++) {
        out<<p->data<<endl;
        p=p->next;
    }
}

//重载插入运算符
template<class T>
ostream& operator<<(ostream& out,const LinkQueue<T>& x){
    x.OutPut(out);
    return out;
}
#endif //DATA_STRUCTURE_LINKQUEUE_H