p 值计算（置信度）-Toy模板网

这篇具有很好参考价值的文章主要介绍了p 值计算（置信度）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、p值的概念

p 值计算（置信度）

参考【科研新手必学】手把手教你统计学的P值含义和检验假设

p 值计算（置信度）

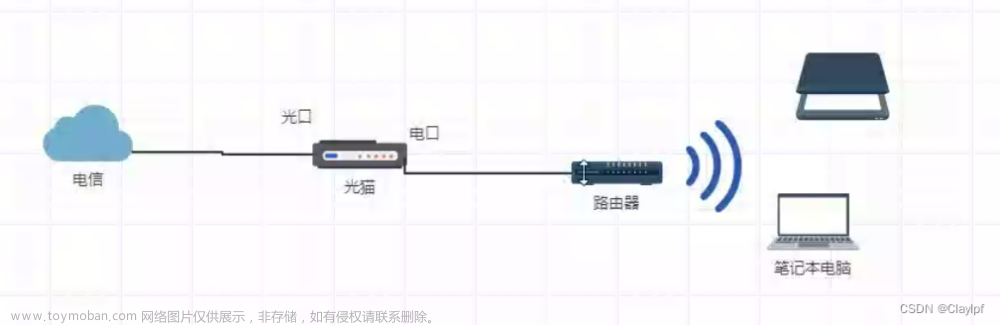
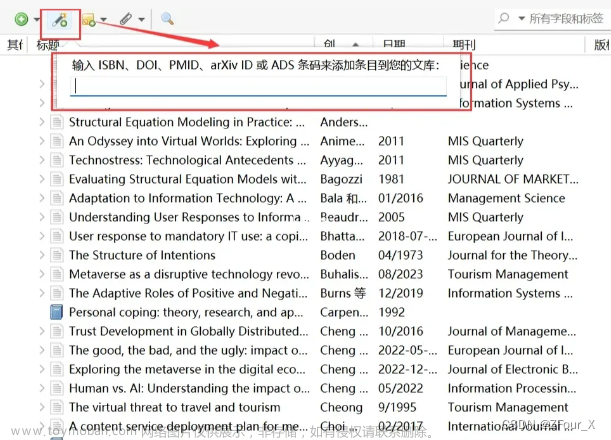
下图中，μ0 表示整个地区的总体均值，μ 表示整个矿区的整体均值， $\overline{X}$ 表示矿区抽样的均值

H0是无效假设(原假设)，即，矿区的均值和该地区的均值其实是一样的，只是因为抽样误差而导致的（即矿区的样本是整个地区样本的一部分）
H1是备择假设，即，矿区的数据分布和整个地区的数据分布是完全不同的，两者均值本身就不相等。所以从矿区中抽样出来的均值自然和整个地区的均值不同，即矿区影响了新生儿头围的发育

p 值计算（置信度）

如下图所示，S 表示标准差，n 表示样本数
p 值计算（置信度）

注意，这里需要对 μ 取绝对值，即 μ=2.273，2.273是介于 1.96 到 2.58 之间，所以 p 值介于 0.01 到 0.05 之间

μ 越大，p 越小；μ越小，p越大

接受 H1 即表示：矿区新生儿的头围，和全地区的数据，是不一致的

如下图所示，即表示，H0的零假设其实就是假设 “没有差别”，拒绝了 “没有差别” 的假设，那结论自然就是 “有差别”
p 值计算（置信度）

p 值计算（置信度）

参考：【统计】从P值到6σ（六西格玛）质量控制（P值与Z值，与置信水平的关系，python scipy 计算）

p 值计算（置信度）

下图中，z=1.96 表示，距离均值 1.96 个标准差
p 值计算（置信度）

In [88]: from scipy.stats import norm

In [89]: help
Out[89]: Type help() for interactive help, or help(object) for help about object.

In [90]: help(norm.cdf)


In [91]: norm.cdf(1.96)
Out[91]: 0.9750021048517795

In [92]: norm.cdf(-1.96)
Out[92]: 0.024997895148220435

In [93]: norm.cdf(1.96)-norm.cdf(-1.96)
Out[93]: 0.950004209703559


# 参考 https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.t.html
# sf = 1 - cdf
# 注意下面的参数 df 表示自由度
In [113]: 1-scipy.stats.t.sf(1.67, df=1)
Out[113]: 0.8282595795437305

In [114]: scipy.stats.t.cdf(1.67, df=1)
Out[114]: 0.8282595795437305

二、T检验

参考：

(知乎) 一文详解t检验 ⭐️⭐️⭐️⭐️⭐️)
(知乎) t检验自由度如何选择？⭐️⭐️⭐️

关于两个样本均值之差的分布：

p 值计算（置信度）

参考：

T检验、T分布、T检验的计算方法

如下图，T分布的自由度 df 越大，则越趋近于正态分布
p 值计算（置信度）

三、实际计算

在做AB实验时，经常需要计算实验的p值，当p<0.05时，表示该实验的结论是置信的（原假设是实验组和基线没有差别，备择假设是实验组和基线有差别，当p<0.05时，即接受备择假设，即表示实验组和基线有区别）

""" 
t 检验, T 检验用于确定两个变量的均值之间是否存在显著差异，并判断它们是否属于同一分布。
"""
from scipy.stats import t  


def adv_test(self, num_base, mu_base, var_base, num_exp, mu_exp, var_exp, alpha=0.05, beta=0.8):
	"""
	官方文档 https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.t.html
	exp 后缀表示实验组，base 后缀表示基线组
	"""
    num = num_exp + num_base
    mu = mu_exp - mu_base
    mu_ratio = float(mu_exp)/float(mu_base)-1
    # print("mu_exp: {}, mu_base: {}".format(mu_exp, mu_base))
    var = var_exp / num_exp + var_base / num_base
    t_value = mu / np.sqrt(var)

    # 自由度 degrees of freedom，当自由度足够大时，计算出来的p值几乎没有差别
    df = num - 1
    # df = var**2 / ((var_exp**2)/(num_exp**2 * (num_exp-1)) + (var_base**2) / (num_base**2 * (num_base-1)))
    print("mu: {}, var: {}, t_value: {}, df: {}".format(mu, var, t_value, df))
    # 这里 t.sf = 1-t.cdf，t.sf 的第二个参数是 df，即自由度(df, degrees of freedom)
    pvalue = t.sf(t_value, df)
    half_alpha_percentile = t.isf(alpha / 2, df)
    lower_bound = mu - half_alpha_percentile * np.sqrt(var)
    upper_bound = mu + half_alpha_percentile * np.sqrt(var)
    mde = (t.isf(alpha / 2, num - 2) - t.isf(beta, num - 2)) * np.sqrt(var)
    # return pvalue, lower_bound, upper_bound, mu
    return pvalue, lower_bound, upper_bound, mu_ratio

"""
######### arpu 相对值 #######
# old_df，自由度 df=num-1
mu: 0.007, var: 0.00119234226134, t_value: 0.202720454552, df: 26764544
In [193]: 0.007 / np.sqrt(0.00119234226134)
Out[193]: 0.20272045455163987

In [179]: t.sf(0.202720454552, 26764544)
Out[179]: 0.4196767681194182


# new_df,自由度 df=var**2 / ((var_exp**2)/(num_exp**2 * (num_exp-1)) + (var_base**2) / (num_base**2 * (num_base-1)))
mu: -0.007, var: 0.00119234226134, t_value: -0.202720454552, df: 8170882.10005
In [180]: t.sf(0.202720454552, 8170882.10005)
Out[180]: 0.4196767698726953

######### arpu 绝对值 #######
# old_df,自由度 df=num-1
mu: 0.16, var: 0.624730231747, t_value: 0.2024294622, df: 26764544
In [194]: 0.16 / np.sqrt(0.624730231747)
Out[194]: 0.20242946219986416

In [190]: t.sf(0.2024294622, 26764544)
Out[190]: 0.41979049958805537


# new_df，自由度df=var**2 / ((var_exp**2)/(num_exp**2 * (num_exp-1)) + (var_base**2) / (num_base**2 * (num_base-1)))
mu: 0.16, var: 0.624730231747, t_value: 0.2024294622, df: 8170882.10005
In [191]: t.sf(0.2024294622, 8170882.1005)
Out[191]: 0.4197905013387206


#################### 结论 #####################
1. 使用arpu 绝对值 还是 相对值，计算出来的p值没有差异
2. 使用新版的 df 计算方法，p值也没有差异（当自由度足够大时，对p值计算几乎没有影响了，因为当自由度足够大时，已经趋近于正态分布，算出来的面积已经基本是不变的常数了）
"""

关于自由度 df 的理解

根据谢宇老师《回归分析》一书中的介绍：自由度是通过样本统计量来估计总体参数时必须涉及的一个基本概念，指的是计算样本统计量时能自由取值的数值个数。当做t检验时，是用样本方差去对总体方差进行估计。需要变量减去观测样本的均值，故而样本中只有n-1个自由取值。确定了n-1个数，基于均值，第n个数就确定了。所以一般来讲，丧失的自由度数目也就是需要估计的参数的数目，或者约束条件的数目。

其他参考文章来源地址https://www.toymoban.com/news/detail-482398.html