正定矩阵与可逆矩阵的关系-Toy模板网

这篇具有很好参考价值的文章主要介绍了正定矩阵与可逆矩阵的关系。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、矩阵可逆

1. 可逆定义：

在线性代数中，给定一个n阶方阵A，若存在一n阶方阵B使得AB=BA=E，其中E为n阶单位矩阵，则称A是可逆的，且B是A的可逆阵，记作A^-1

2. 可逆充要条件：

（1）AB=E（E为单位阵）；
（2）矩阵A满秩（即r(A)=n）；
（3）A的特征值全不为0；
（4）A的行列式|A|≠0，也可表述为A是非奇异矩阵（即行列式不为0的矩阵）；
（5）齐次线性方程组AX=0 仅有零解；
（6）非齐次线性方程组AX=b 有唯一解；
（7）A的行（列）向量组线性无关；
（8）任一n维向量可由A的行（列）向量组线性表示。
注：以上条件全部是等价的

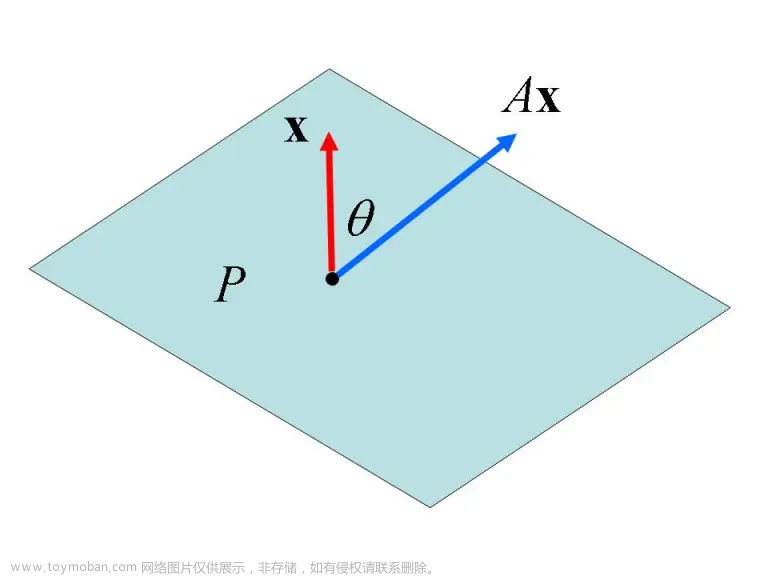
二、正定矩阵

1. 正定矩阵定义：

设M是n阶方阵，如果对任何非零向量z，都有z^TMz> 0，其中z^T 表示z的转置，就称M为正定矩阵。
其实，在线性代数中，正定矩阵的性质类似复数中的正实数

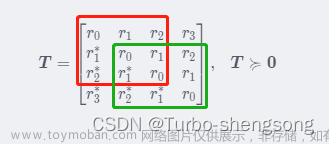
2. 正定矩阵性质：

（1）正定矩阵的行列式均大于0，且其一切顺序主子式均大于0；
（2）正定矩阵的逆矩阵也是正定矩阵；
（3）两个正定矩阵的和是正定矩阵；
（4）正实数与正定矩阵的乘积是正定矩阵；
（5）正定矩阵的特征值均为正。

三、正定矩阵与可逆矩阵

1.正定矩阵，一定可逆

证明：
因为：“正定矩阵A的行列式均大于0，且其一切顺序主子式均大于0”，
所以：“矩阵A满秩，一定可逆”

2.举例

如矩阵Q和R分别在什么情况下能保证矩阵M=A^TQA+R可逆？
分析：若R是正定的、Q半正定，显然M是正定的，因为Q半正定保证A^TQA半正定，而R是正定的，所以M一定是正定的；
又或者R是半正定的，Q是正定的，此时若A满秩，那么A^TQA一定正定，而R是半正定的，所以所以M一定是正定的，所以矩阵M=A^TQA+R可逆。文章来源地址https://www.toymoban.com/news/detail-482426.html

到了这里，关于正定矩阵与可逆矩阵的关系的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！