1.无约束优化算法
在机器学习中的无约束优化算法中,除了梯度下降以外,还有最小二乘法,牛顿法和拟牛顿法。
1.1最小二乘法
最小二乘法是计算解析解,如果样本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。
1.2梯度下降法
梯度下降法是迭代求解,是如果样本量很大,用最小二乘法由于需要求一个超级大的逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。
1.3牛顿法/拟牛顿法
牛顿法/拟牛顿法也是迭代求解,不过梯度下降法是梯度求解,而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言,使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。
2.一阶梯度优化
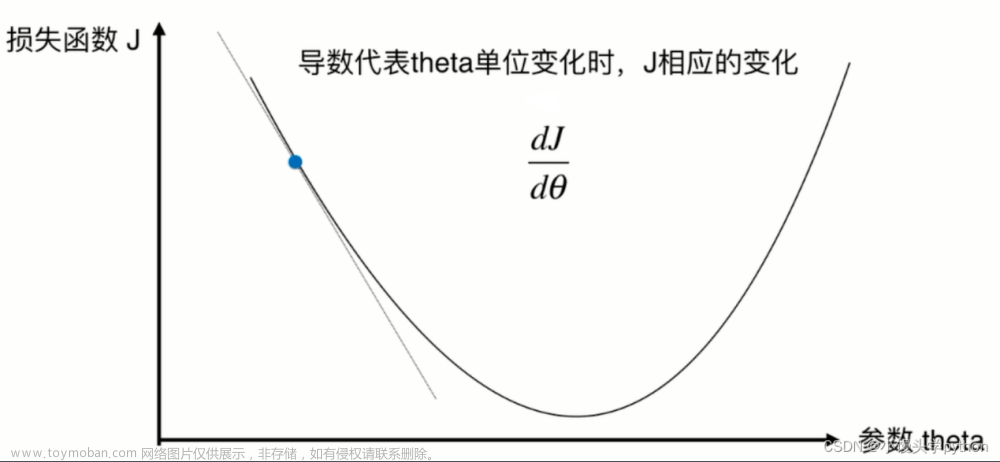
2.1梯度的数学原理
链接: 一文看懂常用的梯度下降算法
链接: 详解梯度下降法(干货篇)
链接: 梯度下降算法Gradient Descent的原理和实现步骤
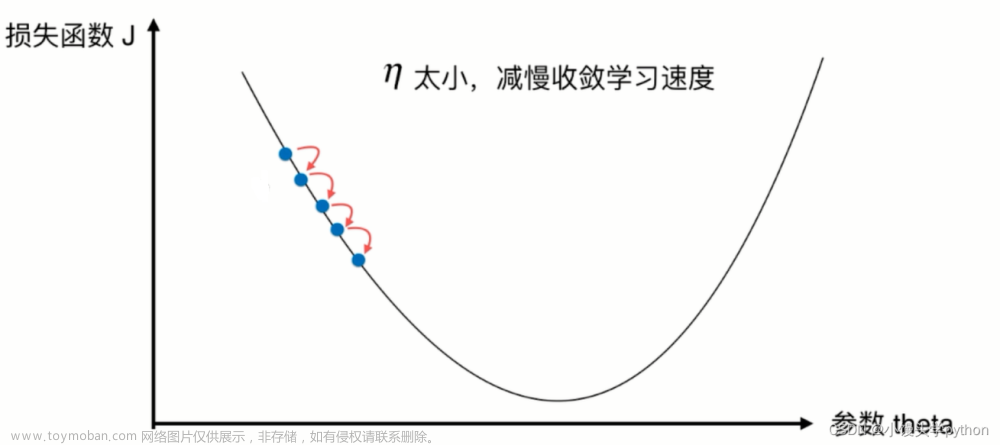
2.2梯度下降算法
链接: 梯度下降算法(附代码实现)
#定义函数
def f(x):
return 0.5 * (x - 0.25)**2
#f(x)的导数(现在只有一元所以是导数,如果是多元函数就是偏导数)
def df(x):
return x - 0.25 #求导应该不用解释吧
alpha = 1.8 #你可以更改学习率试试其他值
GD_X = [] #每次x更新后把值存在这个列表里面
GD_Y = [] #每次更新x后目标函数的值存在这个列表里面
x = 4 #随机初始化的x,其他的值也可以
f_current = f_change = f(x)
iter_num = 0
while iter_num <100 and f_change > 1e-10: #迭代次数小于100次或者函数变化小于1e-10次方时停止迭代
iter_num += 1
x = x - alpha * df(x)
tmp = f(x)
f_change = abs(f_current - tmp)
f_current = tmp
GD_X.append(x)
GD_Y.append(f_current)
import numpy as np
import matplotlib.pyplot as plt
X = np.arange(-4,4,0.05)
Y = f(X)
Y = np.array(Y)
plt.plot(X,Y)
plt.scatter(GD_X,GD_Y)
plt.title("$y = 0.5(x - 0.25)^2$")
plt.show()
plt.plot(X,Y)
plt.plot(GD_X,GD_Y) #注意为了显示清楚每次变化这里我做了调整
plt.title("$y = 0.5(x - 0.25)^2$")
plt.show()
3.二阶梯度优化梯度优化
3.1 牛顿法
3.2 拟牛顿法
拟牛顿算法是二阶梯度下降吗?
是的,拟牛顿算法是一种二阶梯度下降算法。它通过估计目标函数的海森矩阵的逆矩阵来近似实际的牛顿方法,以加快收敛速度。与传统的一阶梯度下降算法相比,拟牛顿算法具有更快的收敛速度和更好的收敛性能。
LBFGS是拟牛顿算法吗
是的,LBFGS(Limited-memory Broyden-Fletcher-Goldfarb-Shanno)是一种拟牛顿算法。它是一种基于梯度的优化算法,通过逐步近似目标函数的海森矩阵的逆矩阵来更新参数。LBFGS算法主要的特点是利用有限的内存来存储历史信息,从而避免了海森矩阵的存储和计算,同时具有较好的收敛性能和计算效率。LBFGS算法在实际应用中广泛使用,特别是对于大规模优化问题的求解,是一种非常有效的算法。
链接: 二阶优化方法——牛顿法、拟牛顿法(BFGS、L-BFGS)
链接: L-BFGS算法
链接: 【技术分享】L-BFGS算法
链接: 机器学习基础·L-BFGS算法
链接: 一文读懂L-BFGS算法
链接: PyTorch 学习笔记(七):PyTorch的十个优化器
链接: 二阶梯度优化新崛起,超越 Adam,Transformer 只需一半迭代量
链接: 神经网络的训练可以采用二阶优化方法吗?文章来源:https://www.toymoban.com/news/detail-482683.html
代码备份文章来源地址https://www.toymoban.com/news/detail-482683.html
#pytorch==1.8.1
#transformers==3.1.0
#tensorflow==2.4.1
#keras==2.4.3
import warnings
warnings.filterwarnings("ignore")
import time
import random
from sklearn.metrics import f1_score
import pandas as pd
import numpy as np
np.random.seed(2020)
from tqdm import tqdm,tqdm_notebook
import torch
from transformers import *
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(2020)
torch.cuda.manual_seed(2020)
torch.backends.cudnn.deterministic = True
import time
import warnings
import numpy as np
import pandas as pd
from mealpy.evolutionary_based.GA import BaseGA
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import statsmodels.api as sm
from scipy.stats import spearmanr
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
from plotnine import *
import torch
import torch.nn as nn
import torch.nn.functional as F
from numpy import abs as P
from numpy import square as squa
from numpy import sqrt as sqt
#from __functions__ import check
#from utils import residuals
warnings.filterwarnings('ignore')
def MAE(y_true, y_pred):
return mean_absolute_error(y_true, y_pred)
def RMSE(y_true, y_pred):
return np.sqrt(mean_squared_error(y_true, y_pred))
def MAPE(y_true, y_pred):
return 1.0/len(y_true) * np.sum(np.abs((y_pred-y_true)/y_true)) * 100
def SMAPE(y_true, y_pred):
return 1.0/len(y_true) * np.sum(np.abs(y_pred-y_true) / (np.abs(y_pred)+np.abs(y_true))/2) * 100
def CORR(y_true, y_pred):
return np.corrcoef(y_true, y_pred)[0][1]
def AIC(y_true, y_pred):
X = sm.add_constant(y_pred)
ols = sm.OLS(y_true, X)
ols_res = ols.fit()
return ols_res.aic
def BIC(y_true, y_pred):
X = sm.add_constant(y_pred)
ols = sm.OLS(y_true, X)
ols_res = ols.fit()
return ols_res.bic
def SpearmanR(y_true, y_pred):
tmp = spearmanr(y_true, y_pred)
return tmp.correlation
class CorrLoss(nn.Module):
def __init__(self):
super(CorrLoss,self).__init__()
def forward(self, input1, input2):
input1 = input1 - torch.mean(input1)
input2 = input2 - torch.mean(input2)
cos_sim = F.cosine_similarity(input1.view(1, -1), input2.view(1, -1))
return 1 - cos_sim
class AGBO(nn.Module):
def __init__(self):
super(AGBO, self).__init__()
self.R_d = torch.tensor(0.5, dtype=torch.float, requires_grad=True)
self.X_d = torch.tensor(0.5, dtype=torch.float, requires_grad=True)
self.G_d = torch.tensor(0.5, dtype=torch.float, requires_grad=True)
self.B_d = torch.tensor(0.5, dtype=torch.float, requires_grad=True)
self.R_cd = torch.tensor(0.5, dtype=torch.float, requires_grad=True)
self.X_cd = torch.tensor(0.5, dtype=torch.float, requires_grad=True)
self.lr_weight = torch.tensor(0.5, dtype=torch.float, requires_grad=True)
self.lr_bias = torch.tensor(0.5, dtype=torch.float, requires_grad=True)
self.__init_params__()
def forward(self, U_ld, P_ld, Q_ld):
# Delta_U_d 节点d处变压器阻抗电压降落的纵分量
Delta_U_d = (P_ld * torch.abs(self.R_d*9.2+0.8) + Q_ld * torch.abs(self.X_d*15+5)) / U_ld
# delta_U_d 节点d处变压器阻抗电压降落的横分量
delta_U_d = (P_ld * torch.abs(self.X_d*15+5) - Q_ld * torch.abs(self.R_d*9.2+0.8)) / U_ld
# P_d 节点d高压侧的有功功率
P_d = P_ld + (torch.pow(P_ld, 2) + torch.pow(Q_ld, 2)) / torch.pow(U_ld, 2) * torch.abs(self.R_d*9.2+0.8) + torch.pow(U_ld, 2) * torch.abs(self.G_d*4e-6+4e-6)
# Q_d 节点d高压侧的无功功率
Q_d = Q_ld + (torch.pow(P_ld, 2) + torch.pow(Q_ld, 2)) / torch.pow(U_ld, 2) * torch.abs(self.X_d*15+5) + torch.pow(U_ld, 2) * torch.abs(self.B_d*6e-5+2e-5)
# U_d 节点d高压侧的电压
U_d = torch.sqrt(torch.pow(U_ld+Delta_U_d, 2) + torch.pow(delta_U_d, 2))
# Delta_U_cd 支路a上电压降落的纵分量
Delta_U_cd = (P_d * torch.abs(self.R_cd*0.495+0.005) + Q_d * torch.abs(self.X_cd*0.495+0.005)) / U_d
# delta_U_cd 支路a上电压降落的横分量
delta_U_cd = (P_d * torch.abs(self.X_cd*0.495+0.005) - Q_d * torch.abs(self.R_cd*0.495+0.005)) / U_d
# Uc 节点c的电压
U_c_calc = torch.sqrt(torch.pow(U_d+Delta_U_cd, 2) + torch.pow(delta_U_cd, 2))
# outputs = U_c_calc
outputs = U_c_calc * (self.lr_weight*0.4+0.8) + (self.lr_bias*1000)
return outputs
def __init_params__(self):
nn.init.uniform_(self.R_d, 0, 1)
nn.init.uniform_(self.X_d, 0, 1)
nn.init.uniform_(self.G_d, 0, 1)
nn.init.uniform_(self.B_d, 0, 1)
nn.init.uniform_(self.R_cd, 0, 1)
nn.init.uniform_(self.X_cd, 0, 1)
nn.init.uniform_(self.lr_weight, 0, 1)
nn.init.uniform_(self.lr_bias, 0, 1)
rawdata = pd.read_csv('v20210306.csv')
DEVICE = 'cpu'
train_data, test_data = train_test_split(rawdata, test_size=0.25, shuffle=True, random_state=2022)
U_ld_train, U_ld_test = train_data['A相电压值L'].values, test_data['A相电压值L'].values
P_ld_train, P_ld_test = train_data['A相有功'].values, test_data['A相有功'].values
Q_ld_train, Q_ld_test = train_data['A相无功'].values, test_data['A相无功'].values
U_c_train, U_c_test = train_data['A相电压值H'].values, test_data['A相电压值H'].values
U_ld_train, U_ld_test = U_ld_train * 10 / 0.38, U_ld_test * 10 / 0.38
U_ld_train_tensor, U_ld_test_tensor = torch.tensor(U_ld_train, dtype=torch.float), torch.tensor(U_ld_test, dtype=torch.float)
P_ld_train_tensor, P_ld_test_tensor = torch.tensor(P_ld_train, dtype=torch.float), torch.tensor(P_ld_test, dtype=torch.float)
Q_ld_train_tensor, Q_ld_test_tensor = torch.tensor(Q_ld_train, dtype=torch.float), torch.tensor(Q_ld_test, dtype=torch.float)
U_c_train_tensor, U_c_test_tensor = torch.tensor(U_c_train, dtype=torch.float), torch.tensor(U_c_test, dtype=torch.float)
U_ld_train_tensor, U_ld_test_tensor = U_ld_train_tensor.to(DEVICE), U_ld_test_tensor.to(DEVICE)
P_ld_train_tensor, P_ld_test_tensor = P_ld_train_tensor.to(DEVICE), P_ld_test_tensor.to(DEVICE)
Q_ld_train_tensor, Q_ld_test_tensor = Q_ld_train_tensor.to(DEVICE), Q_ld_test_tensor.to(DEVICE)
U_c_train_tensor, U_c_test_tensor = U_c_train_tensor.to(DEVICE), U_c_test_tensor.to(DEVICE)
model = AGBO()
model = model.to(DEVICE)
epochs = 1000
lr = 5e-3
weight_decay = 1e-6
optimizer = torch.optim.LBFGS([model.R_d, model.X_d, model.G_d, model.B_d, model.R_cd, model.X_cd],
lr=lr)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=2)
loss_fn = nn.MSELoss()
def closure():
optimizer.zero_grad()
loss = loss_fn(model(U_ld_train_tensor,P_ld_train_tensor,Q_ld_train_tensor), U_c_train_tensor)
loss.backward()
return loss
all_train_loss, all_test_loss = [], []
for epoch in range(epochs):
model.train()
optimizer.zero_grad()
outputs = model(U_ld_train_tensor, P_ld_train_tensor, Q_ld_train_tensor)
train_loss = loss_fn(outputs, U_c_train_tensor)
train_loss.backward()
optimizer.step(closure)
scheduler.step(train_loss)
# setting optimazing bound
model.R_d.data = model.R_d.clamp(0, 1).data
model.X_d.data = model.X_d.clamp(0, 1).data
model.G_d.data = model.G_d.clamp(0, 1).data
model.B_d.data = model.B_d.clamp(0, 1).data
model.R_cd.data = model.R_cd.clamp(0, 1).data
model.X_cd.data = model.X_cd.clamp(0, 1).data
model.lr_weight.data = model.R_cd.clamp(0, 1).data
model.lr_bias.data = model.R_cd.clamp(0, 1).data
with torch.no_grad():
model.eval()
outputs_test = model(U_ld_test_tensor, P_ld_test_tensor, Q_ld_test_tensor)
test_loss = loss_fn(outputs_test, U_c_test_tensor)
all_train_loss.append(float(train_loss.detach().cpu().numpy()))
all_test_loss.append(float(test_loss.detach().cpu().numpy()))
# verbose
if epoch%50 == 0:
#print('the epoch is %d with train loss of %f' %(epoch, train_loss.detach().cpu().numpy()))
print('the epoch is %d with test loss of %f' %(epoch, test_loss.detach().cpu().numpy()))
model.eval()
outputs_train = model(U_ld_train_tensor, P_ld_train_tensor, Q_ld_train_tensor)
outputs_test = model(U_ld_test_tensor, P_ld_test_tensor, Q_ld_test_tensor)
lr = LinearRegression()
lr.fit(outputs_train.detach().cpu().numpy().reshape(-1, 1), train_data['A相电压值H'].values.reshape(-1, 1))
outputs_train = lr.predict(outputs_train.detach().cpu().numpy().reshape(-1, 1))
outputs_test = lr.predict(outputs_test.detach().cpu().numpy().reshape(-1, 1))
plt.figure(figsize=(8, 6))
plt.plot(train_data['A相电压值H'], outputs_train, 'ok')
plt.plot(test_data['A相电压值H'], outputs_test, '^r')
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
plt.xlabel('Uc', fontdict={'family':'Times new Roman', 'size':24})
plt.ylabel('Ucal', fontdict={'family':'Times new Roman', 'size':24})
plt.legend(['train sample', 'test_sample'])
plt.savefig('agbo-nonlr-45.tiff', dpi=150)
print(np.corrcoef(test_data['A相电压值H'], outputs_test.ravel()))
print('+++ test results +++')
print(MAE(test_data['A相电压值H'], outputs_test))
print(RMSE(test_data['A相电压值H'], outputs_test))
print(MAPE(test_data['A相电压值H'], outputs_test.ravel()))
print(SMAPE(test_data['A相电压值H'], outputs_test.ravel()))
到了这里,关于梯度下降优化的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!