基于EasyX学习图形学中的三维几何变换【全】-Toy模板网

这篇具有很好参考价值的文章主要介绍了基于EasyX学习图形学中的三维几何变换【全】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言

本文开始学习几何变换中的三维变换，对于各种变换的定义方法基本和二维变换一样，在此我就不过多赘述了。
三维变换矩阵
由于二维变换矩阵为三阶矩阵，所以三维变换矩阵为四阶矩阵
以下例子均在此正方体基础上

一、平移变换

坐标表示
矩阵表示
变换矩阵

#include "E_Point3.h"
class E_Transform3
{
public:
	double T[4][4];
	E_Point3* P;
	int PtrNum;
public:
	~E_Transform3() {}
	E_Transform3(){}

	void SetMatrix(E_Point3* P, int Pt);//获取顶点表和顶点个数
	void E_Translate(double tx, double ty, double tz);//平移函数

	void E_RotateX(double thet);//X轴旋转函数
	void E_RotateY(double thet);//Y轴旋转函数
	void E_RotateZ(double thet);//Z轴旋转函数
	void E_RotatePX(double thet, E_Point3 P);//绕点旋转函数
	void E_RotatePY(double thet, E_Point3 P);//绕点旋转函数
	void E_RotatePZ(double thet, E_Point3 P);//绕点旋转函数
	void E_RotatePXY(double thet, E_Point3 P);//绕点旋转函数

	void E_Scale(double dx, double dy, double dz);//缩放函数

	void E_ReflectZ();//Z轴反射
	void E_ReflectX();//X轴反射
	void E_ReflectY();//Y轴反射

	void E_ReflectZOX();//ZOX面反射
	void E_ReflectXOY();//XOY面反射
	void E_ReflectYOZ();//YOZ面反射

	void E_ShearX(double b, double c);//沿X方向错切变换
	void E_ShearY(double b, double c);//沿Y方向错切变换
	void E_ShearZ(double b, double c);//沿Z方向错切变换

	void Identity();//对变换矩阵进行单位化
	void MultiplyMatrix();//进行矩阵乘法
};
#include "E_Point3.h"
#include "E_Facet.h"
#include "E_Point.h"
#include<graphics.h>
class E_Cube
{
public:
	E_Cube(){}
	~E_Cube() {}
	void GetPoint();//获取正方体各顶点坐标
	void GetFacet();//根据面将顶点排序
	E_Point3* GetVertexArrayName();//返回顶点数组
	void Draw();//绘制正方体
private:
	E_Point3 P[8];//八个顶点
	E_Facet F[6];//六个面
};

核心代码

void E_Transform3::SetMatrix(E_Point3* P, int Pt)
{
	this->P = P;
	this->PtrNum = Pt;
}

void E_Transform3::E_Translate(double tx, double ty, double tz)
{
	Identity();
	T[0][3] = tx; T[1][3] = ty; T[2][3] = tz;
	MultiplyMatrix();
}
///这是画正方体的函数
void E_Cube::Draw()
{
	E_Point ScreenPoint, temp;
	for (int nFacet = 0; nFacet < 6; nFacet++) {
		for (int nPoint = 0; nPoint < 4; nPoint++) {
			/*
			获取每个面上的点
			由于是直接投影到xoy平面所以本次投影为正交投影
			F[nFacet].Index[nPoint]表示每个面上的点的索引
			*/
			ScreenPoint.x = P[F[nFacet].Index[nPoint]].x;
			ScreenPoint.y = P[F[nFacet].Index[nPoint]].y;
			if (0 == nPoint) {//获取每个面的起始点
				moveto(ScreenPoint.x, ScreenPoint.y);
				temp = ScreenPoint;
			}
			else {
				lineto(ScreenPoint.x, ScreenPoint.y);
			}
		}
		lineto(temp.x, temp.y);//最后闭合四边形
	}
}
主函数
	HWND hwnd = initgraph(500, 500);
	setorigin(250, 250);
	setaspectratio(1, -1);
	setbkcolor(WHITE);
	cleardevice();
	setlinecolor(BLACK);
	setlinestyle(PS_SOLID, 2);
	E_Cube Cube;
	E_Transform3 Translate;
	Cube.GetPoint();
	Cube.GetFacet();
	for (; 1;) {
		Cube.Draw();
		Sleep(500);
		cleardevice();
		Translate.SetMatrix(Cube.GetVertexArrayName(), 8);
		Translate.E_Translate(2,0,0);//沿x方向平移
	}
	closegraph();
	return 0;

效果展示

二、比例变换

坐标表示
矩阵表示
变换矩阵
核心代码文章来源地址https://www.toymoban.com/news/detail-483846.html

void E_Transform3::E_Scale(double dx, double dy, double dz)
{
	Identity();
	T[0][0] = dx; T[1][1] = dy; T[2][2] = dz;
	MultiplyMatrix();
}
///主函数
	HWND hwnd = initgraph(500, 500);
	setorigin(250, 250);
	setaspectratio(1, -1);
	setbkcolor(WHITE);
	cleardevice();
	setlinecolor(BLACK);
	setlinestyle(PS_SOLID, 2);
	E_Cube Cube;
	E_Transform3 Scale;
	Cube.GetPoint();
	Cube.GetFacet();
	for (; 1;) {
		Cube.Draw();
		Sleep(1000);
		cleardevice();
		Scale.SetMatrix(Cube.GetVertexArrayName(), 8);
		Scale.E_Scale(1.1,1.1,1.1);//正方体放大1.1倍
	}
	closegraph();
	return 0;

效果展示

三、旋转变换

坐标表示

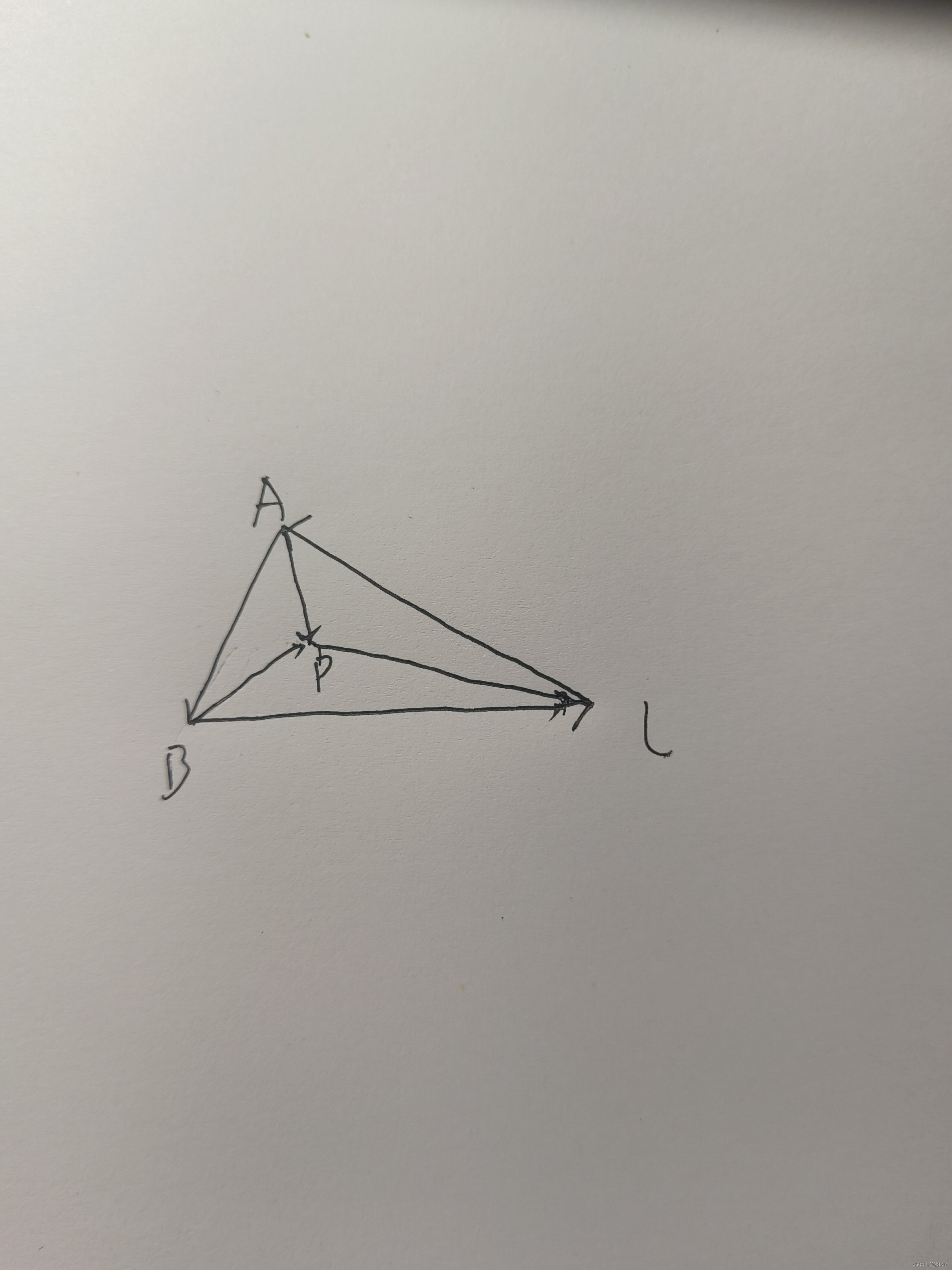
在此我从二维旋转推一下三维坐标旋转变换

基于EasyX学习图形学中的三维几何变换【全】
从此图可以得出二维旋转变换的一系列表示

基于EasyX学习图形学中的三维几何变换【全】

在此基础上加一个z轴旋转并没有发生什么改变，则此二维旋转便可以看作是绕z轴旋转，则可以得出三维旋转中的绕z轴旋转

基于EasyX学习图形学中的三维几何变换【全】

从绕z轴的旋转变换便可以得出绕其它轴的变换，原理很简单，将x,y,z的位置交换但要符合右手坐标系，再来推一个绕y轴变换的

基于EasyX学习图形学中的三维几何变换【全】

同理便可得出绕x轴旋转的坐标表示

矩阵表示
根据坐标表示便可得出矩阵表示，在此列出绕z轴的矩阵表示
变换矩阵
此处只列出绕z轴旋转的变换矩阵
核心代码

void E_Transform3::E_RotateX(double thet)
{
	Identity();
	T[1][1] = cos(thet); T[1][2] = -sin(thet); T[2][1] = sin(thet); T[2][2] = cos(thet);
	MultiplyMatrix();
}

void E_Transform3::E_RotateY(double thet)
{
	Identity();
	T[0][0] = cos(thet); T[2][0] = -sin(thet); T[0][2] = sin(thet); T[2][2] = cos(thet);
	MultiplyMatrix();
}

void E_Transform3::E_RotateZ(double thet)
{
	Identity();
	T[0][0] = cos(thet); T[0][1] = -sin(thet); T[1][0] = sin(thet); T[1][1] = cos(thet);
	MultiplyMatrix();
}
///主函数
#include "E_Cube.h"
#include "E_Transform3.h"
#define PI 3.1415926
int main() {
	HWND hwnd = initgraph(500, 500);
	setorigin(250, 250);
	setaspectratio(1, -1);
	setbkcolor(WHITE);
	cleardevice();
	setlinecolor(BLACK);
	setlinestyle(PS_SOLID, 2);
	E_Cube Cube;
	E_Transform3 Rotate;
	Cube.GetPoint();
	Cube.GetFacet();
	for (; 1;) {
		Cube.Draw();
		Sleep(1000);
		cleardevice();
		
		Rotate.SetMatrix(Cube.GetVertexArrayName(), 8);
		Rotate.E_RotateZ(PI / 6);
		Rotate.E_RotateY(PI / 6);
		Rotate.E_RotateX(PI / 6);
	}
	closegraph();
	return 0;
}

效果展示

四、反射变换

坐标表示
- 以下依次为x轴、y轴、z轴的反射
- 以下依次为xoy面、zox面、yoz面反射
矩阵表示
这里只以x轴反射为例
变换矩阵
这里只以x轴反射为例
核心代码

void E_Transform3::E_ReflectZ()//z轴
{
	Identity();
	T[0][0] = -1; T[1][1] = -1; T[2][2] = 1;
	MultiplyMatrix();
}

void E_Transform3::E_ReflectX()//x轴
{
	Identity();
	T[0][0] = 1; T[1][1] = -1; T[2][2] = -1;
	MultiplyMatrix();
}

void E_Transform3::E_ReflectY()//y轴
{
	Identity();
	T[0][0] = -1; T[1][1] = 1; T[2][2] = -1;
	MultiplyMatrix();
}

void E_Transform3::E_ReflectZOX()//zox面
{
	Identity();
	T[0][0] = 1; T[1][1] = -1; T[2][2] = 1;
	MultiplyMatrix();
}

void E_Transform3::E_ReflectXOY()//xoy面
{
	Identity();
	T[0][0] = 1; T[1][1] = 1; T[2][2] = -1;
	MultiplyMatrix();
}

void E_Transform3::E_ReflectYOZ()//yoz面
{
	Identity();
	T[0][0] = -1; T[1][1] = 1; T[2][2] = 1;
	MultiplyMatrix();
}

五、错切变换

坐标表示
矩阵表示
变换矩阵
核心代码

void E_Transform3::E_ShearX(double b, double c)
{
	Identity();
	T[0][2] = b; T[0][3] = c; 
	MultiplyMatrix();
}

void E_Transform3::E_ShearY(double b, double c)
{
	Identity();
	T[1][0] = b; T[1][3] = c;
	MultiplyMatrix();
}

void E_Transform3::E_ShearZ(double b, double c)
{
	Identity();
	T[2][0] = b; T[2][1] = c;
	MultiplyMatrix();
}