C++【实现AVL树】-Toy模板网

这篇具有很好参考价值的文章主要介绍了C++【实现AVL树】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、AVL树的概念及性能

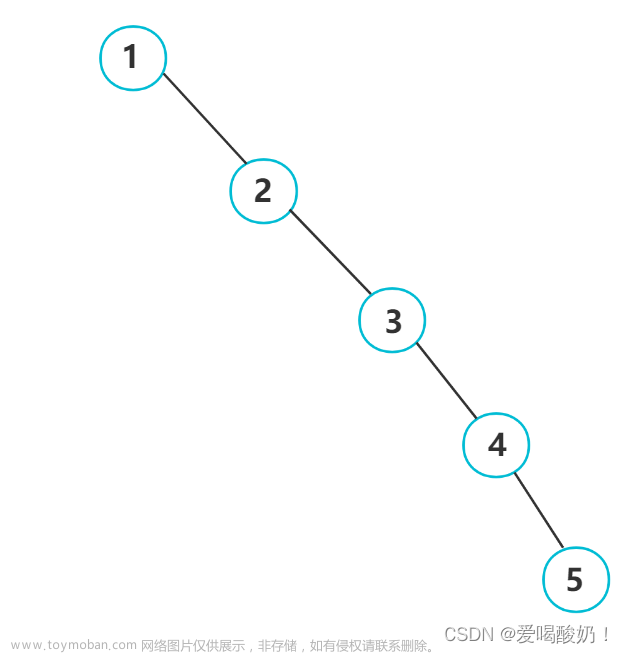
背景：我们所使用的的二叉搜索树虽然可以提高查找的效率，但如果有序或者接近有序的时候，二叉搜索树会变成一颗单支树，高度一边很高，另一边很低，时间复杂度变为O(n)，效率变低。
而AVL树的出现就是解决以上的问题的，当向二叉搜索树中插入新结点后，能保证每个结点的左右子树高度之差的绝对值不超过1，即可降低树的高度，减少搜索次数。
概念：AVL 树是一种平衡二叉搜索树，它的特点是每个节点的左右子树的高度差不超过1而且它的左右子树都是AVL树。
性能：AVL树这样可以保证查询时高效的时间复杂度，即O(log n)。但是不要对AVL树做一些结构修改的操作，效率会变低，比如删除：因为删除节点后的平衡因子需要更新，最差情况下要调整到根节点的位置；还有插入时要维持平衡，旋转的次数过多。所以如果数据结构不经常修改而且查询有序数据(基本不发生变化)的时候可以选择AVL树。

二、AVL树结点的创建

#pragma once
template<class K,class V>
class AVLTreeNode
{
	AVLTreeNode* left;
	AVLTreeNode* right;
	AVLTreeNode* parent;
	std::pair<K, V>_kv;
	int _bf;
	AVLTreeNode(const pair<K,V>&kv)
		:left(nullptr)
		,right(nullptr)
		,parent(nullptr)
		，_kv(kv)
		,_bf(0)
	{}
};
template<class K,class V>
class AVLTRee
{
	typedef AVLTreeNode<K, V> Node;
public:

private:
	Node* _root = nullptr;

};

三、AVL树的插入

bool Insert(const std::pair<K,V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
			   return false; 
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first > kv.first)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_parent = parent;

		while (parent)
		{
			if (cur ==parent->_right)
			{
				parent->_bf++;
			}
			else
			{
				parent->_bf--;
			}

			if (parent->_bf == 1 || parent->_bf == -1)
			{
				parent = parent->_parent;//继续更
				cur = cur->_parent;
			}
			else if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					RotateL(parent);//左单旋
				}
				else if (parent->_bf == -2 && cur->_bf == -1)
				{
					RotateR(parent);/右单旋
				}
				else if (parent->_bf == -2 && cur->_bf== 1)
				{
					RotateLR(parent);//左右旋
				}
				else if(parent->_bf==2&&cur->_bf==-1)
				{
				   RotateRL(parent);//右左旋
				}
				else
				{
					assert(false);
				}
				break;
			}
			else
			{
				assert(false);
			}
		}
		return true;
	}

AVL树首先是一个搜索树，它进行插入的时候就是完成搜索树的插入。

pair不是C++的内置类型，它是一个标准库中的模板类型，需要包含相应头文件进行声明。要正确使用pair，需要在文件开头添加头文件，我们使用了std::pair代替了局部定义的pair，同时在文件开头包含了头文件。这样，编译器就会知道std::pair是一个合法的类型，可以正确编译代码。

插入的值比你大往右边走，插入的值比小往左边走，相等直接false。
然后走完while再链接，申请新节点，这里需要判断父结点和当前结点的大小以确定插入的位置，比父小插左边，比父大插右边，再反向链接父结点。

搜索树插入完成，进行AVL树，接下来就是更新平衡因子。影响一个结点的平衡因子的因素是左右子树的高度，那新增的结点的bf一定是0，怎么衡量一颗树有没有受到影响，有没有出问题处理一下，就是更新bf，如果bf没有出现问题说明树的平衡没有受到影响即|bf|<=1,就不要处理，如果更新完成以后，平衡出现问题即|bf|>1,平衡结构受到影响，需要处理就是要旋转。
插入新增结点会影响部分祖先或全部祖先的bf。
如何进行更新？
如果新增结点在父亲的右边，那父亲结点的右树-左树，平衡因子++
如果新增结点在父亲的左边，那父亲结点的右树-左树，平衡因子–

要不要再继续往上更新取决于更新完一遍之后父亲的bf怎么办，这时候分四种情况：
1.如果更新完之后父亲的bf变成1或-1：首先先想一下什么决定了要不要往上更新，是parent所在的高度变了往上更新，高度不变不更新。如果是1或-1，父亲所在的高度变了，因为插入之后变成1或-1，说明之前是0，左右两边高度相等，现在变成1或-1说明有一边高1，但绝对不是2，因为插入之前是一棵AVL树。
2.如果父亲结点的bf变成0：就不要往上更新，所子树高度不变，因为插入前的bf是1或-1，插入前一边高一边低，相当于此时把矮的那一边填上
3.父亲的平衡因子变成2或-2：子树的高度虽然变了，这时候就不需要更新，因为自己都不平衡了，先解决自己此时的问题，而1或-1还是可以接受的毕竟满足<=1。
怎么处理这棵子树，就是要旋转而旋转又分为四种情况：
左单旋
右单旋
左右旋
右左旋
最后做一下断言
在这里面旋转就是降低高度，结束之后就break。
4.加个断言，如果大于2的时候，就在这断住，说明插入的时候就出问题。

四、四种旋转

（1）LL-左单旋

C++【实现AVL树】

观察以上抽象图：
(抽象图表示的是有无数多种情况，h可以等0、1、2…)
对于上面的抽象图中的a,b,c的位置任意插入一个结点都会引发11所在结点的bf变成2，22所在结点的bf变成1，最终了为了实现降低高度，会引发左旋转。
为什么这么旋转？
因为旋转的原则是保持它继续为搜索树，旋转的目的使其左右均衡，降低树的高度。
详细解释：
上图在插入前，AVL树是平衡的，新节点插入到22的右子树中，22的右子树增加了一层，导致以11为根的二叉树不平衡，要让11平衡，只能将11右子树的高度减少一层，左子树增加一层，即将右子树往上提。这样11转下来，因为11比22小，只能将其放在22的左子树；而如果22有左子树，左子树的值一定小于22，大于11，只能将其放在11右子树，旋转完成后，更新节点的平衡因子即可。在旋转过程中，有以下几种情况需要考虑：
1.22节点的左孩子可能存在，也可能不存在。
2. 11可能是根节点，也可能是子树，如果是根节点，旋转完成后，要更新根节点，如果是子树，可能是某个节点的左子树，也可能是右子树。
总结：b变成了11的右子树，11变成22的左子树，22变成了根。
代码分析如下：

void RotateL(Node* parent)//左单旋
	{
		Node* suR = parent->_right;//11的右孩子即22
		Node* suRL = suR->_left;//11的右孩子的左孩子即b

		parent->_right = suRL;//11右孩子链接b
		if(suRL)//如果b不为空
		  suRL->_parent = parent;//更新双亲结点

	
		suR->_left=parent;//22上提，左孩子链接11
		parent->_parent = suR;//更新双亲结点
		
		Node* ppnode = parent->_parent;//维护父结点的父结点


		if (ppnode == nullptr)
		{
			suR = _root;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = suR;
			}
			else
			{
				ppnode->_right = suR;
			}
			suR->_parent = ppnode;
		}
		parent->_bf = suR->_bf = 0;//更新平衡因子

	}

1.维护两个结点11和22，先把11的左孩子和22的左孩子即b链接，再更新其父亲结点，因为b可能为空，所以在这加判断条件；
2.再把22往上提，它的左孩子和11链接，并更新其父亲结点；
3.但是父亲结点11可能是局部子树，也有可能是整颗树，还得需要判断parent上的结点，维护父结点的父节点。如果ppnode是空，说明是根，只有根结点没有父亲。如果是空的，让22做根节点，并让其父节点指向空，如果不为空，说明是局部子树，在这里还需要判断父结点11是其双亲的左子树还是右子树，如果是左子树，就把双亲的左子树和22链接，反之把双亲的右子树和22链接。再更新22的父亲节点。
4.最后更新部分结点的平衡因子。

（2）RR-右单旋

C++【实现AVL树】
观察以上抽象图：
对于上面的抽象图中的a,b,c的位置任意插入一个结点都会引发11所在结点的bf变成-1，22所在结点的bf变成-2，最终了为了实现降低高度，会引发右旋转。
为什么这么旋转？
保持它继续为搜索树，使其左右均衡，降低树的高度。
详细解释：
上图在插入前，AVL树是平衡的，新节点插入到11的左子树中，11的左子树增加了一层，导致以22为根的二叉树不平衡，要让22平衡，只能将22左子树的高度减少一层，右子树增加一层，即将左子树往上提。这样22转下来，因为22比11大，只能将其放在11的右子树；而如果11有右子树，右子树的值一定小于22，大于11，只能将其放在22的左子树，旋转完成后，更新节点的平衡因子即可。在旋转过程中，有以下几种情况需要考虑：
1.11节点的右孩子可能存在，也可能不存在。
2. 22可能是根节点，也可能是子树，如果是根节点，旋转完成后，要更新根节点，如果是子树，可能是某个节点的左子树，也可能是右子树。
总结：b变成了22的左子树，22变成11的右子树，11变成了根。
代码分析如下：

void RotateR(Node* parent)//右单旋
	{
		Node* suL = parent->_left;
		Node* suLR = suL->_right;

		parent->_left = suLR;
		if (suLR)
			suLR->_parent = parent;
			
		Node* ppnode = parent->_parent;
		suL->_right = parent;
		parent->_parent = suL;

		if (ppnode == nullptr)
		{
			_root = suL;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = suL;
			}
			else
			{
				ppnode->_right = suL;
			}
			suL->_parent = ppnode;
		}
		suL->_bf = parent->_bf = 0;
	}

1.维护两个结点11和22，先把11往上提，它的右孩子和22链接，并更新其父亲结点；
2.再把22的左孩子和11的右孩子即b链接，再更新其父亲结点，因为b可能为空，所以在这加判断条件；
3.但是父亲结点22可能是局部子树，也有可能是整颗树，还得需要判断parent上的结点，维护父结点的父节点。如果ppnode是空，说明是根，只有根结点没有父亲。如果是空的，让11做根节点，并让其父节点指向空，如果不为空，说明是局部子树，在这里还需要判断父结点22是其双亲的左子树还是右子树，如果是左子树，就把双亲的左子树和11链接，反之把双亲的右子树和11链接。再更新11的父亲节点。
4.最后更新部分结点的平衡因子。

（3）LR-左右旋

C++【实现AVL树】
观察上面抽象图：
(抽象图表示的是有无数多种情况，h可以等0、1、2…)
在b和c位置进行插入结点会引发两次旋转，左单旋和右单旋，而在d位置插入不会引发旋转，在a位置插入就变成了右单旋，所以同时触发左右旋的条件就是在b和c位置进行插入。
详细解释：
在6的左子树进行插入新节点后，6的左子树增加了一层，导致以根为9的二叉树不平衡，想要解决不平衡，需降低高度，要从下往上降高度：首先只看以根为3的二叉树实际上看看成左单旋，因为整体上看3的右子树增加了一层，需降低右子树高度，增加左子树高度，所以执行左单旋；执行完之后，可以看到以根为9的二叉树的左子树明显比右子树高，需要降低左子树高度，增加右子树高度，所以进行右单旋。
还有最后一步就是平衡因子的调节：如下图
C++【实现AVL树】

在b和c插入结点之后，可以看到3,6,9的平衡因子不同，还有一种情况h=0时，6就是新增，这时候平衡因子都为0。现在最重要的就是如何识别是在b插还是c插入，我们可以在左右单旋之前记录下suLR即6的平衡因子，如果bf等于1，说明是在c插入，如果bf等于-1说明是在b插入。然后就是bf等于0，平衡因子全都是0。
总结：左右旋就是把6提了上去，让6做了根，3和9做了6的左和右。
代码分析如下：

void RotateLR(Node* parent)//左右旋
	{
		Node* suL = parent->_left;
		Node* suLR = suL->_right;
		int bf = suLR->_bf;
		RotateL(parent->_left);
		RotateR(parent);
		if (bf == -1)//在b插入
		{
			parent->_bf = 1;
			suLR->_bf = 0;
			suL->_bf = 0;
		}
		else if (bf == 1)//在c插入
		{
			parent->_bf = 0;
			suLR->_bf = 0;
			suL->_bf = -1;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			suLR->_bf = 0;
			suL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

看图写代码：
C++【实现AVL树】

1.首先就要维护parent的左孩子suL，以及suL的右孩子，
2.为了方便判断在哪插入，再维护一个bf变量记录没插入suLR的平衡因子，
3.再进行左单旋和右单旋。
4.最后判断bf等于0的时候可以不写，但是在这建议要写上，如果没有进行单旋就麻烦了，所以不要依赖单旋，正好和最后的断言也区分开，万一不是三种情况，在这断住,可以帮助我们检查出问题。

（4）RL-右左旋

C++【实现AVL树】
观察上面抽象图：
b和c的四个孩子任意一个位置新增节点都引发旋转，这里是在c处新增，只是其中的一种情况，引发了两次旋转，右单旋和左单旋，而在a位置不会引发旋转，在d位置变成了左单旋，所以同时触发右左单旋的条件是在b和c位置进行插入。
详细解释:
在6的右子树进行插入新节点后，6的右子树增加了一层，导致以根为3的二叉树不平衡，想要解决不平衡，需降低高度，要从下往上降高度：首先只看以根为9的二叉树实际上可以看成右单旋，因为整体上看9的左子树增加了一层，需降低左子树高度，增加右子树高度，所以执行右单旋；执行完之后，可以看到以根为9的二叉树的右子树明显比左子树高，需要降低右子树高度，增加左子树高度，所以进行左单旋。
还有最后一步就是平衡因子的调节：如下图
C++【实现AVL树】
在b和c插入结点之后，可以看到3,6,9的平衡因子不同，还有一种情况h=0时，6就是新增，这时候平衡因子都为0。如何识别是在b插还是c插入，我们可以在右左单旋之前记录下suRL即6的平衡因子，如果bf等于-1，说明是在b插入，如果bf等于1说明是在c插入。然后就是bf等于0，平衡因子全都是0。
代码分析如下：
C++【实现AVL树】
代码分析如下：

void RotateRL(Node* parent)//右左旋
	{
		Node* suR = parent->_right;
		Node* suRL = suR->_left;
		int bf = suRL->_bf;
		RotateR(parent->_right);
		RotateL(parent);
		if (bf == -1)//在b插入
		{
			suR->_bf = 1;
			suRL->_bf = 0;
			parent->_bf = 0;
		}
		else if (bf == 1)//在c插入
		{
			suR->_bf = 0;
			suRL->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == 0)
		{
			suR->_bf = 0;
			suRL->_bf = 0;
			parent->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

五、判断AVL树

想要判断是否是AVL树有分为两步：
1：是否是二叉搜索树
用中序遍历能得到一个有序序列，说明是二叉搜索树。

void Inorder()
	{
		_Inorder(_root);
		cout << endl;
	}
	void _Inorder(Node* root)//中序遍历
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_kv.first << " ";
		_Inorder(root->_right);
	}

2：验证是否为平衡树
要满足下面两个条件

每个节点子树高度差的绝对值不超过1
节点的平衡因子是否计算正确
需要一下两个函数

    int height()
	{
		return _height(_root);
	}
	bool isblan()
	{
		return _isblan(_root);
	}
    int _height(Node* root)
	{
		if (root == nullptr)
			return 0;
		int lh = _height(root->_left);
		int rh = _height(root->_right);
		return lh > rh ? lh + 1 : rh + 1;
	}
	bool _isblan(Node* root)
	{
		if (root == nullptr)
			return true;

		int lh = _height(root->_left);
		int rh = _height(root->_right);
		if (rh - lh != root->_bf)
		{
			cout << root->_kv.first << ":bf异常" << endl;
			return false;
		}
		return abs(lh - rh) < 2 && _isblan(root->_left) && _isblan(root->_right);
	}

在判断函数中如果根节点为空返回真，接着计算左右子树的高度，调用高度函数，再判断平衡因子是否正确，不正确直接返回假，在返回时还要满足左右子树差的绝对值小于2，且root的左和右如果都是AVL树都为真，则该树一定是AVL树。

六、测试结果

测试函数及其结果

void Test1()
{
	int a[] = { 6,33,4,12,88,66,16,10,5 };
	AVLTRee<int, int>s;
	for (auto n : a)
	{
		s.Insert(make_pair(n, n));
		cout << n  <<":"<<s.isblan() << endl;
	}
	s.Inorder();
	cout <<"平衡正常："<< s.isblan() << endl;
	cout << "高度：" << s.height() << endl;


	cout << endl;
	srand(time(0));
	size_t N = 300000;
	AVLTRee<int, int> t;
	for (size_t i = 0; i < N; ++i)
	{
		size_t x = rand() + i;
		t.Insert(make_pair(x, x));
	}

	cout << "随机值构成的AVL树平衡正常：" << t.isblan() << endl;
	cout << "高度：" << t.height() << endl;
}

C++【实现AVL树】文章来源地址https://www.toymoban.com/news/detail-483925.html

七、源代码

(1) AVL_Tree.h

#pragma once
#include<utility>
#include<cassert>
#include<ctime>
#include<iostream>
using namespace std;
template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K,V>* _left;
	AVLTreeNode<K,V>* _right;
	AVLTreeNode<K,V>* _parent;
	pair<K, V>_kv;
	int _bf;
	AVLTreeNode(const pair<K,V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_kv(kv)
		,_bf(0)
	{}
};
template<class K,class V>
class AVLTRee
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool Insert(const std::pair<K,V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first > kv.first)
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_parent = parent;

		while (parent)
		{
			if (cur ==parent->_right)
			{
				parent->_bf++;
			}
			else
			{
				parent->_bf--;
			}

			if (parent->_bf == 1 || parent->_bf == -1)
			{
				parent = parent->_parent;//继续更
				cur = cur->_parent;
			}
			else if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == -1)
				{
					RotateR(parent);
				}
				else if (parent->_bf == -2 && cur->_bf ==1)
				{
					RotateLR(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1)
				{
					RotateRL(parent);

				}
				else
				{
					assert(false);
				}
				break;
			}
			else
			{
				assert(false);
			}
		}
		return true;
	}
	void Inorder()
	{
		_Inorder(_root);
		cout << endl;
	}
	int height()
	{
		return _height(_root);
	}
	bool isblan()
	{
		return _isblan(_root);
	}
private:
	void RotateL(Node* parent)//左单旋
	{
		Node* suR = parent->_right;//11的右孩子即22
		Node* suRL = suR->_left;//11的右孩子的左孩子即b
		Node* ppnode = parent->_parent;//维护父结点的父结点


		parent->_right = suRL;//11右孩子链接b
		if (suRL)//如果b不为空
			suRL->_parent = parent;//更新双亲结点


		suR->_left = parent;//22上提，左孩子链接11
		parent->_parent = suR;//更新双亲结点

		if (ppnode == nullptr)
		{
			_root = suR;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = suR;
			}
			else
			{
				ppnode->_right = suR;
			}
			suR->_parent = ppnode;
		}
		parent->_bf = suR->_bf = 0;//更新平衡因子

	}
	void RotateR(Node* parent)//右单旋
	{
		Node* suL = parent->_left;
		Node* suLR = suL->_right;

		parent->_left = suLR;
		if (suLR)
			suLR->_parent = parent;

		Node* ppnode = parent->_parent;

		suL->_right = parent;
		parent->_parent = suL;


		if (parent==_root)
		{
			_root = suL;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = suL;
			}
			else
			{
				ppnode->_right = suL;
			}
			suL->_parent = ppnode;
		}
		suL->_bf = parent->_bf = 0;
	}


	void RotateLR(Node* parent)//左右旋
	{
		Node* suL = parent->_left;
		Node* suLR = suL->_right;
		int bf = suLR->_bf;
		RotateL(parent->_left);
		RotateR(parent);
		if (bf == -1)//在b插入
		{
			parent->_bf = 1;
			suLR->_bf = 0;
			suL->_bf = 0;
		}
		else if (bf == 1)//在c插入
		{
			parent->_bf = 0;
			suLR->_bf = 0;
			suL->_bf = -1;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			suLR->_bf = 0;
			suL->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}


	void RotateRL(Node* parent)//右左旋
	{
		Node* suR = parent->_right;
		Node* suRL = suR->_left;
		int bf = suRL->_bf;
		RotateR(parent->_right);
		RotateL(parent);
		if (bf == -1)//在b插入
		{
			suR->_bf = 1;
			suRL->_bf = 0;
			parent->_bf = 0;
		}
		else if (bf == 1)//在c插入
		{
			suR->_bf = 0;
			suRL->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == 0)
		{
			suR->_bf = 0;
			suRL->_bf = 0;
			parent->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}
	void _Inorder(Node* root)//中序遍历
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_kv.first << " ";
		_Inorder(root->_right);
	}
	int _height(Node* root)
	{
		if (root == nullptr)
			return 0;
		int lh = _height(root->_left);
		int rh = _height(root->_right);
		return lh > rh ? lh + 1 : rh + 1;
	}
	bool _isblan(Node* root)
	{
		if (root == nullptr)
			return true;

		int lh = _height(root->_left);
		int rh = _height(root->_right);
		if (rh - lh != root->_bf)
		{
			cout << root->_kv.first << ":bf异常" << endl;
			return false;
		}
		return abs(lh - rh) < 2 && _isblan(root->_left) && _isblan(root->_right);
	}
private:
		Node* _root = nullptr;

};
void Test()
{
	int a[] = { 6,33,4,12,88,66,16,10,5 };
	AVLTRee<int, int>s;
	for (auto n : a)
	{
		s.Insert(make_pair(n, n));
		cout << n  <<":"<<s.isblan() << endl;
	}
	s.Inorder();
	cout <<"平衡正常："<< s.isblan() << endl;
	cout << "高度：" << s.height() << endl;

	cout << endl;
	srand(time(0));
	size_t N = 300000;
	AVLTRee<int, int> t;
	for (size_t i = 0; i < N; ++i)
	{
		size_t x = rand() + i;
		t.Insert(make_pair(x, x));
	}

	cout << "随机值构成的AVL树平衡正常：" << t.isblan() << endl;
	cout << "高度：" << t.height() << endl;
}

(2)test.cpp

#include"AVL_Tree.h"

int main()
{
	Test();
	return 0;
}

到了这里，关于C++【实现AVL树】的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！