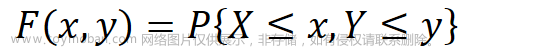目录
一、二维随机变量及其分布
1、二维随机变量
2、二维离散型随机变量(X,Y)
3、二维连续型随机变量(X,Y)
二、二维随机变量的独立性
三、二维均匀分布和二维正态分布
二维均匀分布
二维正态分布
四、二个随机变量函数Z=g(X,Y)的分布
X、Y均为离散型随机变量：
X、Y均为连续型随机变量：
X为离散型随机变量，Y为连续型随机变量：
Z=max{X,Y}的分布：转为小于等于号 P{max{X,Y}≤z}=P{X≤z,Y≤z}=P{X≤z}P{Y≤z}
Z=min{X,Y}的分布：转为大于号 P{min{X,Y}＞z}=P{X＞z,Y＞z}=P{X＞z}P{Y＞z}
必考：二维两个相互独立随机变量的条件概率密度；两个随机变量函数Z=g(X,Y)的分布；
一、二维随机变量及其分布
1、二维随机变量
●设X、Y是样本空间上的两个随机变量，则称向量(X,Y)为二维随机变量 /随机向量。
●二维随机变量(X,Y)的分布函数 /随机变量X和Y的联合分布函数：
●分布函数F(x,y)的性质：
●二维随机变量(X,Y)关于X和关于Y的边缘分布：
、
边缘分布和二维随机变量分布函数的关系：
●在条件Y=y下X的条件分布，记作：
在条件X=x下Y的条件分布，记作：
2、二维离散型随机变量(X,Y)
摘要：定义—概率分布(性质)—边缘分布(与概率分布的关系)—条件分布
●二维离散型随机变量的定义：满足条件
→称(X,Y)为二维离散型随机变量。
●二维概率分布/分布律：
也可用表格形式表示：
（习惯把x1、x2…竖着写，把y1、y2…横着写）
●二维概率分布pij的性质：
(概率大于0)
(概率之和等于1)
●(X,Y)关于X和关于Y的边缘分布：
边缘分布pi·和p·j与二维概率分布pij的关系：
pi·= P{X=xi} =pi1+pi2+……+pin； 确定X=xi，Y可取任意值，
p·j= P{Y=yj} =p1j+p2j+……+pnj 确定Y=Yj，X可取任意值，
（eg.确定X=x1,即i=1，p1·= P{X=1} =p11+p12+…+p1n）
（eg.确定Y=Y1,即j=1，p·1= P{Y=1} =p11+p21+…+pn1）
●若P{Y=yj＞0}，则有在条件Y=yj下X的条件分布：
3、二维连续型随机变量(X,Y)
摘要：定义—概率密度(性质)—边缘密度—条件密度
●二维连续型随机变量的定义：满足条件
→称(X,Y)为二维连续型随机变量。
●二维随机变量(X,Y)的概率密度 /随机变量X和Y的联合概率密度：f(x,y)
●概率密度f(x,y)的性质：
(概率密度大于0；
概率密度在-∞→+∞上积分等于1；
求(X,Y)落在某区域的概率，可以转化为在区域D上对概率密度的二重积分)
★概率密度的性质(3)每年必考！
●(X,Y)关于X和关于Y的边缘密度：
注意分别是对y积分和对x积分，被积函数是概率密度f(x,y)，积分区间是-∞→+∞
●若fY(y)＞0，则有在条件Y=y下X的条件密度：
★fY(y)＞0是条件密度fX|Y(x|y)成立的重要条件，经常考，要记牢！
同理，fX(x)＞0是条件密度fY|X(y|x)成立的重要条件。
小总结：连续型随机变量
★与分布函数F(x,y)相关的积分，积分区间一般为 -∞→x和 -∞→y
原因是
eg.一维随机变量X的分布函数F(x)的计算公式：
eg.二维随机变量(X,Y)的分布函数F(x,y)的计算公式：
★与概率密度f(x,y)相关的积分，积分区间一般为 -∞→+∞
原因是概率密度的性质，在-∞→+∞上对概率密度f(x,y)积分结果是1（全部的概率之和为1）
eg.一维随机变量X的概率密度f(x)的性质：
eg.二维随机变量(X,Y)的概率密度f(x,y)的性质：
★易记错的公式：
二维随机变量(X,Y)关于X的边缘密度：
和关于Y的边缘密度：
推导过程：
题型：求二维连续型随机变量(X,Y)的边缘密度
★(1)小题步骤：
1、由0＜y＜x＜1画分区图，找出概率密度不为0的区域(方便后续对概率密度的积分和确定积分区间)，和概率密度为0的区域
2、边缘密度公式——
3、等号写在哪——可以先模糊分区，最后再看端点加等号
关键分析：
由于边缘密度是对概率密度f(x,y)的定积分，而非零概率密度f(x,y)只在0＜y＜x＜1平面上取到。除此以外的部分概率密度f(x,y)都为0，自然边缘密度也都为0。
所以求边缘密度时只考虑在0＜y＜x＜1平面上的积分即可：
边缘密度fX(x)是对y积分，定积分上下限由y的取值范围确定
——由非零概率密度的区域0＜y＜x＜1推得0＜y＜x——y的积分区间为0→x
边缘密度fY(y)是对x积分，定积分上下限由x的取值范围确定
——由非零概率密度的区域0＜y＜x＜1推得y＜x＜1——x的积分区间为y→1
★(2)小题步骤：
1、先求出条件。由边缘密度fY(y)＞0时→ 0＜y＜1时，才有条件密度fX|Y(x|y)存在。
2、将计算出的边缘密度fY(y)和联合密度f(x,y)代入条件密度公式。这里注意题干中联合密度f(x,y)的分区：0＜y＜x＜1和其他，要照抄！
综合题：2013数三真题
第(1)题值得好好思考，思路很绕，一定要想清晰了！
二、二维随机变量的独立性
定义：随机变量X与Y相互独立：
离散型随机变量X与Y相互独立↔ 二维随机变量(X,Y)的概率分布=两个边缘分布相乘 pij=pi·p·j
连续型随机变量X与Y相互独立↔ 二维随机变量(X,Y)的联合密度=边缘密度相乘 f(x,y)=fX(x) fY(y)
题型：设X和Y相互独立，已知(X,Y)的联合分布部分数值，求剩余数值p21
关键：pij=pi·p·j，
(X,Y)关于X的边缘分布：p1·= P{X=1} =p11+p12+……+p1n 确定X=x1,即i=1,Y可取任意值
(X,Y)关于Y的边缘分布：p·1= P{Y=1} =p11+p21+……+pn1 确定Y=Y1,即j=1,X可取任意值
题型：已知离散型二维随机变量(X,Y)的联合分布，判断X与Y是否相互独立
★题型：给定分布，求概率P{X≥Y}
三、二维均匀分布和二维正态分布
二维均匀分布
定义
性质
★关键：
1、分区要准确！
(X,Y)的联合密度f(x,y)，根据x、y的取值情况分类
(X,Y)关于X的边缘密度fX(x)，根据x的取值分类
在X=x条件下Y的条件密度fY|X(y|x)，根据y的取值分类
2、积分上下限要准确！
边缘密度fX(x)是对y积分，定积分上下限由y的取值范围确定——由非零概率密度的区域x^2+y^2≤1推得y^2≤1-x^2——积分区间为：
→
。
3、对端点特别小心！
（2）求条件密度，条件密度fY|X(y|x)成立的条件是fX(x)＞0。查阅(1)中求的fX(x)，
可以推出fX(x)＞0时，-1＜x＜1。千万注意端点！这里取不到端点！
比较下面这个题，只能取到一边端点：
可以推出fY(y)＞0时，0 ≤ y＜2。这里只能取到一个端点！
二维正态分布
定义
性质
(X,Y)符合二维正态分布，则其边缘分布一定也是正态。
由 (X,Y)符合二维正态分布→X、Y都符合正态分布，
但是由X、Y都符合正态分布推不出 (X,Y)符合二维正态分布。
要再加一个条件，只有当X、Y都符合正态分布，且X与Y相互独立时，才可以推出(X,Y)符合二维正态分布。
四、二维随机变量函数Z=g(X,Y)的分布
X、Y均为离散型随机变量：
Z=g(X,Y)的分布律的求法与一维离散型类似。
X、Y均为连续型随机变量：
公式法：
X为离散型随机变量，Y为连续型随机变量：
Z=max{X,Y}的分布：转为小于等于号 P{max{X,Y}≤z}=P{X≤z,Y≤z}=P{X≤z}P{Y≤z}
（可以假设X≤Y，Z=max{X,Y}=Y，则max{X,Y}≤z即X＜Y≤z，写成X≤z且Y≤z）
文章来源：https://www.toymoban.com/news/detail-484171.html
Z=min{X,Y}的分布：转为大于号 P{min{X,Y}＞z}=P{X＞z,Y＞z}=P{X＞z}P{Y＞z}
（可以假设X≤Y，Z=min{X,Y}=X，则min{X,Y}＞z即Y＞X＞z，写成X＞z且Y＞z）
文章来源地址https://www.toymoban.com/news/detail-484171.html
到了这里，关于概率第三章 二维随机变量及其分布的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
