国密算法 SM2 公钥加密 数字签名 密钥交换 全网最高效的开源python代码

此前发布过SM2、SM3、SM4、ZUC等文章，以及开源的完整python代码。近些天看到一篇电子科大兰同学的硕士毕业论文（兰修文. ECC计算算法的优化及其在SM2实现中的运用[D]. 成都: 电子科技大学, 2019），文中采用预计算加速SM2椭圆曲线基点点乘，将这个思路用python代码实现后，实测比起原来的SM2又有4-5倍的提升。现把全网最快（也是功能实现最全）的SM2完整python代码分享出来（小弟口出狂言，若班门弄斧，还请大佬勿怪O(∩_∩)O）。愿大家同心协力推动国密算法普及，为国家网络安全添砖加瓦！

介绍其他国密算法的链接如下：

上一篇SM2：国密算法 SM2 公钥加密 非对称加密 数字签名 密钥协商 python实现完整代码_qq_43339242的博客-CSDN博客_python sm2

SM3：国密算法 SM3 消息摘要 杂凑算法 哈希函数 散列函数 python实现完整代码_qq_43339242的博客-CSDN博客_国密sm3

SM4：国密算法 SM4 对称加密 分组密码 python实现完整代码_qq_43339242的博客-CSDN博客_python国密算法库

ZUC：国密算法 ZUC流密码 祖冲之密码 python代码完整实现_qq_43339242的博客-CSDN博客_国密算法代码

对上述几个算法和实现不了解的，建议点进去看看。下面这篇文章是对上述的汇总：

国密算法 SM2公钥密码 SM3杂凑算法 SM4分组密码 python代码完整实现_qq_43339242的博客-CSDN博客_python sm2

所有代码托管在码云：hggm - 国密算法 SM2 SM3 SM4 python实现完整代码: 国密算法 SM2公钥密码 SM3杂凑算法 SM4分组密码 python代码完整实现 效率高于所有公开的python国密算法库 (gitee.com)

 SM2代码如下：

import random
import math
from hggm.SM3 import digest as sm3
from Crypto.PublicKey import ECC
from Crypto.Math.Numbers import Integer
from Crypto.Util._raw_api import VoidPointer, SmartPointer


# 转换为bytes，第二参数为字节数（可不填）
def to_byte(x, size=None):
    if isinstance(x, int):
        if size is None:  # 计算合适的字节数
            size = 0
            tmp = x >> 64
            while tmp:
                size += 8
                tmp >>= 64
            tmp = x >> (size << 3)
            while tmp:
                size += 1
                tmp >>= 8
        elif x >> (size << 3):  # 指定的字节数不够则截取低位
            x &= (1 << (size << 3)) - 1
        return x.to_bytes(size, byteorder='big')
    elif isinstance(x, str):
        x = x.encode()
        if size is not None and len(x) > size:  # 超过指定长度
            x = x[:size]  # 截取左侧字符
        return x
    elif isinstance(x, bytes):
        if size is not None and len(x) > size:  # 超过指定长度
            x = x[:size]  # 截取左侧字节
        return x
    elif isinstance(x, tuple):  # 坐标形式(x, y)
        if size is None:
            size = PARA_SIZE
        return to_byte(x[0], size) + to_byte(x[1], size)
    elif isinstance(x, Integer):
        return to_byte(int(x), size)
    elif isinstance(x, ECC.EccPoint):
        x, y = x.xy
        return to_byte(int(x), PARA_SIZE) + to_byte(int(y), PARA_SIZE)
    return bytes(x)


SM2_p = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
SM2_a = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
SM2_b = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
SM2_n = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
SM2_Gx = 0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
SM2_Gy = 0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0
PARA_SIZE = 32  # 参数长度（字节）
HASH_SIZE = 32  # sm3输出256位（32字节）
KEY_LEN = 128  # 默认密钥位数
SM2_w_l_1 = math.ceil(math.ceil(math.log(SM2_n, 2)) / 2) - 1  # w * 2


# 使用Crypto.PublicKey.ECC库生成SM2曲线
def gen_ECC_curve(p=SM2_p, b=SM2_b, n=SM2_n, Gx=SM2_Gx, Gy=SM2_Gy):
    # 如果未采用SM2标准规定的参数，则需要用pre_kG函数重新预计算kG，将输出矩阵作为全局变量kG_tuple，否则无法正确计算
    if 'sm2' not in ECC._curves or ECC._curves['sm2'].p != p:
        ec_context = VoidPointer()
        res = ECC._ec_lib.ec_ws_new_context(ec_context.address_of(), to_byte(p, PARA_SIZE), to_byte(b, PARA_SIZE),
                                            to_byte(n, PARA_SIZE), PARA_SIZE, random.getrandbits(64))
        if res:
            raise ImportError("Error %d initializing SM2 context" % res)
        context = SmartPointer(ec_context.get(), ECC._ec_lib.ec_free_context)
        ECC._curves['sm2'] = ECC._Curve(p, b, n, Gx, Gy, None, 256, p, context, '', '')


# 创建SM2点
def SM2_Point(xy):
    return ECC.EccPoint(xy[0], xy[1], 'sm2')


# 将字节转换为int
def to_int(byte):
    return int.from_bytes(byte, byteorder='big')


# 将列表元素转换为bytes并连接
def join_bytes(*data_list):
    return b''.join(to_byte(i) for i in data_list)


# 求最大公约数
def gcd(a, b):
    return a if b == 0 else gcd(b, a % b)


# 求乘法逆元过程中的辅助递归函数
def get_(a, b):
    if b == 0:
        return 1, 0
    x1, y1 = get_(b, a % b)
    x, y = y1, x1 - a // b * y1
    return x, y


# 求乘法逆元
def get_inverse(a, p):
    # return pow(a, p-2, p) # 效率较低、n倍点的时候两种计算方法结果会有不同
    if gcd(a, p) == 1:
        x, y = get_(a, p)
        return x % p
    return 1


# 密钥派生函数（从一个共享的秘密比特串中派生出密钥数据）
# SM2第3部分 5.4.3
# Z为bytes类型
# klen表示要获得的密钥数据的比特长度（8的倍数），int类型
# 输出为bytes类型
def KDF(Z, klen):
    ksize = klen >> 3
    K = bytearray()
    for ct in range(1, math.ceil(ksize / HASH_SIZE) + 1):
        K.extend(sm3(Z + to_byte(ct, 4)))
    return K[:ksize]


# 计算比特位数
def get_bit_num(x):
    if isinstance(x, int):
        num = 0
        tmp = x >> 64
        while tmp:
            num += 64
            tmp >>= 64
        tmp = x >> num >> 8
        while tmp:
            num += 8
            tmp >>= 8
        x >>= num
        while x:
            num += 1
            x >>= 1
        return num
    elif isinstance(x, str):
        return len(x.encode()) << 3
    elif isinstance(x, bytes):
        return len(x) << 3
    return 0


# 预计算kG（输出txt文本，内容为32行255列的椭圆曲线点矩阵）
def pre_kG():
    mySM2 = SM2()
    kG_point = [k * mySM2.G for k in range(1, 256)]
    with open('SM2_kG.txt', 'w') as f:
        print('[[' + ','.join(map(lambda p: '(0x%x,0x%x)' % p.xy, kG_point)) + '],', file=f)
        for i in range(31):
            for p in kG_point:
                p *= 256
            print('[' + ','.join(map(lambda p: '(0x%x,0x%x)' % p.xy, kG_point)) + '],\n', end='', file=f)
        print(']', file=f)


gen_ECC_curve()
# 计算好的kG点坐标（来自pre_kG函数输出的文本内容）
kG_tuple = []  # 这里本来不是空着的！PS：说我字数太多，所以[]里的大量内容就删掉了，可以在mian函数里运行pre_kG()，并把生成的文本内容复制进[]里面。当然，更建议直接去gitee下载完整源代码(●'◡'●)
# 将计算好的kG点坐标转换成SM2点
kG_points = [list(map(SM2_Point, plist)) for plist in kG_tuple]


# 采用预计算好的数据快速计算kG
def kG(k):
    P, i = None, 0
    while k:
        last_byte = k & 0xff
        if last_byte:
            if P is None:
                P = SM2_Point(kG_tuple[i][last_byte - 1])
            else:
                P += kG_points[i][last_byte - 1]
        k >>= 8
        i += 1
    return P


# SM2类继承ECC
class SM2:
    # 默认使用SM2推荐曲线参数
    def __init__(self, p=SM2_p, a=SM2_a, b=SM2_b, n=SM2_n, G=(SM2_Gx, SM2_Gy), h=1,  # 余因子h默认为1
                 ID=None, sk=None, pk=None, genkeypair=True):  # genkeypair表示是否自动生成公私钥对
        gen_ECC_curve(p, b, n, G[0], G[1])
        self.p, self.a, self.b, self.n, self.Gx, self.Gy, self.G, self.h = p, a, b, n, G[0], G[1], SM2_Point(G), h
        # 除曲线外的其他参数
        self.ID = ID if type(ID) in (int, str) else ''  # 身份ID（数字或字符串）
        if sk and pk:  # 已提供公私钥对
            try:  # 验证该公私钥对
                if kG(sk) == SM2_Point(pk):  # 通过验证，即使genkeypair=True也不会重新生成
                    self.sk, self.pk = sk, pk  # 私钥（int [1,n-2]），公钥（x, y）
                else:  # 不合格则生成
                    self.sk, self.pk = self.gen_keypair()
            except ValueError:  # 不在曲线上会报错，重新生成
                self.sk, self.pk = self.gen_keypair()
        elif genkeypair:  # 自动生成合格的公私钥对
            self.sk, self.pk = self.gen_keypair()

        # 预先计算用到的常数
        self.Z_tmp = to_byte(a) + to_byte(b) + to_byte(G[0]) + to_byte(G[1])  # Z值的中间部分
        if hasattr(self, 'sk'):  # 签名时
            self.d_1 = get_inverse(1 + self.sk, n)

    # 判断是否在椭圆曲线上
    def on_curve(self, p):
        try:
            return SM2_Point(p)  # 不报错则返回SM2_Point对象
        except ValueError:  # 报错说明不在曲线上
            return False

    # 生成密钥对
    # 返回值：d为私钥，P为公钥
    # SM2第1部分 6.1
    def gen_keypair(self, toTuple=True):
        d = random.randint(1, self.n - 2)
        P = kG(d)
        return d, tuple(map(int, P.xy)) if toTuple else P

    # 计算Z
    # SM2第2部分 5.5
    # ID为数字或字符串，P为公钥（不提供参数时返回自身Z值）
    def get_Z(self, ID=None, P=None):
        save = False
        if P is None:  # 不提供参数
            if hasattr(self, 'Z'):  # 再次计算，返回曾计算好的自身Z值
                return self.Z
            else:  # 首次计算自身Z值
                ID = self.ID
                P = self.pk
                save = True
        entlen = get_bit_num(ID)
        ENTL = to_byte(entlen, 2)
        Z = sm3(join_bytes(ENTL, ID, self.Z_tmp, P))
        if save:  # 保存自身Z值
            self.Z = Z
        return Z

    # 数字签名
    # SM2第2部分 6.1
    # 输入：待签名的消息M、随机数k（不填则自动生成）、输出类型（默认bytes）、对M是否hash（默认是）
    # 输出：r, s（int类型）或拼接后的bytes
    def sign(self, M, k=None, outbytes=True, dohash=True):
        if dohash:
            M_ = join_bytes(self.get_Z(), M)
            e = to_int(sm3(M_))
        else:
            e = to_int(to_byte(M))
        while True:
            if not k:
                k = random.randint(1, self.n - 1)
            x1 = int(kG(k).x)
            r = (e + x1) % self.n
            if r == 0 or r + k == self.n:
                k = 0
                continue
            s = self.d_1 * (k - r * self.sk) % self.n
            if s:
                break
            k = 0
        return to_byte((r, s), PARA_SIZE) if outbytes else (r, s)

    # 数字签名验证
    # SM2第2部分 7.1
    # 输入：收到的消息M′及其数字签名(r′, s′)、签名者的身份标识IDA及公钥PA、对M是否hash（默认是）
    # 输出：True or False
    def verify(self, M, sig, IDA, PA, dohash=True):
        PA_bytes = to_byte(PA)
        PA = self.on_curve(PA)
        if not PA:
            return False  # 对方公钥不在椭圆曲线上
        if isinstance(sig, bytes):
            r = to_int(sig[:PARA_SIZE])
            s = to_int(sig[PARA_SIZE:])
        else:
            r, s = sig
        if not 1 <= r <= self.n - 1 or not 1 <= s <= self.n - 1:
            return False
        if dohash:
            M_ = join_bytes(self.get_Z(IDA, PA_bytes), M)
            e = to_int(sm3(M_))
        else:
            e = to_int(to_byte(M))
        t = (r + s) % self.n
        if t == 0:
            return False
        PA *= t
        PA += kG(s)
        x1 = int(PA.x)
        # x1 = int((kG(s) + t * PA).x)
        R = (e + x1) % self.n
        return R == r

    # A 发起协商
    # SM2第3部分 6.1 A1-A3
    # 返回rA、RA
    def agreement_initiate(self):
        return self.gen_keypair()

    # B 响应协商（option=True时计算选项部分）
    # SM2第3部分 6.1 B1-B9
    def agreement_response(self, RA, PA, IDA, option=False, rB=None, RB=None, klen=None):
        # 参数准备
        PA_bytes = to_byte(PA)
        PA = self.on_curve(PA)
        if not PA:
            return False, '对方公钥不在椭圆曲线上'
        x1 = RA[0]
        RA = self.on_curve(RA)
        if not RA:
            return False, 'RA不在椭圆曲线上'

        if not hasattr(self, 'sk'):
            self.sk, self.pk = self.gen_keypair()
        ZA = self.get_Z(IDA, PA_bytes)
        ZB = self.get_Z()
        # B1-B7
        if not rB:
            rB, RB = self.gen_keypair()
        x2 = RB[0]
        x_2 = SM2_w_l_1 + (x2 & SM2_w_l_1 - 1)
        tB = (self.sk + x_2 * rB) % self.n
        x_1 = SM2_w_l_1 + (x1 & SM2_w_l_1 - 1)
        RA_bytes = to_byte(RA)
        RA *= x_1
        RA += PA
        RA *= self.h * tB
        xV, yV = RA.xy
        # V = (self.h * tB) * (x_1 * RA + PA)
        if (xV, yV) == (0, 0):
            return False, 'V是无穷远点'
        if not klen:
            klen = KEY_LEN
        KB = KDF(join_bytes((xV, yV), ZA, ZB), klen)
        if not option:
            return True, (RB, KB)
        # B8、B10（可选部分）
        tmp = join_bytes(yV, sm3(join_bytes(xV, ZA, ZB, RA_bytes, RB)))
        SB = sm3(join_bytes(2, tmp))
        S2 = sm3(join_bytes(3, tmp))
        return True, (RB, KB, SB, S2)

    # A 协商确认
    # SM2第3部分 6.1 A4-A10
    def agreement_confirm(self, rA, RA, RB, PB, IDB, SB=None, option=False, klen=None):
        # 参数准备
        PB_bytes = to_byte(PB)
        PB = self.on_curve(PB)
        if not PB:
            return False, '对方公钥不在椭圆曲线上'
        x1, x2 = RA[0], RB[0]
        RB = self.on_curve(RB)
        if not RB:
            return False, 'RB不在椭圆曲线上'
        if not hasattr(self, 'sk'):
            self.sk, self.pk = self.gen_keypair()
        ZA = self.get_Z()
        ZB = self.get_Z(IDB, PB_bytes)
        # A4-A8
        x_1 = SM2_w_l_1 + (x1 & SM2_w_l_1 - 1)
        tA = (self.sk + x_1 * rA) % self.n
        x_2 = SM2_w_l_1 + (x2 & SM2_w_l_1 - 1)
        RB_bytes = to_byte(RB)
        RB *= x_2
        RB += PB
        RB *= self.h * tA
        xU, yU = RB.xy
        # U = (self.h * tA) * (x_2 * RB + PB)
        if (xU, yU) == (0, 0):
            return False, 'U是无穷远点'
        if not klen:
            klen = KEY_LEN
        KA = KDF(join_bytes((xU, yU), ZA, ZB), klen)
        if not option or not SB:
            return True, KA
        # A9-A10（可选部分）
        tmp = join_bytes(yU, sm3(join_bytes(xU, ZA, ZB, RA, RB_bytes)))
        S1 = sm3(join_bytes(2, tmp))
        if S1 != SB:
            return False, 'S1 != SB'
        SA = sm3(join_bytes(3, tmp))
        return True, (KA, SA)

    # B 协商确认（可选部分）
    # SM2第3部分 6.1 B10
    def agreement_confirm2(self, S2, SA):
        if S2 != SA:
            return False, 'S2 != SA'
        return True, ''

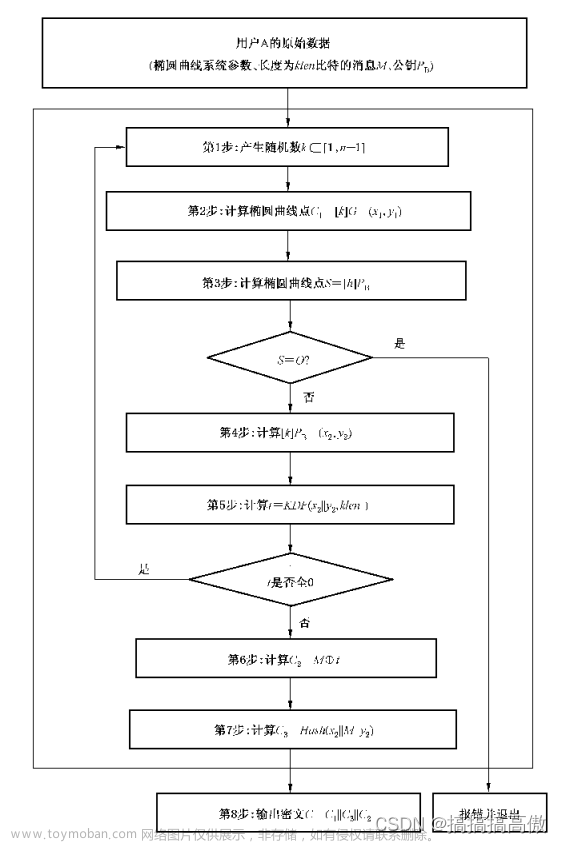
    # 加密
    # SM2第4部分 6.1
    # 输入：待加密的消息M（bytes或str类型）、对方的公钥PB、随机数k（不填则自动生成）
    # 输出(True, bytes类型密文)或(False, 错误信息)
    def encrypt(self, M, PB, k=None):
        PB = self.on_curve(PB)
        if not PB:
            return False, '对方公钥不在椭圆曲线上'
        M = to_byte(M)
        klen = get_bit_num(M)
        while True:
            if not k:
                k = random.randint(1, self.n - 1)
            PB *= k
            x2, y2 = PB.xy
            # x2, y2 = (k * PB).xy
            t = to_int(KDF(to_byte((x2, y2)), klen))
            if t:
                break
            k = 0  # 若t为全0比特串则继续循环
        C1 = to_byte(kG(k), PARA_SIZE)  # (x1, y1)
        C2 = to_byte(to_int(M) ^ t, klen >> 3)
        C3 = sm3(join_bytes(x2, M, y2))
        return True, join_bytes(C1, C2, C3)

    # 解密
    # SM2第4部分 7.1
    # 输入：密文C（bytes类型）
    # 输出(True, bytes类型明文)或(False, 错误信息)
    def decrypt(self, C):
        x1 = to_int(C[:PARA_SIZE])
        y1 = to_int(C[PARA_SIZE:PARA_SIZE << 1])
        C1 = self.on_curve((x1, y1))
        if not C1:
            return False, 'C1不满足椭圆曲线方程'
        C1 *= self.sk
        x2, y2 = C1.xy
        # x2, y2 = (self.sk * C1).xy
        klen = len(C) - (PARA_SIZE << 1) - HASH_SIZE << 3
        t = to_int(KDF(to_byte((x2, y2)), klen))
        if t == 0:
            return False, 't为全0比特串'
        C2 = C[PARA_SIZE << 1:-HASH_SIZE]
        M = to_byte(to_int(C2) ^ t, klen >> 3)
        u = sm3(join_bytes(x2, M, y2))
        C3 = C[-HASH_SIZE:]
        if u != C3:
            return False, 'u != C3'
        return True, M

注意：pycryptodome老版本没有int * EccPoint实现，新版本（3.14.1）缺SHA256和ARC4的链接库，我用的3.10.1版本是没问题的（pip install pycryptodome==3.10.1）

下面来看性能测试结果：

机器配置不高，处理器i3-10110U，不过差不了太多，相对速度还是有参考意义的。点乘测试都是针对椭圆曲线基点G进行，算法一、二、三是本实现的未加速版本（纯python实现，参考上一篇写SM2的文章），“加速后”指调用PyCryptodome库进行SM2椭圆曲线k·G运算。PyCryptodome库针对ECC的NIST P-256参数进行了数学优化，所以ECC计算k·G很快。但采用预计算以后，SM2的k·G已经追上ECC，且SM2的签名、验证比ECC签名、验证（即ECDSA算法）更快，可惜的是PyCryptodome库目前仍未实现ECC加密和解密。

用法请参考测试代码，需要的请下载完整代码，再次奉上链接：hggm - 国密算法 SM2 SM3 SM4 python实现完整代码: 国密算法 SM2公钥密码 SM3杂凑算法 SM4分组密码 python代码完整实现 效率高于所有公开的python国密算法库 (gitee.com)文章来源地址https://www.toymoban.com/news/detail-484281.html

到了这里，关于国密算法 SM2 公钥加密 数字签名 密钥交换 全网最高效的开源python代码的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！