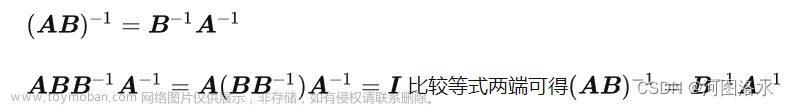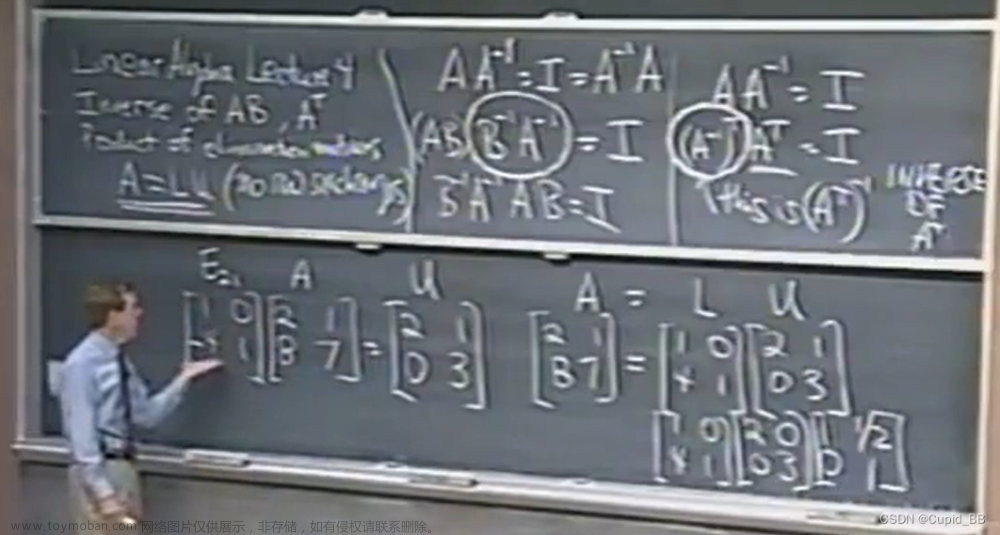数值分析——三角分解法（LU分解法）C++-Toy模板网

这篇具有很好参考价值的文章主要介绍了数值分析——三角分解法（LU分解法）C++。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

从例题着手,求解方程组：

10x1+20x2+20x3+50x4=200

50x1+40x2+10x3+10x4=250

30x1+10x2+40x3+20x4=210

20x1+40x2+40x3+40x4=340

根据方程组可以得到系数矩阵Aij[4][4], 通过矩阵A的元素进行LU分解；由Ax=b，从题干得到b[4]矩阵。现在已知了A、b矩阵，再通过LU分解法的递推公式计算出L U矩阵各个元素。

注意：（选用了最笨的办法）通过LU分解法的递推过程我们知道，要把系数矩阵A分解为L和U，需要先计算出U的第一行和L的第一列，接着计算出U的第二行L的第二列，继续U的第三行L的第三列......以此类推。整个递推的过程不是先计算出U的整个矩阵元素，再计算L的；两者是穿插进行的，直到所有行和列都陆续求出，得到最后完整的L[4][4], U[4][4]。

公式如下：

(1）U第一行，L第一列：u1i=a1i (i=0,1,2...n), li1=ai1/u11

(2)计算U的第r行，L的第r列元素：

Uri = Ari - Lrk*Uki, (i=r,r+1,...n);

Lir = ( Air - Lik*Ukr)/Urr, i=r+1,....n 且r != n；

(3)求解Ly=b， Ux=y 的计算公式：

y1=b1;

yi = bi - Lik*yk ,i=2,3,4...n;

xn=yn/Unn;

xi = ( yi - Uik*xk)/Uii , i=n-1,n-2,...1;

(根据上面公式编写代码)例题代码如下：


double Ai[4][4] = { 10,20,20,50,50,40,10,10,30,10,40,20,20,40,40,40 };  //Ai系数矩阵
double L[4][4] = { 0 }; //L初始化
double U[4][4] = { 0 }; //U初始化
double bi[4] = { 200,250,210,340 };  //b矩阵
double y[4] = { 0 };  //存放Ly=b 的结果y
double x[4] = { 0 }; //存放Ux=y 的最终结果x

void U1i_and_Li1( ) //计算U的第一行U1i，L的第一列Li1
{
    for (int i = 1; i <= 4; i++)
    {
        U[0][i-1] = Ai[0][i-1];
        L[i-1][0] = Ai[i-1][0] / U[0][0];
    }
}
//根据LU分解法递推公式分别计算U的某一行，L的某一列
void Uri(int m )  //形参m表示计算U的某一行
{
    double temp = 0.0;
    for (int r = 2; r <=m; r++)
    {
        for (int j = r; j <= 4; j++)
        {
            for (int k = 1; k <= r - 1; k++)
            {
                
                temp = temp + L[r - 1][k - 1] * U[k - 1][j - 1];
            }
            U[r-1][j-1] = Ai[r-1][j-1] - temp;
            temp = 0.0;
        }
    }
}
void Lir( int m) //m：L的某一列
{
    double temp = 0.0;
    for (int r = 2; r <= m; r++)
    {
        for (int i = r; i <= 4;i++)
        {
            for (int k = 1; k <= r - 1; k++)
            {
                temp = temp + L[i-1][k-1] * U[k-1][r-1];
            }
            L[i-1][r-1] = (Ai[i-1][r-1] - temp) / U[r-1][r-1];
            temp = 0.0;
        }
    }
}
void print(double a[4][4])  //打印结果
{
    for (int i = 0; i < 4; i++)
    {
        for (int j = 0; j < 4; j++)
        {
            cout << a[i][j] << " ";
            if ((i == 0 || i == 1 || i == 2 || i == 3) && j == 3)
                cout << endl;
        }
    }
}
void yi()  //计算yi
{
    double temp = 0;
    for (int i = 1; i <=4; i++)
    {
        if (i == 1)
            y[0] = bi[0];
        else 
        {
            for (int j = 1; j <=i - 1; j++)
            {
                temp = temp + L[i-1][j-1] * y[j-1];
            }
            y[i - 1] = bi[i - 1] - temp;
            temp = 0;
        }           
    }
}
void xi()  //计算最终结果xi
{
    double temp = 0;
    x[3] = y[3] / U[3][3];
    for (int i = 3; i >=1; i--)
    {
        for (int k = i + 1; k <=4; k++)
        {
            temp = temp + U[i - 1][k - 1] * x[k - 1];
        }
        x[i - 1] = (y[i - 1] - temp) / U[i - 1][i - 1];
        temp = 0;
    }
}

main函数和结果

int main()
{
    U1i_and_Li1();
    cout << "U 的第一行为：" << U[0][0] << " " << U[0][1] << " " << U[0][2] << " " << U[0][3] << endl;
    cout << "L 的第一列为：" << L[0][0] << " " << L[1][0] << " " << L[2][0] << " " << L[3][0] << endl;
    Uri(2);
    Lir(2);
    cout << "U 的第二行为：" << U[1][0] << " " << U[1][1] << " " << U[1][2] << " " << U[1][3] << endl;
    cout << "L 的第二列为：" << L[0][1] << " " << L[1][1] << " " << L[2][1] << " " << L[3][1] << endl;//l12,l22,l32,l42
    Uri(3);
    Lir(3);
    cout << "U 的第三行为：" << U[2][0] << " " << U[2][1] << " " << U[2][2] << " " << U[2][3] << endl;
    cout << "L 的第三列为：" << L[0][2] << " " << L[1][2] << " " << L[2][2] << " " << L[3][2] << endl;
    Uri(4);
    Lir(4);
    cout << "U 的第四行为：" << U[3][0] << " " << U[3][1] << " " << U[3][2] << " " << U[3][3] << endl;
    cout << "L 的第四列为：" << L[0][3] << " " << L[1][3] << " " << L[2][3] << " " << L[3][3] << endl;
    cout << "U矩阵表示为：" << endl;
    print(U);
    cout << "L矩阵表示为：" << endl;
    print(L);
    yi();
    cout << "由Ly=bi计算出y[4]为：" << y[0] << " " << y[1] << " " << y[2] << " " << y[3] << endl;
    xi();
    cout<< "由Ux=y计算出x[4]为：" << x[0] << " " << x[1] << " " << x[2] << " " << x[3] << endl;

    
    return 0;
}

数值分析——三角分解法（LU分解法）C++ 文章来源地址https://www.toymoban.com/news/detail-484526.html