ElGamal公钥密码算法(Python实现)-Toy模板网

这篇具有很好参考价值的文章主要介绍了ElGamal公钥密码算法(Python实现)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、实验目的（包括实验环境、实现目标等等）

1. 实验环境

Windows11
PyCharm2019.3.3 x64

2. 实现目标

通过编写代码实现EIGamal公钥密码算法，加深对EIGamal算法的理解，体会该算法在解决实际问题的价值；
将密码学和数学知识相联系，并灵活运用到密码学的设计方案中；
提高实践能力和逻辑思维能力。

二、方案设计（包括背景、原理、必要的公式、图表、算法步骤等等）

1. 背景

在密码学中，ElGamal加密算法是一个基于迪菲-赫尔曼密钥交换的非对称加密算法，它在1985年由塔希尔·盖莫尔提出。塔希尔·盖莫尔1955年出生于埃及开罗，密码学家。他是SSL的最初设计者，被称为SSL之父。
EIGamal公开密钥密码体制是基于有限域中离散对数问题的难解性。它所根据的原理是：求解离散对数是困难的，而其逆运算可以应用平方乘的方法有效地计算出来。在相应的群G中，指数函数是单向函数。所谓单向函数，它的意义就是在有限的算力之下如果你希望逆向去求的话是不可能做到的。

2. 离散对数困难问题

设g是模p的一个原根，任一整数h：

给定整数x，计算元素g^x ≡ h (mod ⁡p )很容易；
给定整数h，计算整数x，0 ≤ x ≤ P - 2，使得g^x ≡ h (mod ⁡p )非常困难。

3. EIGamal公钥加密算法

密钥产生过程：

随机选择一个大素数 p 以及两个小于 p 的随机数 g 和 x（ g 是 p 的一个原根）；
计算 y ≡ g^x mod⁡ p；
以(y， g，p)作为公开密钥，x作为私密密钥。

加密过程：

设欲加密明文消息为 M；
随机选取一个与 p - 1 互素的整数k；
计算C₁ ≡ g^k mod ⁡p，C₂ ≡ y^k M mod⁡ p；
密文为C = (C₁，C₂）。

解密过程：
ElGamal公钥密码算法(Python实现)

4. 实验准备

强素数：在这里，定义强素数为：若p为一个素数，且q=2p+1也是一个素数，则称q是一个强素数。
欧拉函数：在数论中，对正整数n，欧拉函数是小于或等于n的正整数中与n互质的数的数目。此函数以其首名研究者欧拉命名，它又称为∅函数（由高斯命名）。
原根：原根是一种数学符号，设m是正整数，a是整数，若a模m的阶等于∅(m)，则称a为模m的一个原根。（其中∅(m)表示m的欧拉函数，即a^∅(m)≡1(mod ⁡m )）

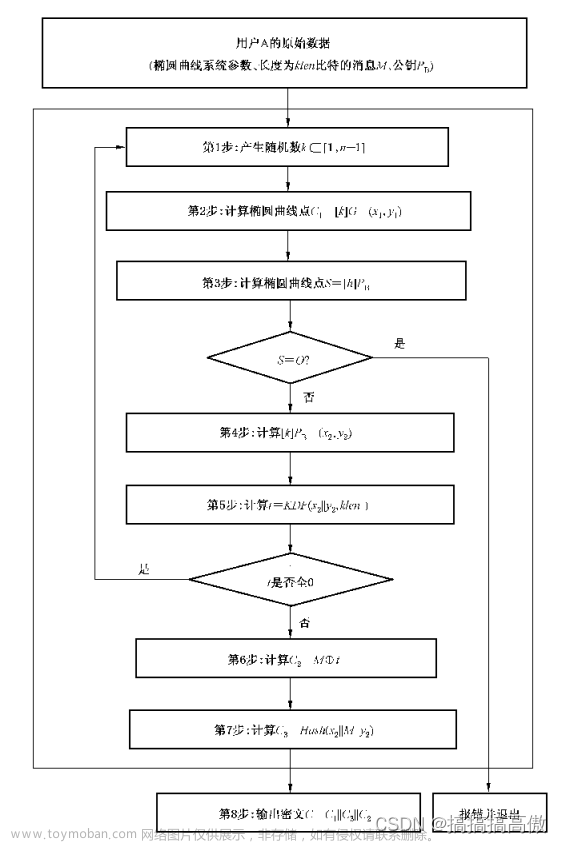
三、方案实现（包括算法流程图、主要函数的介绍、算法实现的主要代码等等）

1. 流程图

ElGamal公钥密码算法(Python实现)

2. 主要函数

sys.setrecursionlimit(10000)：递归深度设置为10000，防止递归深度不够
def fastExpMod()：快速取模幂
def primitive_element()：生成原根
def e_gcd()
def encrypt()：Bob加密
def decrypt()：Alice解密

3. Python代码

from random import randint
import sympy
import sys

sys.setrecursionlimit(10000)


def fastExpMod(a, e, m):
    a = a % m
    res = 1
    while e != 0:
        if e & 1:
            res = (res * a) % m
        e >>= 1
        a = (a * a) % m
    return res


def primitive_element(p, q):
    while True:
        g = randint(2, p - 2)
        if fastExpMod(g, 2, p) != 1 and fastExpMod(g, q, p) != 1:
            return g


def e_gcd(a, b):
    if b == 0:
        return a, 1, 0
    g, x, y = e_gcd(b, a % b)
    return g, y, x - a // b * y


def encrypt(p, g, y, m):
    while True:
        k = randint(2, p - 2)
        if e_gcd(k, p - 1)[0]:
            break
    c1 = fastExpMod(g, k, p)
    c2 = (m * fastExpMod(y, k, p)) % p
    return c1, c2


def decrypt(c1, c2, p, a):
    v = fastExpMod(c1, a, p)
    v_1 = e_gcd(v, p)[1]
    m_d = c2 * v_1 % p
    return m_d


def main():
	# 这里的路径：读者自己电脑测试文件存放的正确路径
    m = int(open("F:\密码学实验\secret2.txt").readline())
    while True:
        q = sympy.randprime(10 ** 149, 10 ** 150 / 2 - 1)
        if sympy.isprime(q):
            p = 2 * q + 1
            if len(str(p)) == 150 and sympy.isprime(p):
                break
    g = primitive_element(p, q)
    a = randint(2, p - 2)
    y = fastExpMod(g, a, p)
    c1, c2 = encrypt(p, g, y, m)
    m_d = decrypt(c1, c2, p, a)

    if m == m_d:
        print("解密结果与明文相同！解密正确！")
    else:
        print("解密结果与明文不同！解密不正确！")
    return m, p, g, y, c1, c2, m_d


if __name__ == '__main__':
    print("m = %d\nALice的公钥：\np = %d\ng = %d\ng^a = %d\n密文(C1, C2) = (%d,\n%d)\n明文m = %d"
          % main())

四、数据分析(包括算法测试数据的分析，运行结果截图等等)

1. secret0

9327260388393076415930260479153046010064951650867096323260782111903507989221223155043829435161867334962529353992935468294479465522637777146290777

运行结果：
ElGamal公钥密码算法(Python实现)

2. secret1

268934047525129207430358090155831774406988263017537886266459743124401877032780923870438637078936998897356703572131607069480172048042746

运行结果：
ElGamal公钥密码算法(Python实现)

3. secret2

53440167287330489793805749223384077746504290188205908391653679301485458082326877556058376895190593105090632340942230488922602

运行结果：
ElGamal公钥密码算法(Python实现)

五、思考与总结

请简述什么是本原根，给定素数P，如何求其本原根？文章来源地址https://www.toymoban.com/news/detail-485411.html

本原根：原根是一种数学符号，设m是正整数，a是整数，若a模m的阶等于∅(m)，则称a为模m的一个原根。（其中∅(m)表示m的欧拉函数，即a^∅(m)≡1(mod m )）。
生成本原根的方法有很多，比如遍历、判断等；本实验选取的方法为：随机生成一个素数p，若p为一个素数，且q = 2p + 1也是一个素数，则称q是一个强素数。接着随机生成一个整数g (1 < g < P - 1)，若g² ≠ 1，且g^q ≠ 1，则g是大素数p的一个本原根。

到了这里，关于ElGamal公钥密码算法(Python实现)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！