1.二部图
(1)二部图(偶图):
若能将无向图G=<V,E>的顶点集V划分成两个不相交的非空子集V1和V2,使得G中任 何一条边的两个端点一个属于V1,另一个属于V2 ,则称G为二部图,V1,V2称为互补顶点子集,此时可将G记成G=<V1,V2,E>.
(2)完全二部图:
若V1中每一个顶点与V2中每一个顶点均有且仅有一条边相关联,则称二部图G为完全二部图(或完全偶图).当|V1|=n,|V2l=m时,完全二部图G记为Kn,m.
上面那个图就是完全二部图
(3)二部图的判定:一个无向图是二部图当且仅当G中没有长度为奇数的回路
2.匹配
(1)匹配:设G=<V,E>为无向图,M含于E,若M中任意两条边均不相邻,则称M为G中的匹配
(2)极大匹配:在M中再加人任何1条边就都不是匹配.
(3)最大匹配: 边数最多的匹配称为最大 匹配
(4)匹配数:最大匹配中边的条数.记为βG),简记为β1.
(5)饱和点:设M为G中一个匹配,v∈V(G),若存在M中的边与v关联,则称v为M饱和点,否则v为M非饱和点.实际上就是匹配中的顶点
(6)完美匹配:若G中每个顶点都是M饱和点(M中的顶点),称M为完美匹配.如下图:
(7)完备匹配:设G=〈V1,V2,E〉为一个二部图,|V1|≤|V2l ,M为G中一个最大匹配,若|M|=|V1l,则称M为G中V1,到V2的完备匹配.当|V1|=lV2|时,完备匹配是完美匹配.
(8)判断完备匹配:
1)Hall定理:设二部图G=<V,V2 ,E>,|V1|≤|V2l,G中存在从V1到V2的完备匹配当且仅当V1中任意k个顶点至少邻接V2中的k个顶点.(充分必要条件)
2)t定理:设二部图G=<V1,V2,E>,如果存在t>0使得:
V1中每个顶点至少关联t条边;
V2中每个顶点至多关联t条边.
则G中存在V1到V2的完备匹配.(充分条件)
3.欧拉图
(1)欧拉回路(欧拉通路):经过图(无向图或有向图)中每条边一次且仅一次并且行遍图中每个顶点的回路(通路)
(2)欧拉图:欧拉回路的图
(3)欧拉通路和欧拉回路判定
首要条件:图是连通图
1)欧拉回路判定:
无向图:所有顶点度数都是偶数(没有奇度顶点)
有向图:每个顶点的出度等于入度
2)欧拉通路判定:
无向图:有且只有两个顶点度数为奇数,这两个顶点为始点和终点,其他顶点度都是偶数
有向图:只有两个顶点入度不等于出度,其他顶点入度等于出度,且一个端点入度数比出度大1作为终点,另一个端点入度数比出度小1作为起点.

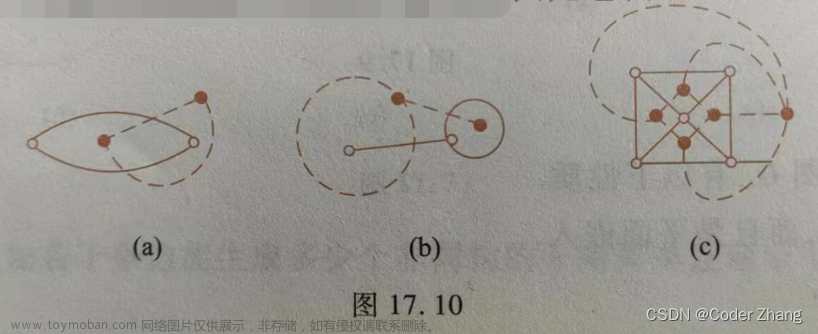
解:(a)都是奇度顶点,无欧拉通路和欧拉回路,不是欧拉图
(b)恰有两个奇度顶点,有欧拉通路,无欧拉回路,是半欧拉图
(C)无奇度顶点,有欧拉回路,是欧拉图
(d)只有一个出度对于入度的的顶点,无欧拉回路和通路不是欧拉图
(e)恰有两个出度不等于入度且一个点出度大于入度一个入度大于出度的点,所以存在欧拉通路不存在欧拉回路,是半欧拉图
(f)每个顶点的出度都大于入度,有欧拉回路,是欧拉图
4.哈密顿图(顶点n>=3的完全图都是)
(1)哈密顿回路(哈密顿通路):经过图中每个顶点一次且仅一次的回路(通路)
(2)哈密顿图:存在哈密顿回路的图
(3)哈密顿图判定:
1)必要条件:设无向图G=<V,E>是哈密顿图,V1是V的任意的非空子集,则p(G-V1)≤|V1l
推论:设无向图G=<V,E>中有哈密顿通路,V1是V的任意的非空子集,则p(G-V1)≤|V1l+1.
使用其逆否命题来判断该图不是哈密顿图
例:
解:V1={a,b,c,d,e,f,g},p(G-V1)=9>|V1|+1=8不存在哈密顿通路
(2)充分条件:
设G是n(n3)阶无向简单图,如果G中任何一对不相邻的顶点的度数之和都大于等于n—1,则G中存在哈密顿通路.
如果G中任何一对不相邻的顶点的度数之和都大于等于n,则G是哈密顿图.
在n(n≥2)阶有向图D中, 如果所有有向边均用无向边代替, 所得无向图中含生成子图Kn, 则有向图D中存在哈密顿通路。
推论:n(n≥3)阶有向完全图为哈密顿图
以下内容了解即可
5.竞赛图:
任意两个顶点之间恰好有一条有向边.竞赛图一定有哈密顿通路
6:(1)格雷码:
把所有n位0-1串排成一个序列,相邻的两个以及最后一个和第一个之间只有一位不同,这样的序列称作格雷码.当n=3时,000,100,101,111,110,010,011,001是一个格雷码
(2)寻找格雷码:
构造一个n维立方体图,它有2”个顶点,每个顶点表示一个n位串,两个顶点之间有一条边当且仅当它们的n位串仅相差一位.
7.平面图
(1)平面图:如果能将图G除顶点外边不相交地画在平面上,则称G是平面图
这个画出的无边相交的图称作G的平面嵌入. 没有平面嵌入的图称作非平面图
(2)设G是一个平面嵌入
1)G的面: 由G的边将平面划分成的每一个区域
2)无限面(外部面): 面积无限的面, 用R0表示
3)有限面(内部面): 面积有限的面, 用R1, R2,…, Rk表示
4)面Ri的边界: 包围Ri的所有边构成的回路
5)面Ri的次数: Ri边界的长度,用deg(Ri)表示
(3)平面图的性质:平面图各面的次数之和等于边数的2倍。
8.极大平面图
(1)极大平面图:若G是简单平面图, 并且在任意两个不相邻的顶点之间加一条新边所得图为非平面图,则称G为极大平面图
(2)极小非平面图:若G是非平面图, 并且任意删除一条边所得图都是平面图, 则称G为极小非平面图
(3)极大平面图性质:
1)极大平面图必连通.
2)阶数大于等于3的极大平面图中不可能有割点和桥.
3)任何n(n>=4)阶极大平面图G均有最大度δ(G)>=3.
(4)极大平面图判断
n(n>=3)阶简单平面图是极大平面图当且仅当它连通且每个面的次数都为3.
10.(1)同胚:(a)消去2度顶点w,(b)插入2度顶点w,如果G1和G2同构经过反复(a)(b)操作后同构,则称G1与G2同胚,例( c)(d)同胚


(2)收缩:删除边(u ,v),用新的顶点w(可以用u或v充当w)取代u,v,并使w和除(u , v)外所有与u、v关联的边关联,称这个变换为收缩边(u, v).如果G可以通过若干次收缩边得到G,则称G可收缩到G2.
在这里插入图片描述文章来源:https://www.toymoban.com/news/detail-485887.html
(3)库拉图斯基定理
1)一个图是平面图当且仅当它不含与K5同胚的子图,也不含与K3,3同胚的子图.
2)一个图是平面图当且仅当它没有可收缩到K5的子图也没有可收缩到K3,3的子图.
11.四色定理:任何平面图都是4-可着色的文章来源地址https://www.toymoban.com/news/detail-485887.html
到了这里,关于【离散数学期复习系列】五、一些特殊的图的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!