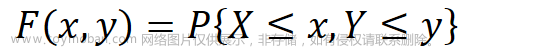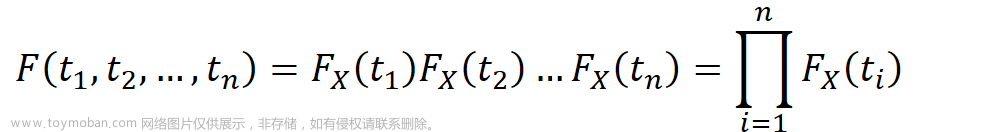视频
古典概型
常见的古典概型题目分为：
- 有放回
- 无放回
有放回
对于有放回的题目，一般可以这样做：
举个例子，如题：
则它们的答案是：
1.
C
4
4
∗
（
2
5
）
4
C_{4}^{4} *（\frac{2}{5}）^4
C44∗（52）4
2.
C
4
2
∗
（
2
5
）
2
∗
C
2
2
∗
（
1
5
）
2
C_{4}^{2} *（\frac{2}{5}）^2*C_{2}^{2} *（\frac{1}{5}）^2
C42∗（52）2∗C22∗（51）2
3.
C
4
2
∗
（
2
5
）
2
∗
C
2
1
∗
（
1
5
）
∗
C
1
1
∗
（
1
5
）
C_{4}^{2} *（\frac{2}{5}）^2*C_{2}^{1} *（\frac{1}{5}）*C_{1}^{1} *（\frac{1}{5}）
C42∗（52）2∗C21∗（51）∗C11∗（51）
无放回
一般是：摸东西，但是不会只摸一个，问同时摸到某些东西的概率（无放回）。
一般做法：
如题：
则它们的答案是：
1.
（
C
5
3
C
10
3
）
（\frac{C_{5}^{3} } {C_{10}^{3} }）
（C103C53）
2.
（
C
5
2
∗
C
3
1
C
10
3
）
（\frac{C_{5}^{2}*{C_{3}^{1}} } {C_{10}^{3} }）
（C103C52∗C31）
3.
（
C
5
1
∗
C
3
1
∗
C
2
1
C
10
3
）
（\frac{C_{5}^{1}*{C_{3}^{1}} *{C_{2}^{1}}} {C_{10}^{3} }）
（C103C51∗C31∗C21）
一个小练习：
显然是无放回的。
答案：
（ C 100 2 ∗ C 300 1 C 700 3 ） （\frac{C_{100}^{2}*{C_{300}^{1}} } {C_{700}^{3} }） （C7003C1002∗C3001）
几何概型
通过画图的方求概率的题型。常见的几何概型的题目如下：文章来源：https://www.toymoban.com/news/detail-486976.html
- 有范围
- 给若干数
- 求数在范围内的概率
做法：画图。
步骤：
例题1与答案：
例题2：
答案：
例3与例4：
例3答案：
例4答案：
文章来源地址https://www.toymoban.com/news/detail-486976.html
到了这里，关于【概率论与数理统计】猴博士 笔记 p1-p2 古典概型、几何概型的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
