目录
题目描述
解题思路
DP初始化
DP最终条件
DP初始条件
题目限制条件
总代码
题目描述

解题思路
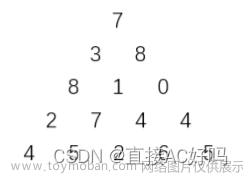
首先映入我们眼帘的就是一个三角形,加求路径和最大,类似于找最短路径的题,很明显是一个二维数组的动态规划问题,对于动态规划问题我们只需要找好最终条件,初始条件(也就是特殊条件),当然还要题目限制的条件既可求解。
DP初始化
我们需要两个二维数组,一个是array数组存放的是题目输入进来的三角形数据,第二个数组是dp数组存放的是到每一步的最大路径和。
n=int(input())
array=[list(map(int,input().strip().split())) for j in range(n)]
dp=[[0 for i in range(n)]for j in range(n)]DP最终条件
排开特殊的状态也就是初始状态,一个数无非从左上来或者从右上来,取其中两个最大的和该点相加这就是最终条件
dp[i][j]=max(dp[i-1][j-1]+array[i][j],dp[i-1][j]+array[i][j])DP初始条件
我们观察此题一共有三个初始状态需要我们初始化:
1.当这个数是第一个数时,我们就直接把值赋值给它
if i==j==0:
dp[i][j]=array[0][0]2.当这个数在第一列时,那么他的值只可能从右上来,我们需要把上一排右上的值赋值给他
elif j==0:
dp[i][j]=dp[i-1][j]+array[i][j]3.当这个数是这一排最后一个数时,由题目可知也就是i=j时,这个数的值只可能从左上来,我们需要把上一排左上的值赋值给他
elif i==j:
dp[i][j]=dp[i-1][j-1]+array[i][j]题目限制条件
通过以上的DP我们算出了每个点的最大路径值,那么题目要求我们向左和向右的差值不能超过1。我们通过观察可以发现:
1.当到奇数行时要满足向左向右差值不能是1,这个值必然是最中间的值
if n&1:
print(dp[n-1][n//2])2.当到偶数行时要满足向左向右差值不能是1,这个值必然是最中间两个值的一个文章来源:https://www.toymoban.com/news/detail-487063.html
else:
print(max(dp[n-1][n//2-1],dp[n-1][n//2]))其实就是从奇数行(第一行)的最中间出发,然后出发到第二行,到第三行奇数行的时候为了平衡不管第二行是什么结果都会跑到第三行正中间,平衡后 就又可以左右都走,跑到了偶数行的中间两个。文章来源地址https://www.toymoban.com/news/detail-487063.html
总代码
n=int(input())
array=[list(map(int,input().strip().split())) for j in range(n)]
dp=[[0 for i in range(n)]for j in range(n)]
for i in range(n):
for j in range(i+1):
if i==j==0:
dp[i][j]=array[0][0]
elif j==0:
dp[i][j]=dp[i-1][j]+array[i][j]
elif i==j:
dp[i][j]=dp[i-1][j-1]+array[i][j]
else:
dp[i][j]=max(dp[i-1][j-1]+array[i][j],dp[i-1][j]+array[i][j])
if n&1:
print(dp[n-1][n//2])
else:
print(max(dp[n-1][n//2-1],dp[n-1][n//2]))
到了这里,关于数字三角形-蓝桥杯真题动态规划PYTHON解法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!