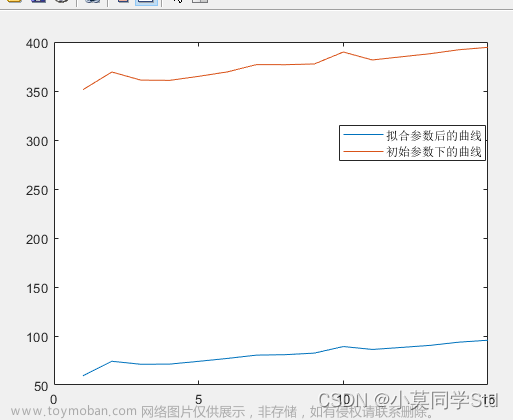
线性拟合的斜率和截距的不确定性
利用熟悉的Excel绘图功能,可以根据距离-高程散点数据拟合线性趋势线,如图1显示(河流阶地地形数据)。趋势线按如下方式插入:右击图表上的数据,添加趋势线,在图表上显示方程和 R 2 R^2 R2值。然而,趋势线函数并没有给出与线性拟合的斜率和截距相关的方差值。获得斜率和截距选定的置信区间(例如95%置信区间)对于精确测量断层变形量与滑动速率十分重要。因此,我们需要计算斜率与截距的方差值。Excel的LINESET函数提供这种统计测量。下文介绍了使用LINEST的基本步骤与原理(Morrison, 2014)。
图1. 拔河高度随距离的函数。利用Excel的趋势线特性对数据进行拟合;直线方程和拟合系数R2值如图所示。
Excel数组函数LINEST
使用MS Excel的 LINEST函数 进行最小二乘计算。对于图1所示数据,应用LINEST步骤如下:
- 选择一个5行2列的空白范围(总共10个单元格)来存放函数的输出值;我们选择B1:C5,如图2所示。
- 点击公式,然后 “插入函数”。
- 在 “插入函数” 窗口中,类别选择 “Statistical”,选择函数 “LINEST”,然后单击确定。
- 选择y和x数据范围;对于Const,输入TRUE(TRUE=计算非0截距);对于Stats,也选择TRUE (TRUE=返回误差统计值);单击OK。
- 通过选择输入字段中的公式并按键盘 CTRL-SHIFT-ENTER,指定LINEST是一个数组函数。选定的10个输出单元格将填充与图2和图3中标记的匹配相关的统计信息,下文进行讨论。

图2. 按照文本中的说明,填充LINEST的函数参数,如图所示。点击OK之后,还有最后一个重要的步骤:突出显示函数调用=LINEST(B9:B1493, A9:A1493, true, true)并同时按CTRL-SHIFT-ENTER。
图3. 在指定LINEST是一个数组函数之后,10个单元格B1:C5显示误差统计信息。这些统计值的含义见文本。
LINEST结果的含义
LINEST执行最小二乘运算求解最佳拟合直线的斜率和截距(图4,Wikipedia, 2014b)。最佳线性拟合对应拟合直线和数据之间的平方和误差值最小。通常,最小二乘计算中,假设x值没有误差(图4),详细推导见文献(Montgomery and Runger, 2011; McCuen, 1985),本文仅作简短讨论。
图4. 因变量y的平均值是参数(斜率和截距)和变量x的线性组合。通常最小二乘算法假设数据的x值不存在误差,响应变量y的残差计算为 y i − y ^ i y_i-\widehat{y}_i yi−y
i,即点与直线之间的垂直距离(左图)。若x中的误差也存在,点和直线之间的最短距离是垂直距离,如右图所示。各因变量 y i y_i yi的误差是互不相关的,即每个 y i y_i yi之间不存在协方差。
值(xi, yi)是n个数据对的集合,我们希望拟合一条线; y ˉ ≡ ( ∑ i = 1 n y i ) / n \bar{y}≡(\sum_{i=1}^n y_i )/n yˉ≡(∑i=1nyi)/n是yi的均值,并且线性拟合是 y ^ ( x ) = m ^ x + b ^ \widehat{y}(x)=\widehat{m}x+\widehat{b} y (x)=m x+b ,为了解释Excel返回的误差统计值,首先定义三个平方和: S S y y SS_{yy} SSyy, S S E SS_E SSE, 和 S S R SS_R SSR
总平方和 S S T SS_T SST= S S y y SS_{yy} SSyy= ∑ i = 1 n ( y i − y ˉ ) 2 \sum\limits_{i=1}^n(y_i-\bar{y})^2 i=1∑n(yi−yˉ)2 (1)
误差平方和 S S E SS_E SSE≡ ∑ i = 1 n ( y i − y ^ ) 2 \sum\limits_{i=1}^n(y_i-\widehat{y})^2 i=1∑n(yi−y
)2 (2)
回归平方和 S S R SS_R SSR≡ S S T − S S E SS_T-SS_E SST−SSE (3)文章来源:https://www.toymoban.com/news/detail-487176.html
S S y y SS_{yy} SSyy是数据 y i y_i yi与均值 y ^ \widehat{y} y
之间误差平方和; S S E SS_E SSE是数据 y i y_i yi和拟合值 y ^ ( x ) \widehat{y}(x) y
(x)= m ^ x + b ^ \widehat{m}x+\widehat{b} m
x+b
之间的误差平方和; S S R SS_R SSR是二者之差,代表总平方和中可以用线性模型值解释的部分。在最小二乘计算中,目标是找到最小化的 S S E SS_E SSE,计算过程还涉及到两个平方和公式:
S S x x SS_{xx} SSxx≡ ∑ i = 1 n ( x i − x ˉ ) 2 \sum\limits_{i=1}^n(x_i-\bar{x})^2 i=1∑n(xi−xˉ)2 (4)
S S x y SS_{xy} SSxy≡ ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) \sum\limits_{i=1}^n(x_i-\bar{x})(y_i-\bar{y}) i=1∑n(xi−xˉ)(y文章来源地址https://www.toymoban.com/news/detail-487176.html
到了这里,关于利用Excel的LINEST计算线性拟合的斜率和截距的不确定性的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!