算法Day38 | 动态规划，509. 斐波那契数， 70. 爬楼梯， 746. 使用最小花费爬楼梯-Toy模板网

这篇具有很好参考价值的文章主要介绍了算法Day38 | 动态规划，509. 斐波那契数， 70. 爬楼梯， 746. 使用最小花费爬楼梯。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

动态规划

动态规划是一种解决问题的算法思想。它通常用于优化问题，其中要求找到一个最优解或最大化（最小化）某个目标函数。

动态规划的核心思想是将问题分解成更小的子问题，并通过存储子问题的解来避免重复计算。这样，可以通过解决子问题来构建原始问题的解。动态规划通常适用于具有重叠子问题和最优子结构特性的问题。

动态规划的一般步骤如下：

确定dp数组以及下标的含义
确定递推公式
dp数组初始化
确定遍历顺序
举例推导dp数组

动态规划与数学归纳法的异同：

	动态规划	数学归纳法
目的	解决优化问题	证明命题的正确性
解决方法	将问题划分为子问题，通过存储子问题的解避免重复计算	将问题归纳到更小的情况进行证明
焦点	求解问题的过程	问题的正确性证明
应用领域	计算机科学、运筹学、经济学等	数学、逻辑学等
相同之处	都通过将问题分解为更小的部分来解决	都需要基于已知情况来推导出新的结论

509. 斐波那契数

题目链接：509. 斐波那契数

class Solution {
public:
    int fib(int n) {
        vector<int> dp{0, 1};
        dp.resize(n + 1);
        for (int i = 2; i < n + 1; ++i) {
            dp[i] = dp[i - 2] + dp[i - 1];
        }
        return dp.back();
    }
};

根据公式 $F (n) = F (n - 1) + F (n - 2)$ ，本题其实只需要维护两个变量就可以求出，称之为滚动数组

class Solution {
public:
    int fib(int n) {
        if (n <= 1) return n;
        int val1 = 0, val2 = 1;
        while(n-- >= 2) {
            int sum = val2 + val1;
            val1 = val2;
            val2 = sum;
        }
        return val2;
    }
};

动态规划中的滚动数组是一种空间优化技巧，通常用于解决空间复杂度较高的动态规划问题。滚动数组通过使用一维数组来代替二维数组的一部分或全部，从而减少空间复杂度。在动态规划的递推过程中，每一个状态只与之前的一个或几个状态有关，因此只需要用一维数组来保存这些状态的值，而不需要用二维数组保存所有状态值。当计算完当前状态后，可以覆盖掉前面的状态值，从而实现滚动数组的效果。

例如，求解斐波那契数列的动态规划实现通常使用滚动数组。在计算当前状态值时，只需要用两个变量来分别保存前两个状态的值，而不需要使用一个数组来保存所有状态值。每次计算完当前状态值后，将保存前一个状态值的变量的值更新为当前状态值，将保存前两个状态值的变量的值更新为保存前一个状态值的变量的值，即可实现滚动数组。

使用滚动数组可以大大减少动态规划算法的空间复杂度，但同时也可能会影响程序的可读性和可维护性，因为使用滚动数组通常需要更多的变量和复杂的变量更新操作。因此，在使用滚动数组时需要权衡空间和时间复杂度与程序可读性和可维护性之间的关系，选择最优的算法实现方式。

70. 爬楼梯

题目链接：70. 爬楼梯
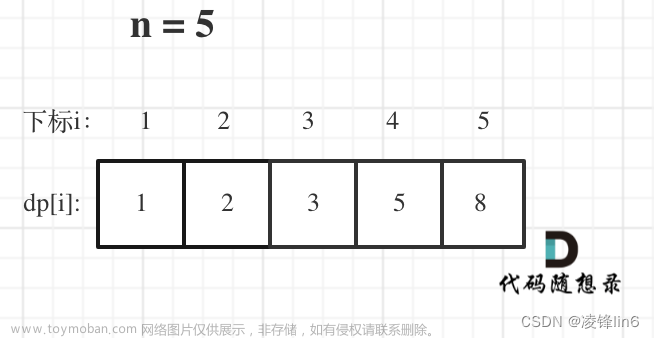
1个台阶，有1种方法；2个台阶，有2种方法；3个台阶，有1+2种方法。

3个台阶就是1个台阶和2个台阶的总和。为什么？因为题目就让迈1个或2个台阶，因此到3阶，从1阶迈两步，从2阶迈一步，因此是1阶和2阶的总和。这就是将问题分解成更小的子问题，并通过存储子问题的解来避免重复计算

同理，4个台阶，通过3阶迈一步，2阶迈两步，有2+3种方法。
… …

dp 数组的含义：到达第 i 阶，有 dp[i] 种方法
递推公式：dp[i] = dp[i -1] + dp[i - 2]
初始化：dp[1] = 1; dp[2] = 2（dp[0]没有意义，但是为了满足递推公式，可以初始化为1）
遍历顺序：从前向后

class Solution {
public:
    int climbStairs(int n) {
        vector<int> dp{1, 1, 2};
        dp.resize(n + 1);
        for (int i = 3; i < n + 1; ++i) {
            dp[i] = dp[i - 2] + dp[i - 1];
        }
        return dp.back();
    }
};

当然，因为是斐波那契数列，也可以维护只两个变量来完成。

746. 使用最小花费爬楼梯

题目链接：746. 使用最小花费爬楼梯
dp 数组的含义：到达第 i 阶，所需要的花费为 dp[i]
递推公式：dp[i] = min(dp[i -1] + cost[i - 1], dp[i - 2] + cost[i - 2])
初始化：根据题意可知，dp[0] = 0; dp[1] = 0
遍历顺序：从前向后文章来源地址https://www.toymoban.com/news/detail-487664.html

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        vector<int> dp{0, 0};
        dp.resize(cost.size() + 1);
        for (int i = 2; i < cost.size() + 1; ++i) {
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp.back();
    }
};