多层感知机与深度学习算法概述
读研之前那会儿我们曾纠结于机器学习、深度学习、神经网络这些概念的异同。现在看来深度学习这一算法竟然容易让人和他的爸爸机器学习搞混…可见深度学习技术的影响力之大。深度学习,作为机器学习家族中目前最有价值的一种算法,正在悄悄改变着世界以及我们生活。
本本我们就要搞清楚【深度学习】到底是什么?有哪些技术细节?
1. 多层感知机

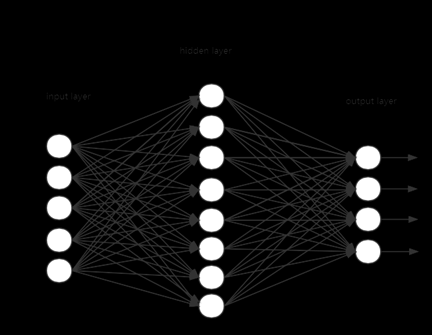
图1 多层感知机拓扑结构
对于单层神经网络,人们担心它表达能力不足,于是参照仿生结构,想到了带有隐层的神经网络。所有隐藏都可以看成对输入的再次表示,最后的输出层则是一个单层线性神经网络。
2. 从多层感知机到深度学习
2.0 多层感知机的局限
H = X W 1 + b 1 O = H W 2 + b 2 (2-1) H=XW_1+b_1\\ O=HW_2+b_2\tag{2-1} H=XW1+b1O=HW2+b2(2-1)
这是具有单隐层神经网络的输入输出关系。w1、w2、b1、b2分别是隐层、输出层的权重和偏置。这看似参数量比单层神经网络要多,模型的拟合能力应该更好?但如果稍加推导可以发现:
O
=
(
(
X
W
1
+
b
1
)
W
2
)
+
b
2
=
X
W
1
W
2
+
b
1
W
2
+
b
2
=
X
W
3
+
b
3
(2-2)
O=((XW_1+b_1)W_2)+b_2\\ =XW_1W_2+b_1W_2+b_2\\ =XW_3+b_3\tag{2-2}
O=((XW1+b1)W2)+b2=XW1W2+b1W2+b2=XW3+b3(2-2)
简单的推导可以发现,没有引入非线性单元的多层感知机,就是一个“多层感知鸡”(鸡肋的鸡)。完全可以等效成单层神经网络啊!
那怎么办呢?引入非线性单元啊:每层的输出经过非线性函数后再传给下一层,就没法通过(2-2)的推导转化成单层了。多层感知机+非线性单元——这就是几乎所有深度学习的最基本结构。
2.1 层
- **输入层:**输入层神经元个数必须和输入特征数一致。
- **隐藏层:**隐藏层神经元个数一般多于输入层神经元个数,以起到升维映射的作用,可以更好的提取特征。
- **输出层:**神经元个数应该等于预期输出数目。还可以根据任务不同加上一些激活函数来限制网络输出的值(比如分类问题的softmax)。一般来说,输出层为【全连接层】,全连接层意味着所有的神经元都将由权重建立连接。而输入层和隐藏层一般不是全连接层(比如对于CV这种输入特征非常多的任务)。
当然了,【层,layer】这一概念肯定不止上面3个,但上面3个是所有神经网络共有的层。深度学习发展历程中还出现了一些有关“层”的trick,比如最经典的 卷积层、归一化层、Dropout层等等。。。这些将在深度学习trick中统一梳理。
2.2 块
2.3 非线性单元(激活函数)
激活函数有很多种,但比较常用的就这三种,从此搞明白激活函数的概念。
-
ReLU(Rectified linear unit):
这是目前最常见的激活函数,可能99%的情况都用这个,因为它能很好的克服反向传播梯度消失的问题。
R e L U ( x ) = m a x ( x , 0 ) (2-3) ReLU(x)=max(x,0)\tag{2-3} ReLU(x)=max(x,0)(2-3)
图2 ReLU函数图像它的导数什么样很好想象吧,就不画了。有一个小小的问题,x=0时不可导啊?没关系 不差这一个点了,因为权重不可能恒等于0,所以我们令x=0处的导数为0即可。
-
Sigmod:
在ReLU出现之前,这是最常用的激活函数,但是因为其计算有些复杂,影响训练测试速度;更重要的是其会导致梯度消失问题,导致网络层数无法加深。所以现在几乎不咋用这个了。
s i g m o d ( x ) = 1 1 + e − x (2-4) sigmod(x)=\frac{1}{1+e^{-x}}\tag{2-4} sigmod(x)=1+e−x1(2-4)
图3 Sigmod函数图像导数什么样也很好想象吧…就是中间大,两头小,类似正态分布…
-
Tanh:
这就是Sigmod函数的极端版,更类似阶跃函数(其实阶跃函数才是最具有仿生意义的)。
T a n h ( x ) = 1 − e − 2 x 1 + e − 2 x (2-5) Tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}\tag{2-5} Tanh(x)=1+e−2x1−e−2x(2-5)
图4 Tanh函数图像
导数就。。更尖了。
这里没提softmax,softmax看上去是一种非线性单元,但其实可以证明还是起到线性的作用,之前讲过,这里省略了。
2.4 数据集
当你要从零开始做一个预测任务时(可能是CV/NLP,可能是det、seg、ocr…),**你最应该关注的并不是作为算法核心的模型,而是数据。**巧妇难为无米之炊,再nb的模型,没有高质量、高数量的数据,也不会有更好的效果,反而有更差的效果。数据与模型的关系在[2.5]节中讨论。
对于成熟的深度学习搭建框架,一般会把数据集分成三类:
训练集(train dataset)、验证集(validation dataset)、测试集(test dataset)。
然而为了省事,验证集和测试集一般设置成一样的,这一点影响不大。但是你最好应该分清楚训练、验证、测试这3个过程,特别是验证和测试的区别:
验证:在训练过程中,每n个epoch跑一次验证集的数据,进行一次验证,用来观察当前选取模型(网络+超参数)的拟合能力和泛化能力。
测试:在完全完成训练之后,最终跑一次测试集数据,用来评估模型训练的最终结果。
2.4 训练与推理
训练和推理是深度学习(也是大部分机器学习算法)最基本的两个动作。
- 训练过程:一次正向传播(forwad)+一次反向传播(backward),为一次迭代(iteration);一次迭代使用的数据叫一个批量(batch);对训练集全部数据完整迭代过一次,称为一个周期(epoch)。
- 推理过程:比训练过程简单很多,一般来说推理的批量为1,即一次只推理一个数据。推理过程只包括一次正向传播,不需要记录梯度。
以下过程我们按只有一个隐藏层的多层感知机来推导。
网络模型:输入x,标签y,隐藏层前具有一个激活函数φ,输入层参数W1,隐藏层参数W2,输出o,损失函数l,正则项s。
2.4.1 正向传播
沿网络输入,逐层计算到网络输出、目标函数。
-
输入层输出:
z = W 1 x (2-6) z=W_1x\tag{2-6} z=W1x(2-6) -
激活函数输出:
h = φ ( z ) (2-7) h=φ(z)\tag{2-7} h=φ(z)(2-7) -
输出层输出:
o = W 2 h (2-8) o=W_2h\tag{2-8} o=W2h(2-8) -
损失:
L = l ( o , y ) (2-9) L=l(o,y)\tag{2-9} L=l(o,y)(2-9) -
正则项:
s = ω 2 ( ∣ ∣ W 1 ∣ ∣ 2 2 + ∣ ∣ W 2 ∣ ∣ 2 2 ) (2-10) s=\frac{\omega}{2}(||W_1||_2^2+||W_2||_2^2)\tag{2-10} s=2ω(∣∣W1∣∣22+∣∣W2∣∣22)(2-10) -
目标函数:
J = L + s (2-11) J=L+s\tag{2-11} J=L+s(2-11)
2.4.2 反向传播
反向传播需要计算目标函数关于各个层参数的梯度(偏导),由于多层感知机的拓扑结构,只能从目标函数到损失函数、到输出、到隐藏层。。。到输入,从后向前地计算各层的梯度。
-
参照(2-11)、(2-9)计算目标函数关于输出o的梯度:
∂ J ∂ o = p r o d ( ∂ J ∂ L , ∂ L ∂ o ) = ∂ L ∂ o (2-12) \frac{\partial J}{\partial o}=prod(\frac{\partial J}{\partial L},\frac{\partial L}{\partial o})=\frac{\partial L}{\partial o}\tag{2-12} ∂o∂J=prod(∂L∂J,∂o∂L)=∂o∂L(2-12)
J对于L的偏导明显是1,不解释吧… -
参照(2-10)计算正则项关于W1、W2的梯度:
∂ s ∂ W 1 = ω W 1 ∂ s ∂ W 2 = ω W 2 (2-13) \frac{\partial s}{\partial W_1}=\omega W_1\\ \frac{\partial s}{\partial W_2}=\omega W_2\tag{2-13} ∂W1∂s=ωW1∂W2∂s=ωW2(2-13) -
参照(2-11)、(2-8)计算目标函数关于隐层参数W2的梯度:
∂ J ∂ W 2 = p r o d ( ∂ J ∂ o , ∂ o ∂ W 2 ) + p r o d ( ∂ J ∂ s , ∂ s ∂ W 2 ) = ∂ L ∂ o h T + ω W 2 (2-14) \frac{\partial J}{\partial W_2}=prod(\frac{\partial J}{\partial o},\frac{\partial o}{\partial W_2})+prod(\frac{\partial J}{\partial s},\frac{\partial s}{\partial W_2})\\ =\frac{\partial L}{\partial o}h^T+\omega W_2\tag{2-14} ∂W2∂J=prod(∂o∂J,∂W2∂o)+prod(∂s∂J,∂W2∂s)=∂o∂LhT+ωW2(2-14)
同样,J对s的偏导是1 -
参照(2-8)计算目标函数关于隐藏变量h的梯度:
∂ J ∂ h = p r o d ( ∂ J ∂ o , ∂ o ∂ h ) = W 2 T ∂ L ∂ o (2-15) \frac{\partial J}{\partial h}=prod(\frac{\partial J}{\partial o},\frac{\partial o}{\partial h})=W_2^T\frac{\partial L}{\partial o}\tag{2-15} ∂h∂J=prod(∂o∂J,∂h∂o)=W2T∂o∂L(2-15) -
参照(2-7)反向穿过激活函数φ计算目标函数关于输入层输出z的梯度:
∂ J ∂ z = p r o d ( ∂ J ∂ h , ∂ h ∂ z ) = ∂ J ∂ h ⋅ φ ′ ( z ) (2-16) \frac{\partial J}{\partial z}=prod(\frac{\partial J}{\partial h},\frac{\partial h}{\partial z})=\frac{\partial J}{\partial h}\cdotφ^{'}(z)\tag{2-16} ∂z∂J=prod(∂h∂J,∂z∂h)=∂h∂J⋅φ′(z)(2-16)
这里的’.'是向量内积,因为激活函数是逐元素计算的,这里计算梯度要用向量内积。
-
最后,我们可以得出目标函数关于W1的梯度:
∂ J ∂ W 1 = p r o d ( ∂ J ∂ z , ∂ z ∂ W 1 ) + p r o d ( ∂ J ∂ s , ∂ s ∂ W 1 ) = ∂ J ∂ z x T + ω W 1 (2-17) \frac{\partial J}{\partial W_1}=prod(\frac{\partial J}{\partial z},\frac{\partial z}{\partial W_1})+prod(\frac{\partial J}{\partial s},\frac{\partial s}{\partial W_1})\\ =\frac{\partial J}{\partial z}x^T+\omega W_1\tag{2-17} ∂W1∂J=prod(∂z∂J,∂W1∂z)+prod(∂s∂J,∂W1∂s)=∂z∂JxT+ωW1(2-17) -
至此我们就求出了该多层感知机的所有权重梯度。按(2-14)、(2-17)引用优化器策略更新权重即可。
2.5 过拟合与欠拟合
过拟合与欠拟合表示模型在经过训练后的状态,但这种状态与数据情况、模型情况都紧密相关。
图5 过拟合与欠拟合
这两种状态直观上可由训练损失与泛化损失界定;背后由模型复杂度和数据规模决定。
直观上:
当泛化损失大于训练损失时,我们就可以称模型此时在该数据集上处于过拟合状态;
当训练损失处于较大时,我们可以称模型此时在数据集上处于欠拟合状态。
背后:
当模型复杂度(参数规模)越高、数据集规模越小,越容易处于过拟合状态。
当模型复杂度(参数规模)越低、数据集规模越大,越容易处于欠拟合状态。
关于此的一些讨论:
- 所以你现在知道当你的模型处于欠拟合和过拟合时应该怎么做了吧,是调整模型,还是调整数据?
- 欠拟合一定是一件坏事,宁可过拟合也不要欠拟合。
- 换个角度看过拟合,模型过拟合了,那一定效果就很差吗?不一定,可能只是泛化损失略高于训练损失,但泛化损失并没有太大,模型也能有非常好的效果(只是离最佳状态稍微过火了一点点)。因此,宁可略微过拟合,也不要欠拟合。
- 过拟合一定是坏事吗?表面看上去是的,模型泛化能力不佳,应用时可能就会出问题。但!万一有一种数据集,可以保证它的分布和隐含的数据总体分布一致呢?比如NLP领域的预训练,就是要在预训练数据上让模型达到过拟合状态,因为人类的文字和语言意义就是那些,学完了就了事了。但CV领域并不是这样,似乎很难有某种数据集能和世间图像数据的总体分布达到一致,这也是CV领域预训练技术的难题之一。
总结
本文试图:
- 从多层感知机的问题出发,引出深度学习算法。
- 对深度学习算法的基本组成介绍明白。
- 深度学习实现效果的总体评价方法做一个介绍。
诚然,时至今日 深度学习是一个较大的计算机科学领域了。深度学习领域又可以分为若干小领域。
按应用场景分:CV、NLP、数据分析…(每个应用场景又分出好多细分领域…)
按算法分:CV的卷积神经网络、NLP的transformer/注意力机制、强化学习…(每个算法也有若干细分算法,适用于各种应用场景)文章来源:https://www.toymoban.com/news/detail-487831.html
那么多场景,那么多算法;可能对于每个深度学习从业个体而言 不论是做科研还是工程,第一件要做的事情就是搞清楚自己的细分应用场景+适用的几种算法。以此为中心,向下深挖、向周围辐射,加自己在深度学习领域的认识深度和广度,更好地体会深度学习对我们生活的影响和改变。文章来源地址https://www.toymoban.com/news/detail-487831.html
到了这里,关于多层感知机与深度学习算法概述的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!